In this article, we have explained how to insert an element at the bottom of Stack using standard stack operations like push and pop. We have covered two approaches: iterative and recursive.

Table of Contents:

1. Problem Statement / Introduction
2. Naive approach
3. Recursive approach
4. Application of stack & adding elements at bottom

Problem Statement / Introduction

Stack is a linear data structure. It follows LIFO (Last in First Out) order. It has two major operations push and pop:

• Push: Adds an element at the top of the stack.
• Pop: Removes the top element from the stack.

In this problem, we need to insert an element at the bottom of the stack. We will use these approaches to solve this problem-

1. Naive approach
2. Recursive approach

Add elements at the top of the stack:

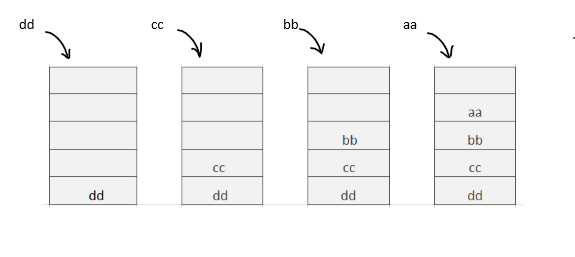
Add elements at the bottom of stack:

Here, we may implement a method (insertAtBottom) to add an element at the bottom of the stack because the stack push method only adds elements at the top of the stack.

Naive approach

In the naive approach, we have used a temporary stack to store the popped elements.

Steps:

1. Call the insertAtBottom function. Push the elements in a temporary stack (tmpStack) and pop the elements from the stack until the stack becomes empty.
2. Push element N into the stack.
3. Push the previously stored elements in the stack and pop the elements from the temporary stack until the temporary stack becomes empty.
4. Return the stack.

/**
 * insert an element N at the bottom of stack
 */

import java.util.Stack;

public class InsertAtBottomIterative {
    public static Stack<String> insertAtBottom(Stack<String> stack, String N) {
        //create a temporary stack
        Stack<String> tmpStack = new Stack<String>();

        //stores the top elements in tmpStack
        while (!stack.empty()) {
            String val = stack.peek();
            tmpStack.push(val);
            stack.pop();
        }

        //adds new element N
        stack.push(N);

        //adds previously stored elements
        while (!tmpStack.empty()) {
            String val = tmpStack.peek();
            tmpStack.pop();
            stack.push(val);
        }
        return stack;
    }

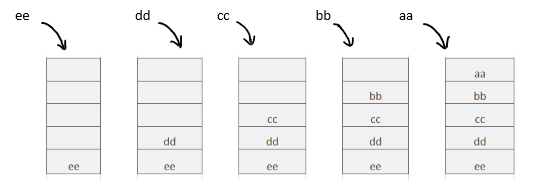
    public static void main(String[] args) {
        Stack<String> stack = new Stack<String>();
        String N = "ee";
        stack.push("dd");
        stack.push("cc");
        stack.push("bb");
        stack.push("aa");

        stack = insertAtBottom(stack, N);

        while (!stack.empty()) {
            System.out.print(stack.peek() + " ");
            stack.pop();
        }
        System.out.println();
    }
}

Output:

aa bb cc dd ee

Time Complexity: O(n)
Auxiliary Space: O(n)

Push(), pop() and peek() take O(1) time. Here, each loop takes O(n) time. We have used an extra stack so it takes O(n) auxiliary space.

Recursive approach

In the recursive approach, we will use recursion to insert an element at bottom of Stack. Recursion allows a function to call itself. The insertAtBottom function takes two parameters a stack and the element. The return type of the function is void. In this implementation, we don't need any explicit temporary stack.

Steps:

1. Call the insertAtBottom function. For each element in the stack, pop the element, store it in a variable and call the function insertAtBottom.
2. When the stack becomes empty, push the element N into the stack and exit the method.
3. After each recursive call in insertAtBottom, push the previously stored element in the stack and exit the method.

After calling the insertAtBottom function:

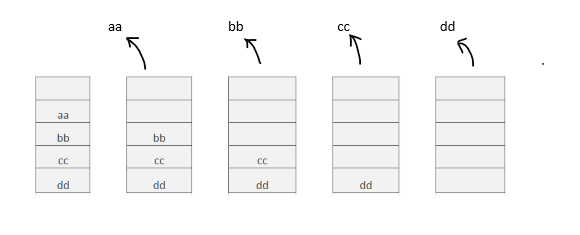
Inserting new and all stored elements when the stack becomes empty:

public static void insertAtBottom(Stack<String> stack, String N) {

        //if stack is empty
        if (stack.empty()) {
            //insert N into stack and return
            stack.push(N);
            return;
        }

        /**
         * store top element of stack in tmp
         * pop the top element
         * call the insertAtBottom function
         * push previous element
         */
        String tmp = stack.peek();
        stack.pop();
        insertAtBottom(stack, N);
        stack.push(tmp);
        return;
    }

Time Complexity: O(n)
Space Complexity: O(n)

In the recursive approach, we have used implicit stack through recursion. insertAtBottom function is called n times recursively. It will take O(n) space and O(n) time.

Application of stack & adding elements at bottom

Common applications of Stack are as follows:

1. In backtracking algorithms.
2. In memory management.
3. Expression handling.

In specific cases, there may be a requirement that element needs to be added at the bottom of stack. Our approaches are useful in this situation. In many cases, the stack has a support for adding an element at the bottom directly in O(1) time but when using Stack from standard library, we need to provide our custom implementation.

With this article at OpenGenus, you must have the complete idea of inserting elements at the bottom of the stack.