
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article we will explore the time and space complexity of a popular sorting algorithm called Bubble Sort. We will also explore an optimization of this algorithm and it's complexity.
Table of Contents:
- Introduction to Bubble sort
- Time Complexity Analysis
- Worst Case Time Complexity
- Best Case Time Complexity
- Average Case Time Complexity
- Space Complexity
- Comparison with other Sorting Algorithms
Introduction to Bubble sort
Bubble sort is an algorithm that sequentially steps through a list of items and swaps items if they aren't in the correct order till the list is sorted.
Here's an example of the sorting technique visualized:
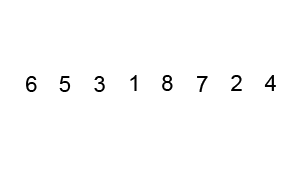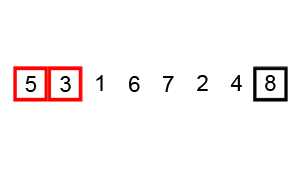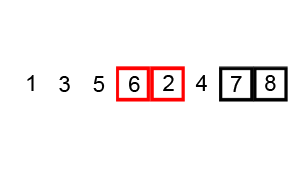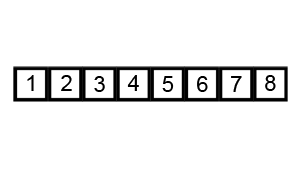
As the visual shows, the elements seem to bubble up to their correct positions in the list and thus the name of bubble sort. It is also referred to as comparison or sinking sort.
Pseudocode
1. procedure bubbleSort(A : list of sortable items)
2. n := length(A)
3. for i := 0 to n-1 inclusive do
4. for j := 0 to n-i-1 inclusive do
5. // the elements aren't in the right order
6. if A[j] > A[j+1] then
7. // swap the elements
8. swap(A[j], A[j+1])
9. end if
10. end for
11. end for
12. end procedure
Time Complexity Analysis
In this unoptimised version the run time complexity is Θ(N^2). This applies to all the cases including the worst, best and average cases because even if the array is already sorted the algorithm doesn't check that at any point and runs through all iterations. Although the number of swaps would differ in each case.
The number of times the inner loop runs
$= \sum_{j=1}^{N-i-1} 1 \tag{2}$
$= (N - i) \tag{1}$
The number of times the outer loop runs
$= \sum_{i=1}^{N-1} \sum_{j=1}^{N-i-1} 1 = \sum_{i=1}^{N-1} N - i \tag{3}$
$= \frac{N * (N-1)}{2} \tag{4}$
Optimization
We add an additional check that breaks out of the outer loop if no swaps occur in the inner loop.
Implementation
1. void bubbleSort(vector<int> &v) {
2. int n = v.size();
3. bool swapped = true;
4. int i, j;
5. for(i = 0; i < n-1; ++i) {
6. swapped = false;
7. for(j = 0; j < n-i-1; ++j) {
8. if(v[j] > v[j+1]) {
9. // elements are out of order
10. swap(v[j], v[j+1]);
11. // remember a swap occurred
12. swapped = true;
13. }
14. }
15. // check if array is sorted
16. if(swapped == false) break;
17. }
18. }
Complexity
Now we can analyze the:
- Time complexity T(N)
- Number of swaps S(N)
- Number of comparisons C(N)
for each case. This is done by observing the number of times the lines 8-13 run in each case.
T(N) = S(N) + C(N)
Time Complexity = Number of Swaps + Number of Comparisons
The relation are as follows:
T(N) = T(N-1) + N
C(N) = C(N-1) + (N-1)
S(N) depends on the distribution of elements.
Worst Case Time Complexity
Θ(N^2) is the Worst Case Time Complexity of Bubble Sort.
This is the case when the array is reversely sort i.e. in descending order but we require ascending order or ascending order when descending order is needed.
The number of swaps of two elements is equal to the number of comparisons in this case as every element is out of place.
$T(N) = C(N) = S(N) = \frac{N*(N-1)}{2}$, from equation 2 and 4
Therefore, in the worst case:
- Number of Comparisons: O(N^2) time
- Number of swaps: O(N^2) time
Best Case Time Complexity
Θ(N) is the Best Case Time Complexity of Bubble Sort.
This case occurs when the given array is already sorted.
For the algorithm to realise this, only one walk through of the array is required during which no swaps occur (lines 9-13) and the swapped variable (false) indicates that the array is already sorted.
$T(N) = C(N) = N$
$S(N) = 0$
Therefore, in the best case:
- Number of Comparisons: N = O(N) time
- Number of swaps: 0 = O(1) time
Average Case Time Complexity
Θ(N^2) is the Average Case Time Complexity of Bubble Sort.
The number of comparisons is constant in Bubble Sort so in average case, there is O(N^2) comparisons. This is because irrespective of the arrangement of elements, the number of comparisons C(N) is same.
For the number of swaps, consider the following points:
- If an element is in index I1 but it should be in index I2, then it will take a minimum of I2-I1 swaps to bring the element to the correct position.
- An element E will be at a distance of I3 from its position in sorted array. Maximum value of I3 will be N-1 for the edge elements and it will be N/2 for the elements at the middle.
- The sum of maximum difference in position across all elements will be:
(N-1) + (N-3) + (N-5) ... + 0 + ... + (N-3) + (N-1)
= N x N - 2 x (1 + 3 + 5 + ... + N/2)
= N^2 - 2 x N^2 / 4
= N^2 - N^2 / 2
= N^2 / 2
Therefore, in average, the number of swaps = O(N^2).
Therefore, in the average case time complexity of Bubble sort:
- Number of Comparisons: O(N^2) time
- Number of swaps: O(N^2) time
Space Complexity
The algorithm only requires auxiliary variables for flags, temporary variables and thus the space complexity is O(1).
Comparison with other Sorting Algorithms
The bubble sort algorithm is mainly used to explain theoretical aspects including complexity and algorithm design but rarely used in practice because of how it scales with larger amounts of data. Some complexities of other preferred sorting algorithms are:
| Algorithm | Best Case | Average Case | Worst Case |
|---|---|---|---|
| Bubble Sort | Ω(n) | Ω(n^2) | Ω(n^2) |
| Selection Sort | Ω(n^2) | θ(n^2) | O(n^2) |
| Insertion Sort | Ω(n) | θ(n^2) | O(n^2) |
| Heap Sort | Ω(n log(n)) | θ(n log(n)) | O(n log(n)) |
| Quick Sort | Ω(n log(n)) | θ(n log(n)) | O(n^2) |
| Merge Sort | Ω(n log(n)) | θ(n log(n)) | O(n log(n)) |
| Bucket Sort | Ω(n+k) | θ(n+k) | O(n^2) |
Note: Bubble Sort and Insertion Sort is efficient for the best case that is when the array is already sorted.
With this article at OpenGenus, you must have the complete idea of Time and Space Complexity of Bubble Sort.
