Time and Space Complexity of Circular Linked List

In this article, we have explored Time and Space Complexity of Circular Linked List. We have covered different cases like Worst Case, Average Case and Best Case.

List of Contents

1. Introduction
2. Traversal
3. Insertion
4. Deletion

Pre-requisites:

• Time Complexity Analysis
• Circular Linked List
• Time Complexity Analysis of Linked List
• Basics of Time Complexity Analysis

Introduction

A circular linked list is a linked list where the last node points to the first node instead of NULL. This linked list comes with a pointer END which points to the last element. Since the last element points to the first element, this enables quick traversal from the last element to the first. The circular linked list also enables traversal of the entire linked list starting from any one point.

The circular linked list can be represented as follows:

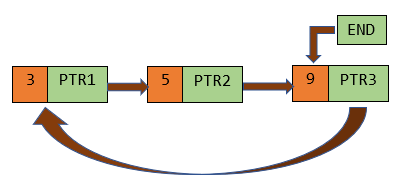
We shall now analyze the time and space complexity of the various operations that can be performed on a circular linked list, such as traversal, insertion, and deletion.

Traversal

In case one wants to traverse the entire linked list, or search for a particular element, one shall first start with the element that *END* is pointing to, and then go through each element of the linked list. Note that one can start from any one element of the linked list.

If there are n elements in the circular linked list, this operation shall run at most n times, until it reaches the element from which it started. Hence, the time complexity of traversal is given by O(n). As there is no extra space used, the space complexity is given by O(1).

Insertion

Best Case

We observe the best case of insertion in a circular linked list when the element is to be inserted at the beginning or at the end.

To insert an element at the beginning, one shall need to make the last element point to the new element, and to make the new element point to the previously first element. Since both these operations take constant time, the time complexity of this operation is given by O(1). Since the space required is also constant, the space complexity is given by O(1).

In order to insert an element at the end, one needs to make the last element as well as the END pointer to point to the new node, and the new node to point to the first element. This is similar to insertion at the beginning, and hence both the time and space complexity of this operation is given by O(1). Note that in a normal linked list, this operation would have a time complexity of O(n), since one needs to traverse to the end of the linked list first. Hence this is an advantage that the Circular Linked List provides over the normal linked list.

Average Case

The average case can be observed when insertion is at any position other than the beginning or at the end. If one needs to insert a node at a given position(not the beginning or the end of the linked list), then one shall first need to traverse to this position. Then, one needs to make the previous element point to this new element, and the new element to point to the next element of the linked list. Note that traversal in a linked list is of O(n) (since one needs to go through the elements one by one until the required position is reached), and that the insertion after reaching the required position is of constant time complexity. Hence, the time complexity of this operation is given by O(n). Since this operation takes up constant space, the space complexity of this operation is given by O(1).

Worst Case

The worst case time complexity also happens to be O(n), which would arise when the element needs to be inserted at the (n-1)^th position.

Deletion

Best Case

The best case is observed when the deletion is at the beginning. For this operation, we only need to make the last element of the linked list point to the element that the first element of the linked list is pointing to. Since this operation takes constant time, and does not need any extra space, both the time and the space complexity of this operation is given by O(1).

Average Case

This situation arises when any other element needs to be deleted. In order to delete an element from the any other position (including the last position), one needs to traverse the linked list until they reach the node before the node that is to be deleted(let this node be TEMP), and ,make this point to the node which succeeds the node to be deleted. In case the node which is deleted is the last node, one needs to ensure that END now points to TEMP.

Here, since traversal takes O(n) time, and since the deletion takes constant time, the time complexity of this operation is given by O(n). As the space used here is constant, the space complexity of this operation is O(1).

Worst Case

As is the case with insertion, the worst case time complexity is also given by O(n), when the last element needs to be deleted.

Conclusion

Here, we conclude the following:

• For traversal, the time complexity is given by O(n), while the space complexity is given by O(1).
• For insertion, the space complexity is given by O(1). The best case time complexity is O(1), when insertion is either at the beginning or at the end, and the average time complexity is O(n), when it is any other position.
• For deletion, the space complexity is given by O(1). The best time complexity here is O(1), when the element to be deleted is the first node, and it is O(n) for all other cases.

The time complexities can be summarized as follows:

Operation	Beginning	End	Other Positions
Insertion	O(1)	O(1)	O(n)
Deletion	O(1)	O(n)	O(n)

With this article at OpenGenus, you must have the complete idea of Time and Space Complexity of Circular Linked List.