
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we are going to explore and calculate about the time and space complexity of binary search tree operations. But before moving to this part we must need to have a clear knowledge of binary search tree and the operations that can be performed.
Table of contents:
- Introduction to Binary Search Tree
- Searching operation
- Time and Space Complexity analysis
- Insertion operation
- Time and Space Complexity analysis
- Deletion operation
- Time and Space Complexity analysis
- Complexities of all operations
Pre-requisites:
The summary is as follows:
| Operation | Worst Case | Average Case | Best Case | Space |
|---|---|---|---|---|
| Search | O(N) | O(logN) | O(1) | O(N) |
| Insert | O(N) | O(logN) | O(1) | O(N) |
| Delete | O(N) | O(logN) | O(N) | O(N) |
Introduction to Binary Search Tree
Binary Search Tree is a node-based binary tree data structure which has the following properties:
- The right subtree of a node contains nodes with values or keys greater than the node's value or key.
- The left subtree of a node contains nodes with values or keys smaller than the node's value or key.
- The left and right subtree each must also be a binary search tree(which means the left and right subtree must satisfy all the above mentioned properties).
See the below attached image for better understanding.
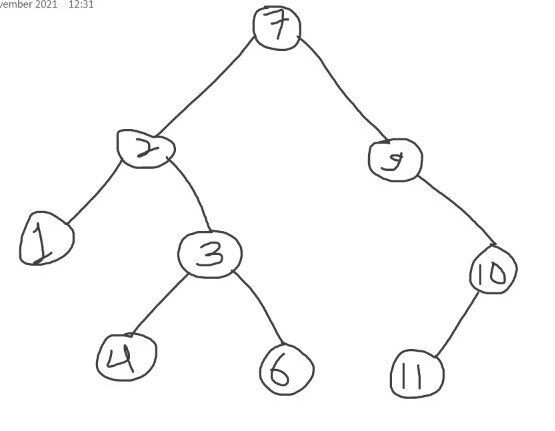
In this image we can see that root node's (topmost node) value is greater than all the nodes present in it's left side or in left subtree. All the nodes in the right subtree of root node have keys greater than the root node's key. All the nodes in left and right subtree are also satisfying the above mentioned properties of binary search tree.
Now after exploring the properties of a binary search tree we will understand some operations which are possible in it. The main operations in binary tree are: search, insert and delete. We will discuss about these operations one by one in detail.
Searching operation
The search operation in a binary search tree is similar to the binary search algorithm. In binary search we will be given a sorted array and we have to search for an element so we start with finding the middle element in the array and compare it with the element to be searched. If the element to be searched is equal to the middle element then we will stop and simply return that element. But if the element to be searched is smaller than the middle element we will discard the right subarray as the elements are in sorted form so we can easily say that the element will be present in left subarray and if the element is found to be greater than the middle element we will search in right subarray discarding the left subarray. So in this way we will keep on reducing the array size into half till we get our target element(element to be searched) or we are left with only one element.
Same procedure is applicable in the case of binary search tree. In this we will be given a tree and a target value that needs to be searched. We will start comparing that element with the root node's value. If the element to be searched is equal to the root node's value we will simply stop and return that element as it is successfully searched. But if the element is smaller than the root node's value we will discard the right subtree of root node as after learning the properties of binary search tree we can say that the element needs to be searched in left subtree as all the node values in left subtree will be smaller than the root node value. If the element is greater than the root node's value we will discard the left subtree of root node because all the nodes in right subtree have values greater than the root node value so we will search for the element in the right subtree. By this way we will keep on reducing the size of binary search tree till we find the element that needs to be searched or we are left with one node only. We can see that the procedure is same as what we have done in binary search algorithm and this is the reason for the name Binary Search Tree.
Let us see a pseudocode of what we have discussed above.
Search(root, key)
while root != NULL and key != root.key then
if key < root.key then
root = root.left
else
root = root.right
end if
repeat
return x
Time and Space Complexity analysis:
-
Time complexity:
i. Best case: When we get the root node as the node which is supposed to be searched then in that case we have to make onle one comparison so time taken would be constant. Time complexity in best case would be O(1).
ii. Average case: When there is a balanced binary search tree(a binary search tree is called balanced if height difference of nodes on left and right subtree is not more than one), so height becomes logN where N is number of nodes in a tree.
In search operation we will keep on traversing through nodes one by one, suppose if we find the element in second level so for doing so we have done 2 comparisons, if we get element in third level we will be doing 3 comparisons so in this way we can say that the time taken to search for a key in binary search tree is same as the height of the tree which is logN, so time complexity for searching is O(logN) in average case.
Note: Average Height of a Binary Search Tree is 4.31107 ln(N) - 1.9531 lnln(N) + O(1) that is O(logN).
iii. Worst case: If the tree is unbalanced or if it is skewed binary search tree(skewed binary search tree is a tree in which there are no nodes available in left subtree or right subtree see the image below to get better understanding)
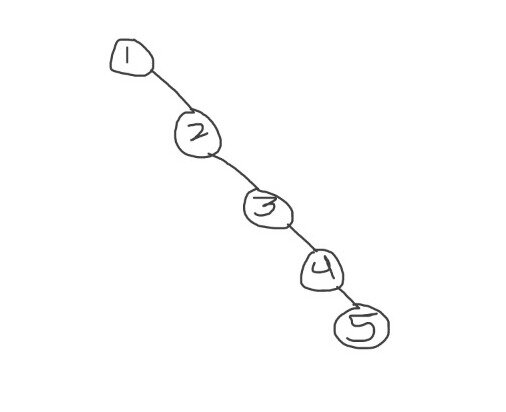
In this case we have to traverse from root to the deepest leaf node and in that case height of the tree becomes n and as we have seen above time taken is same as the height of the tree so time complexity in worst case becomes O(n).
- Space complexity: The space complexity of searching a node in a BST would be O(n) with 'n' being the depth of the tree(number of nodes present in a tree) since at any point of time maximum number of stack frames that could be present in memory is 'n'.
Insertion operation
In binary search insertion is performed in the leaf node. So first we will perform searching operation in it in the same way what we have done above. If the element to be inserted is not present in the tree we insert that element but we have to check whether that element is greater or smaller as compared to the leaf node , if it is smaller insert it to the left side of leaf node and if it is greater insert it to right side of the leaf node. So basically for insertion we are performing two operations first is searching and second is insertion.
In the below attached image I have shown how to insert a node in a binary search tree. We are given a tree and we have to insert 5 in it , so go to the last leaf node on left subtree as root node 7>5 and then at 4 simply insert 5 to the right of 4 as 5>4.

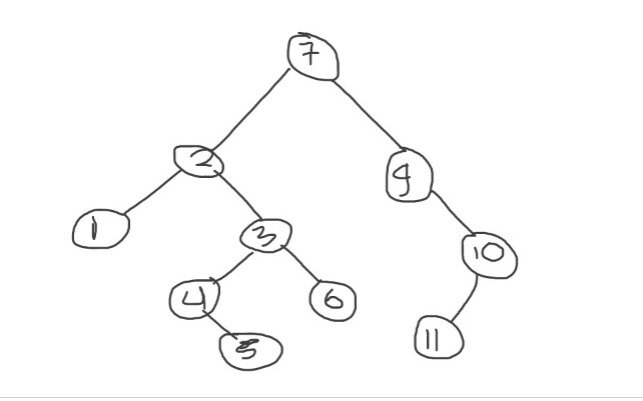
Let us see a pseudocode of what we have discussed above.
Insert(c, z)
a := NULL
b := c.root
while x != NULL do
a := b
if z.key < b.key then
b := b.left
else
b := b.right
end if
repeat
z.parent := a
if a = NULL then
c.root := z
else if z.key < a.key then
a.left := z
else
a.right := z
end if
The procedure maintains a tail pointer a as a parent of b. After initialization on the while loop causes the pointers to be updated. If a is null, the BST is empty, thus z is inserted as the root node of the binary search tree c, if it isn't null, we compare the keys and insert the node accordingly.
Time and Space Complexity analysis:
-
Time complexity:
i. Best case: When we want to insert the root node as the node which is supposed to be inserted then in that case the tree must be empty and we simply insert it in constant time. Time complexity in best case would be O(1).ii. Average case: Just like searching the time complexity for inserting a node is also depends on the height of the tree which is logN. As in this first we are searching for the element whether it is present or not and then we inserting that element in the leaf node. So it totally depends on the height of the tree as first we are making comparisons or searching(this step takes O(log N) time) and then simply inserting the element(this step takes constant time). So overall time complexity will be O(log N) but we will achieve this time complexity only when we have a balanced binary search tree.
So time complexity in average case would be O(log N), where N is number of nodes.
Note: Average Height of a Binary Search Tree is 4.31107 ln(N) - 1.9531 lnln(N) + O(1) that is O(logN).
iii. Worst case: If there is a skewed or an unbalanced binary search tree we have to travel from root to last or deepest leaf node and height of the tree becomes n. So time complexity will be O(n) as searching each node one by one till last leaf node takes O(n) time and then we will insert the element which takes constant time. So time complexity is O(n) where n is the number of nodes.

- Space complexity: The space complexity of inserting a node in a BST would be O(n) with 'n' being the depth of the tree since at any point of time maximum number of stack frames that could be present in memory is 'n'.
Deletion operation:
Deletion operation in a binary search tree consists of three cases. They are:
-
When we are supposed to delete a leaf node and in this case we simply delete the leaf node by traversing to that node and delete it.
-
When we are supposed to delete a node having only one child and in this case first we traverse to that node and then copy the the child of that node(that is to be deleted) in the place of its parent and delete that parent node and its child will occupy its parent place.
-
When we are supposed to delete a node having two children and in this we have to find inorder successor or inorder predecessor depending upon the given tree. Now two new terms are introduced. Inorder successor is a node with minimum value in right subtree of the root node. Inorder predecessor is a node with maximum value in left subtree of the root node. So after finding this(inorder successor or predecessor) we need to copy the contents of inorder successor or predecessor and delete that node which is to be deleted having two children. When right child is not empty we find inorder successor and if left child is not empty we will find inorder predecessor.
In the below attached image you can see that there is no inorder predecessor available but inorder successor is there so we find that.
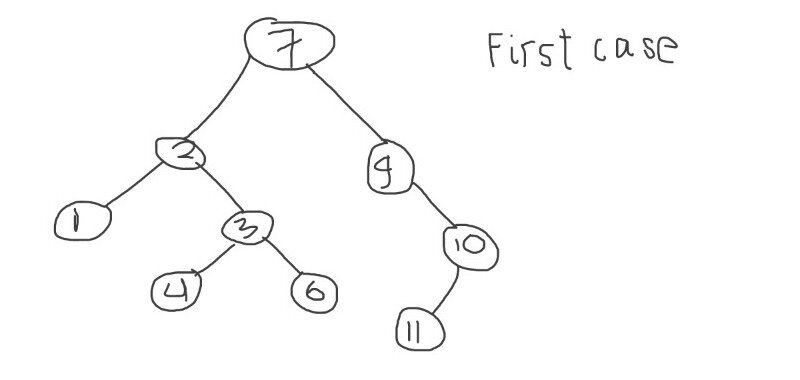
I am attaching an image which describes all the above mentioned cases with a tree diagram. It will help you all in visualizing the exact delete operation in a binary search tree.
Below is the original tree:

first case: when leaf node is to be deleted as we have simply deleted leaf node 5.
second case: when node to be deleted has one child, we will delete 10 and replace it with it's child node 11.
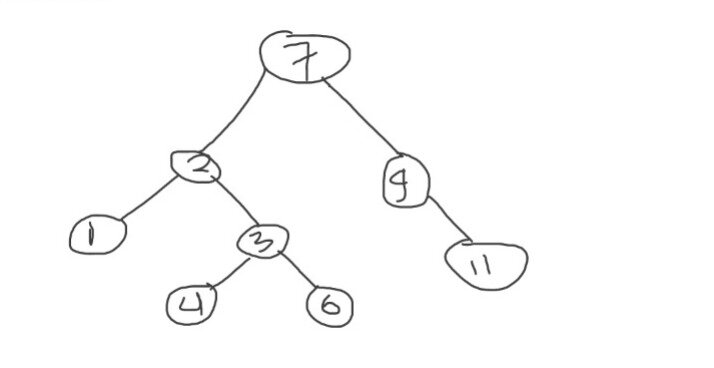
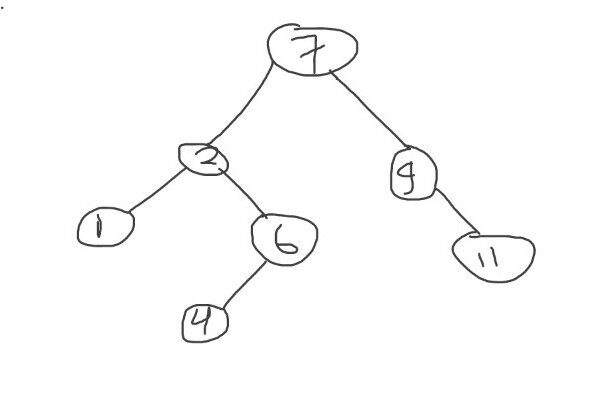
third case: when node to be deleted has two children, after finding inorder precedessor then replace it in the place where node is deleted, so delete 3 and place 6(inorder predecessor) at this place.
Let us a pseudocode for this:
Delete(c, z)
if z.left = NULL then
Shift(c, z, z.right)
else if z.right = NULL then
Shift(c, z, z.left)
else
x := Successor(z)
if x.parent != z then
Shift(c, x, x.right)
x.right := z.right
x.right.parent := y
end if
Shift(c, z, x)
x.left := z.left
x.left.parent := x
end if
Shift(c, a, b)
if a.parent = NULL then
c.root := b
else if a = a.parent.left then
a.parent.left := b
else
a.parent.right := b
end if
if b != NULL then
b.parent := a.parent
end if
The Delete function has 3 special cases mentioned above. The Shift function is used within the deletion algorithm for the purpose of replacing the node a with b in the binary search tree.
Time and Space Complexity analysis
- Time complexity:
i. Best case: When the tree is balanced we have to traverse through a node after making h comparisons for searching a node which takes time which is directly proportional to the height of the tree (logN) and then copying the contents and deleting it requires constant time so the overall time complexity is O(log N) which is the best case time complexity.
ii. Average case: Average case time complexity is same as best case so the time complexity in deleting an element in binary search tree is O(log N).
Note: Average Height of a Binary Search Tree is 4.31107 ln(N) - 1.9531 lnln(N) + O(1) that is O(logN).
iii. Worst case: When we are given a left skewed or a right skewed tree( a tree with either no right subtree or no left subtree), then we have to traverse from root to last leaf node and the perform deletion process so it takes O(n) time as height of the tree becomes 'n' in this case. So overall time complexity in worst case is O(n).

- Space complexity: The space complexity of this algorithm would be O(n) with 'n' being the depth of the tree since at any point of time maximum number of stack frames that could be present in memory is 'n'.
Complexities of all operations
The summary is as follows:
| Operation | Worst Case | Average Case | Best Case | Space |
|---|---|---|---|---|
| Search | O(N) | O(logN) | O(1) | O(N) |
| Insert | O(N) | O(logN) | O(1) | O(N) |
| Delete | O(N) | O(logN) | O(N) | O(N) |
So now I would like to conclude this topic as we have discussed about various possible operations in a BST(binary search tree) and I want all of you who are reading this article at OpenGenus must learn how these operations are applied in a BST and also try to implement based on the approach we have discussed. Happy coding.
Thank you.
