In this article, we will be discussing about the idea of Asymptotic Analysis of Algorithms, 3 asymptotic notations used to represent the time complexity of an algorithm along with examples and much more.

Contents

1. Introduction
2. Notion of Efficiency
3. Asymptotic Notations
4. Big Oh
5. Big Omega
6. Big Theta
7. Asymptotic Observations
8. Asymptotic analysis by taking limits
9. Examples with growth rate
10. Examples of asymptotic formulas
11. Example with an Algorithm
12. Analysing Algorithms
13. Which should be choosen?

Introduction

We all need to make efficient programs to save space (memory) and time.
Among space and time, developers usually focus more on Time complexity. If we have two algorithms to do an operation and we need to find the best one among these two then, we have to use asymptotic notation.

Asymptotic Analysis is an analysis technique for Algorithms that estimates the Time Complexity as the input size tends to increase infinitely. It gives a good idea of the strength of an Algorithm theoretically.

Notion of Efficiency

Computer A execute 10 billion instruction per sec & B execute 10 million per sec.So A is 1000 times faster than B.Let us assume that each of them sort 10 million numbers.Let machine A do selection sort .The time taken is $2*(10^7)^2$ instruction/($10^10$) instruction per sec $= 20000$ sec= more than 5.5 hours.
Let machine B do Merge sort .The time taken is $50*(10^7)*log(10^7)$ instruction/($10^7$) instruction per sec $=1163$ sec=less than 20 minutes.

Even though Machine A was faster we saw that Machine B did well.This proves that merge sort is much better than selection sort.

But if this calculations changes with machine to machine it is not reliable.so we introduce the concept of Asymptotic notations.

Asymptotic Notations

There are 3 main standard Notations for Asymptotic Analysis:

1. Big Oh
2. Big Omega
3. Big Theta

Big Oh (O)

It is denoted by O. A function $f(n)$ is said to be $O(g(n))$ if and only if there exists a constant c and a constant $n_0$ such that $0\ <=\ f(n)\ <=\ cg(n)$ for all $n\ >=\ n_0$.$$g(n)\ can\ be\ N,\ log(N),\ N^2\ and\ other\ functions$$.It defines the upper bound for the function.The function cannot go beyond g(n) after N=N₀.

We will see an example:

Let us take $f(n)$ to be $N^2+1$. Let $g(n)=n^3$
So for $f(n)$ to be $O(g(n))$ it must satisfy: $0\ <=\ N^2\ +\ 1\ <=\ c.N^3$
We must find a value of c for which this is true.
Let n=2.Then $n^2+1$=4+1=5
$n^3$=8
for n=3
$n^2+1=9+1=10$
$n^3$=27

So we can see that for all n>n0 $n^2$+1 < $n^3$.Therefore here c=1 and $n_0$=2.herefore f(n)=O($n^3$).Now lets check whether it is O($n^2$)
0<=$n^2$+1<=c.$n^2$

Let n=2 Then $n^2+1=4+1=5$
$n^2$=4
If we put c=2
Then $c.n^2=8$

Now if we put any value n>2 we get $c.n^2 > n^2+1$.Therefore $f(n)$=$O(n^2)$ for c=2 and for all $n_0$>=2.Here we can see $f(n)$=$O(n^2)$=$O(n^3)$.We can say that if f(n) is $O(n^2)$ then it will be $O(n^3)$,$O(n^4)$, etc...$n^2$ is the tighter bound while others are looser bound.The best answer is minimum $g(n)$ which is $n^2$.

Therefore $f(n)$=$O(n^2)$ for c=2 and for all $n_0$>=2

We only care about the area after $n_0$ not before it.This can be represented graphically as:

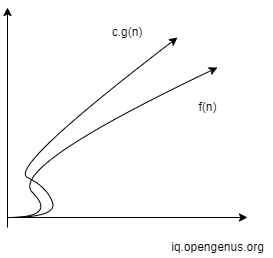
Big Omega (Ω)

Big Omega is denoted by Ω. A function $f(n)$ is said to be $O(g(n))$ if and only if there exists a constant c and a constant $n_0$ such that $0\ <=\ cg(n)\ <=\ f(n)$ for all $n\ >=\ n_0$.

$g(n)$ can be N, log(N), $N^2$ and other functions. It defines the lower bound for the function.The function cannot go below $g(n)$ after $n=n_0$.

We will see an example:

Lets take $f(n)$ to be $n^3+1$.Let $g(n)=1$ .So for $f(n)$ to be $O(g(n))$ it must satisfy:$0<= c <= n^3+1$.We must find a value of c for which this is true.

Let c=1 Then $0<= 1 <= n^3+1$
let $n_0$=1 Then $0<= 1 <= 2$
So we can see that for all n>$n_0$ $1 < n^3+1$.Therefore here c=1 and $n_0$=1.Therefore $f(n)=Ω(n^3)$

Now lets check whether it is $O(n^3)$ . $0\ <=\ c.n^3\ <=\ n^3+1$
Let n=2 Then $n^3+1=8+1=9$
$n^3=8$
If we put c=2 Then $c.n^3=16$

Now if we put any value n>2 we get $c.n^3<=n^3+1$.Therefore $f(n)=Ω(n^3)$ for c=2 and for all $n_0>=2$.Here we can see $f(n)=Ω(1)=Ω(n^3)$.

We can say that if $f(n)$ is $Ω(n^3)$ then it will be $Ω(n^2)$,$Ω(n)$, etc...The best answer is maximum $g(n)$ which is $n^3$.Therefore $f(n)=Ω(n^3)$ for c=2 and for all $n_0>=2$

We only care about the area after $n_0$ not before it.This can be represented graphically as:

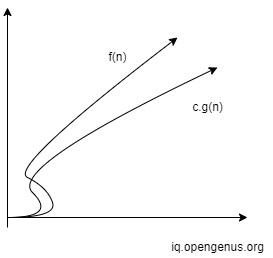
Big Theta (Θ)

Simply we can say that for a function $g(n)$ if $f(n)$ is $O(g(n))$ and $(g(n))$ then it is called $Θ(g(n))$. It tightly bounds the functions. It provides both the upper bound and lower bound. It is denoted by Θ. A function $f(n)$ is said to be $O(g(n))$ if and only if there exists a constant c1, c2 and a constant $n_0$ such that $0\ <=\ c_2g(n)\ <=\ f(n)$ and $0\ <=\ f(n)\ <=\ c_1g(n)$ for all $n>=n_0$.That is : $c_2g(n)\ <=\ f(n)\ <=\ c_1g(n)$.

$g(n)$ can be N, log(N), $N^2$ and other functions. It gives the best picture of run time of an algorithm.If a function is big theta of a function then it is automatically big oh and big omega of that function.

We will see an example:

Lets take $f(n)$ to be $n^3+1$ Let $g(n)=n^3$
So for $f(n)$ to be $O(g(n))$ it must satisfy: $0\ <=\ n^3+1\ <=\ c.n^3$. We must find a value of c for which this is true.

Let $n_0=2$. $n^3+1=9$
$n^3+=8$
Let c=2 Then $0\ <=\ 16\ <=\ 9$

So, we can see that for all $n>n_0$, $n^3+1$ < $2.n^3$ Therefore here c=2 and $n_0=2$.Therefore $f(n)=O(n^3)$.

Now lets check whether it is $Ω(n^3)$. Let $g(n)=n^3$. For it to be $Ω(g(n))$, it must satisfy: $0\ <=\ c.n^3\ <=\ n^3+1$

Let n=1 Then $n^3+1=1+1=2$
$n^3=1$
If we put c=1 Then $c.n^3=1$
Now if we put any value $n>1$ we get $c.n^3<=n^3+1$.Therefore $f(n)=Ω(n^3)$ for c=1 and for all $n_0>=1$.Here we can see $f(n)=Ω(n^3)=O(n^3)$.That is: $f(n)=Θ(n^3)$. $n^3$ tightly bounds the function $f(n)=n^3+1$.

This can be represented graphically as:

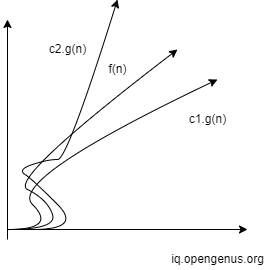
We will find Θ in most the cases.

Asymptotic Observations

We can see the following properties for Big Oh,Omega and theta:

1. Reflexive

Big O,Big Omega and Big theta are reflexive.

As for $n^2$, $O(n^2)$ is $n^2$. So here $n^2$ is mapped to itself. Therefore it is reflexive.

Similarly, for big omega $n^2$, $Ω(n^2)$ is $n^2$So here $n^2$ is mapped to itself. Therefore it is reflexive. For big theta: For a function $n^2$ $Θ(n^2)$ is $n^2$.So here $n^2$ is mapped to itself .Therefore it is reflexive

2. Symmetric

Big Oh,Big Omega and Big theta are not symmetric.The proof is pretty simple.
Let the function be n. n can be $O(n^2)$ but $n^2$ cannot be $O(n)$. So, it is not symmetric.Similarly for Big theta and Big Omega.

3. Transitive

Big Oh,Big Omega and Big theta are Transitive.
Let us see it for Big Oh.for $n=O(n^2)$ and $n^2=O(n^3)$.Therefore, $n=O(n^3)$
Similarly for Big Omega and Theta.

Asymptotic analysis by taking limits

If we have 2 functions f(n) and g(n).Let us consider taking their limits
$\lim\limits_{n \to ∞}\frac{f(n)}{g(n)}$ .There are 3 cases for the limit value

1. =0 -- $O(g(n))$
2. a constant --It is $Θ(g(n))$
3. infinity --$Ω(g(n))$

compute $\lim\limits_{n \to ∞}\frac{f(n)}{g(n)}$

If the result is some finite,positive constant c,then the rates of growth of both $f(n)$ and $g(n)$ are same.That is one is big theta of the other.
Example:
$\lim\limits_{n \to ∞}\frac{an^2+b.n+c}{n^2}$= a which is a finite positive constant,therefore $an^2+b.n+c = Θ(n^2)$

if $\lim\limits_{n \to ∞}\frac{f(n)}{g(n)}$ turn out to be 0,then it means $f(n)$ has smaller rate of growth than $g(n)$.That is $g(n)$ is big Oh of the other function $f(n)$.
Example:
$\lim\limits_{n \to ∞}\frac{an^2+b.n+c}{n^3}$ = 0
therefore $an^2+b.n+c = O(n^3)$.

if $\lim\limits_{n \to ∞}\frac{f(n)}{g(n)}$ turn out to be infinity,then it means $g(n)$ has smaller rate of growth than $f(n)$.That is $g(n)$ is big Omega of the other function $f(n)$.
$\lim\limits_{n \to ∞}\frac{an^2+b.n+c}{n}$ = ∞
therefore $an^2+b.n+c = Ω(n)$

Let us see some more examples:
1.$\lim\limits_{n \to ∞}\frac{an+b.n+c}{n^3}$ = 0
therefore $an+b.n+c = O(n^3)$.

2.$\lim\limits_{n \to ∞}\frac{an^4+b.n+c}{n}$ = ∞
therefore $an^4+b.n+c = Ω(n)$

3.$\lim\limits_{n \to ∞}\frac{n^6}{n^6}$ = 1 which is a finite positive constant,therefore n^6 = Θ(n^6)

4.$\lim\limits_{n \to ∞}\frac{an}{n^5}$ = 0
therefore an = O(n^5).

5.$\lim\limits_{n \to ∞}\frac{bn^2+c}{n}$ = ∞
therefore b.n^2+c = Ω(n)

Examples with growth rate

Consider the function $f(n)=3n^2+2n+3$

Now if we consider growth rate of $f(n)$ for different values of n then:

n	$3n^2$	2n	3
10	300	20	3
100	30000	200	3
1000	3000000	2000	3

Here we can see that the term $3n^2$ has the maximum growth rate.So we can limit the function to $f(n)= 3n^2$ .As 3 is a constant if we remove it we get $f(n)= n^2$.So we can say that $f(n)$ is similar to $n^2$.Therefore $f(n)= Θ(n^2)$.

$f(n)=n+log(n)$

if we consider growth rate of $f(n)$ for different values of n then:

n	n	$log(n)$
2	2	1
$2^10$	$2^10$	10
$2^1000$	$2^1000$	1000

Here we can see that the term n has the maximum growth rate.So we can limit the function to $f(n)= n$ .So we can say that $f(n)$ is similar to n.Therefore $f(n)= Θ(n)$.

Examples of asymptotic formulas

Below are some functions and it's asymptotic expansion

Function	Asymptotic expansion
$n!$	$√2πn(n/e)^n$
Partition function $p(n)$	$\frac{1}{4n√3}*(e^(π√2n/3))$
Airy Function $Ai(x)$	$ \frac{(e^-2/3(x^3/2))}{2√π(x^1/4)}$

Example with an Algorithm

Let us consider the program for factorial of a number

int factorial(int n)
{
    if (n == 0)
        return 1;
    else
        return n * factorial(n - 1);
}

Here if n==0 then 2 operations take place

1. Comparison(n==0)
2. return statement

if n>0 then 3 operations take place

1. Comparison(n==0) comes to else part
2. multiplication
3. return

for n let the time taken be T(n)

We can see from the program that T(n)=3+T(n-1)
In next step it becomes T(n)=3+3+T(n-2)

T(n)=3+3+3+T(n-3)
.
.
.
T(n)=3n+T(0)
T(n)=3n+2

We can see that here the dominating term is n
Therefore T(n)=Θ(n)

Analysing Algorithms

Let us see the recursive formula for linear search:

T(n)= 1,if n==1;
      1+T(n-1) if n>1

Which means that the time required is 1 if only one element is remaining(n==1) as we only need to compare that element to the given key.
If n>1 then 1 for comparing the element to the key and T(n-1) for the rest elements in a recursive way.Here the cost at each step is 1 for comparing the element to the key.

If we draw a tree with the cost(that is 1) at each level it will look like this:

1
 1 
  1
   1 
    .
     .
      n times

Thus the total cost is 1+1+1+... n times that is n.
Therefore the time complexity of linear search is Θ(n).

Now lets take the function for binary search.

T(n)= 1,if n==1;
1+T(n/2) if n>1

The time required is 1 if only one element is remaining(n==1) as we dont need to divide it more just compare it with the key.
If n>1 then 1 for comparing the middle element to the key and T(n/2) for the rest half of the elements to the left or right of the middle depending on key value compared to the middle element in a recursive way.Here the cost at each step is 1 for comparing the middle element to the key.
Let us assume that this will go for k steps:

If we draw a tree with the cost(that is 1) at each level it will look like this:

1
 1 
  1
   1 
    .
     .
      k times

Thus the total cost is 1+1+1+... k times that is k

Now for binary search at every level the number n of the elements is divided into 2.It keeps going on until it reaches 1.
That is it stops when $n/2^k=1$
Therefore,$n=2^k$
$k=log(n)$

Therefore, the time complexity of binary search is $Θ(log(n))$.

Which should be choosen?

Among the 3 notations we must choose Θ if a choice is given as it gives both upperbound and lower bound and the function is tigthly contained within it.

With this article at OpenGenus, you must have the complete idea of Asymptotic Analysis.