In this article, we have explained an efficient approach to solve the Skyline Problem using a Divide and Conquer algorithm.

Contents

1. Problem Statement
2. Imp points to find to solve the problem
3. Finding answers to the points
4. Code
5. Input
6. Output
7. Time and Space Complexity

Problem Statement

We are given start point,end point and height of rectangles which forms the buildings.We have to find the skyline formed by these rectangles collectively.

What is a skyline?

A city's skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance

We are provided an array buildings which contain the geometric information of each building
buildings[l] = [leftl, rightl, heightl].

leftl is the x coordinate of the left edge of the lth building.
rightl is the x coordinate of the right edge of the lth building.
heightl is the height of the lth building.

The rectangles are grounded on a flat surface of height 0.

We are tracing the outline by retuning a list of "key points" sorted by their x-coordinate in the form [[x1,y1],[x2,y2],...]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline's termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline's contour.

One thing we have to take care is that here must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...,[2 3],[4 5],[7 5],[11 5],[12 7],...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...,[2 3],[4 5],[12 7],...]

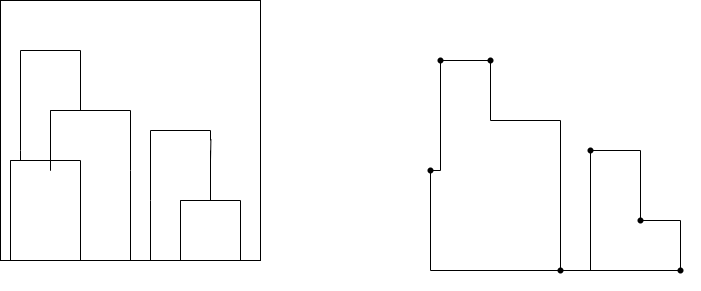
Input: buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,4]]
Output: [[2,10],[3,15],[7,12],[12,0],[15,10],[20,4],[24,0]]

Explanation:
First Figure shows the buildings of the input.
Second Figure shows the skyline formed by those buildings. The black points in second figure represent the key points in the output list.

Imp points to find to solve the problem

1. We have to note the start point of each building
2. We have to note the end point of each building
3. Mechanism to mark consecutive buildings
4. Given x axis value we have to find max y value
5. We have an answer every time the height changes.

Finding answers to the points

For solving 1 and 2 ,to mark start and end ,we are assigning +ve and -ve values to heights.

For example if the building is denoted by (2 9 10) then 2 is start point and 9 is end point.
We denote this by writing 2 ->-10 and 2 ->10 .
Height is made -ve to denote it is starting point and the +ve height denote it is the end point of the building.

So the output of 1 and 2 for this question is:

[2,-10],[9,10],[3,-15],[7,15],[5,-12],[12,12],[15,-10],[20,10],[19,-4],[24,4]

For 3 ,to mark consecutive buildings we will sort the above values in ascending order of x axis:

The result is:
[2,-10],[3,-15],[5,-12],[7,15],[9,10],[12,12],[15,-10],[19,-4],[20,10],[24,4]

Now we can identify the overlapping buildings.

We have to consider the case where 2 buildings start at same point that is have same x coordinate.
For example consider we have both [2,-10] and [2,-15]
When we sort 2 buildings having same x coordinate we have to put the building with more height first as it's endpoint is the point that is present in the skyline.

So after sorting we get

[2,-15] , [2,-10]

For 4,we are maintaining a priority queue such that the top of queue contain the heighest building.

For 5,we have to maintain a variable to store the previous height which is to be compared with the present one to check if there is a change in height.

So summarizing quickly:

• First we will take the given list of buildings and convert them into a pair of values which contains start point and height or endpoint and height.To denote it is start point we will put a negative sign for the height.
• Next we will sort these values in ascending order of x values.When we sort 2 buildings having same x value we have to put the building with more height first.
• Next we will declare a priority queue such that the top of queue contain the heighest building. We have to maintain a variable to store the previous height which is to be compared with the present one to check if there is a change in height.
• So we will store the highest value of y axis (that is present in priority queue currently) in curr.
• If prev not equal to curr then we will add the x axis value and curr to a newly declared list tmp and add it to the result. Then we will make prev as curr.

Code

The code in java for the problem is given below.

public class SkyLine{
	
	public List<List<Integer>> getSkyline(int[][] buildings){

		List<List<Integer>>  result =new ArrayList<>();

		List<int[]> heights=new ArrayList<>();

		for(int[] b :buildings){
			heights:add(new int[]{b[0],-b[2]});
			heights:add(new int[]{b[1],b[2]});
		}

		Collections.sort(heights,(a,b)->{
			if(a[0]!=b[0]) return a[0]-b[0];
			else return a[1]-b[1];
		});

		PriorityQueue<Integer> pq=new PriorityQueue<>((a,b)->b-a);
		pq.offer(0);
		int prev=0;

		for(int[] h :heights){
			if(h[1]<0) pq.offer(-h[1]);
			else pq.remove(h[1]);
			int curr=pq.peek();
			if(prev!=curr){
				List<Integer> tmp= new ArrayList<>();
				tmp.add(h[0]);
				tmp.add(curr);
				result.add(new ArrayList<>(tmp));
				prev=curr;

			}
		}


		return result;
	}
}

I will give you a code walkthrough
First we are declaring the result list for storing the result.Then we are defining list heights which will maintain all the heights of the building.Then we will write a for loop in which we add to the list heights start points,height and endpoints of the building.b[0] denote start point ,b[2] is height of the building.The minus in -b[2] marks that it is the start point.b[1] is endpoint of the building,positive b[2] denote it is end point.
Now to mark consecutive buildings:we are sorting heights based on x axis values.If x values are same then we will sort on basis on value of height.
Next we will declare a priority queue pq.In this priority queue we will keep largest element on top by writing (a,b)->b-a.If nothing is present then it is 0 height.we declare prev as 0.We define a for loop which loop for every h in heights .In that for loop if height is less than 0 it means it is starting point so we will push negative of height to priority queue else h[1]>0 it means we have reached the end of a building so we will remove the building from priority queue.So the top of priority queue will always be the highest value.Next we will store the highest value of y axis (that is present in priority queue currently) in curr.if prev not equal to curr then we will add the x axis value and curr to a newly declared list tmp and add it to the result.Then we will make prev as curr.Thus we have implemented through code the 5 Imp points to find to solve the problem.

Input

It is given in the question the input are:

[[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,4]]

Output

The output of skyline problem for given input will be:

[[2,10],[3,15],[7,12],[12,0],[15,10],[20,4],[24,0]]

Thus we can see that it was easy to solve the problem after we have broken it down to the 5 important points and then write code to solve each point.

Time and Space Complexity

As the code involves a for loop that is for(int[] b :buildings) the time complexity is O(n) where n is the number of elements in buildings.But it also contains Collections.sort whose time complexity is O(nlogn). Therefore the overall time complexity is O(nlogn).

For space complexity we are first declaring a new ArrayList to store our result which will take a space of O(n).We are also defining an extra priority queue ,so the time complexity here is O(n).Therefore the overall time complexity is O(n).

With this article at OpenGenus, you must have the complete idea of Skyline Problem.