In this article, we have explained how to use a Divide and Conquer approach to find the Minimum and Maximum element in array using the theoretically minimum number of comparisons.

Table of contents

1. Problem or Statement
2. Methods to approach the Solution
3. Approach-1: Using Brute force
4. Approach-2: Using Divide and Conquer
5. Conclusion

Let's understand the Problem

Given an array a[] of size 'n', we need to find the minimum and maximum elements in the array using minimum comparisions.

For example:

Let 
Input array elements:

a[] = {10, 8, 9, 20, 5, 15, 3, 12}


Output:

Maximum element in the array is 20
Minimum element in the array is 3

Methods to approach the Solution

1. Brute Force approach using loop.
2. Using Divide and Conquer approach.

Method-1: Brute force

Algorithm

• Begin max-min
• Having array 'a', size of array 'n', and a pointer "minmax" as input parameters.
• Declare the variables max and min and initialize a[0] to both, i.e.,

int max = a[0]
int min = a[0]

• Now we will start a loop and traverse through the array 'a' from 1 to (n-1)th index, and do compare each element with max and min

for i = 1 to (n-1)

• Do the comparisions as(within the for-loop),
  Condition-1 : if(a[i] > max) then max = a[i], mean if value on i-th index is greater than max, then put max = a[i].

    if a[i] > max
        max = a[i]

Condition-2: if(a[i] < min) then min = a[i], mean if value on the i-th index is less than min, then put min = a[i].

    else
        if a[i] < min 
            min = a[i]

• End of for-loop.
• Now we can return both values(max & min) by storing them into minmax[] array.

minmax[0] = max
minmax[1] = min

• End max-min.

Code

#include<bits/stdc++.h>
using namespace std;

/*-----------Min-Max Function-------------*/
void max_min(int a[], int n, int *minmax){
    int max = a[0];
    int min = a[0];
    for(int i = 1; i < n; i++){
        if(a[i] > max)
            max = a[i];
        else
        if(a[i] < min)
            min = a[i];
    }
    minmax[0] = max;    
    minmax[1] = min;
}

/*-------------Driver Function-------------*/
int main(){
    int a[] = {11, 9, 20, 21, 0, 15, 4, 13};    //Taking array 'a'
    int minmax[2] = {0};    //Taking an extra array minmax to store max & min values
    max_min(a, 8, minmax);  //calling function max_min()
    cout<<"\n Maximum element in the array is "<<minmax[0];  //Printing max value
    cout<<"\n Minimum element in the array is "<<minmax[1];  //Printing min value
    return 0;
}

Output:

 Maximum element in the array is 21
 Minimum element in the array is 0

Complexity

Time Complexity: O(n), due to loop
Space complexity: O(1), constant due to array

• Minimum number of comparisions are (n-1) comparisions. For example: Array having elements in Ascending order

a[] = {2, 4, 6, 10, 20, 25}

Output:
Maximum element in the array is 25
Minimum element in the array is 2

Method-2: Divide and Conquer

Algorithm

• In this method, we will use recursive tree method.
• Begin max-min
• Function is having an array 'a', starting index 's', end index 'e', min, max as input parameters.
• Condition-1: If array is having only one element in it. Then max = a[s] and min = a[s] and return the values.

if(s == e)
    max = a[0]
    min = a[0]

• Condition-2: If array is having only two elements in it. Then the bigger element from the two will be assign to max and the smaller one will assign to min, i.e.,

if(s == e-1)
    if(a[s] < a[e])
        max = a[e]
        min = a[s]
    else
        max = a[s]
        min = a[e]

• Condition-3: Take 3 variables lete say mid, max1, min1 and assign them as follows:

mid = (s + e)/2
min1 = INT_MAX
max1 = INT_MIN

mid is to divide the array in first half and second half.
Now we will call the max-min in recusive way and in the process change the values of max and min accordingly.
i.e.,

max_min(a, s, mid, min, max)

Here we are giving the first half of array in recursive tree way.

max_min(a, mid+1, e, min1, max1)

Here we are giving the second half of the array.
Now we will compare the max with max1 and min with min1 and change the max and min if needed,

if(max1 > max)
    max = max1
if(min1 < min)
    min = min1

• End max-min

Code

#include<bits/stdc++.h>
using namespace std;


/*-----------Min-Max Function-------------*/
void max_min(int a[], int s, int e, int *min, int *max){
   //condition-1
   if(s == e){
    *max = a[s];
    *min = a[s];
   }
   //end condition-1
   
   else
   //condition-2
   if(s == e-1){
       if(a[s] < a[e]){
           *max = a[e];
           *min = a[s];
       }
       else{
           *max = a[s];
           *min = a[e];
       }
   }
   //end condition-2
   
   //condition-3
   else{
       //Divide
       int mid, max1, min1;
       max1 = INT_MIN;
       min1 = INT_MAX;
       mid = (s + e)/2;
       max_min(a, s, mid, min, max);
       max_min(a, mid+1, e, &min1, &max1);
       //Conquer
       if(max1 > *max)
            *max = max1;
       if(min1 < *min)
            *min = min1;
   }
   //end condition-3
   
}

/*-------------Driver Function-------------*/
int main(){
    int a[] = {11, 9, 10, 25, 8, 15, 4, 13, 2};    //Taking array 'a'
    int max, min;   //taking max and min elements
    max = min = a[0];
    max_min(a, 0, 8, &min, &max);  //calling function max_min()
    cout<<"\n Maximum element in the array is "<<max;  //Printing max value
    cout<<"\n Minimum element in the array is "<<min;  //Printing min value
    return 0;
}

Output:

 Maximum element in the array is 25
 Minimum element in the array is 2

Complexity

Time Complexity: O(n)
Space Complexity: O(log(n)), due to recursive tree(stack)

• Number of comparisions:
  Condition-1: zero comparision, if n = 1
  Condition-2: one comparision, if n = 2
  Condition-3: 2T(n/2)+2 comparisions, if n > 2
  Total comparisions: (((3n)/2)-2) {If 'n' is power of 2}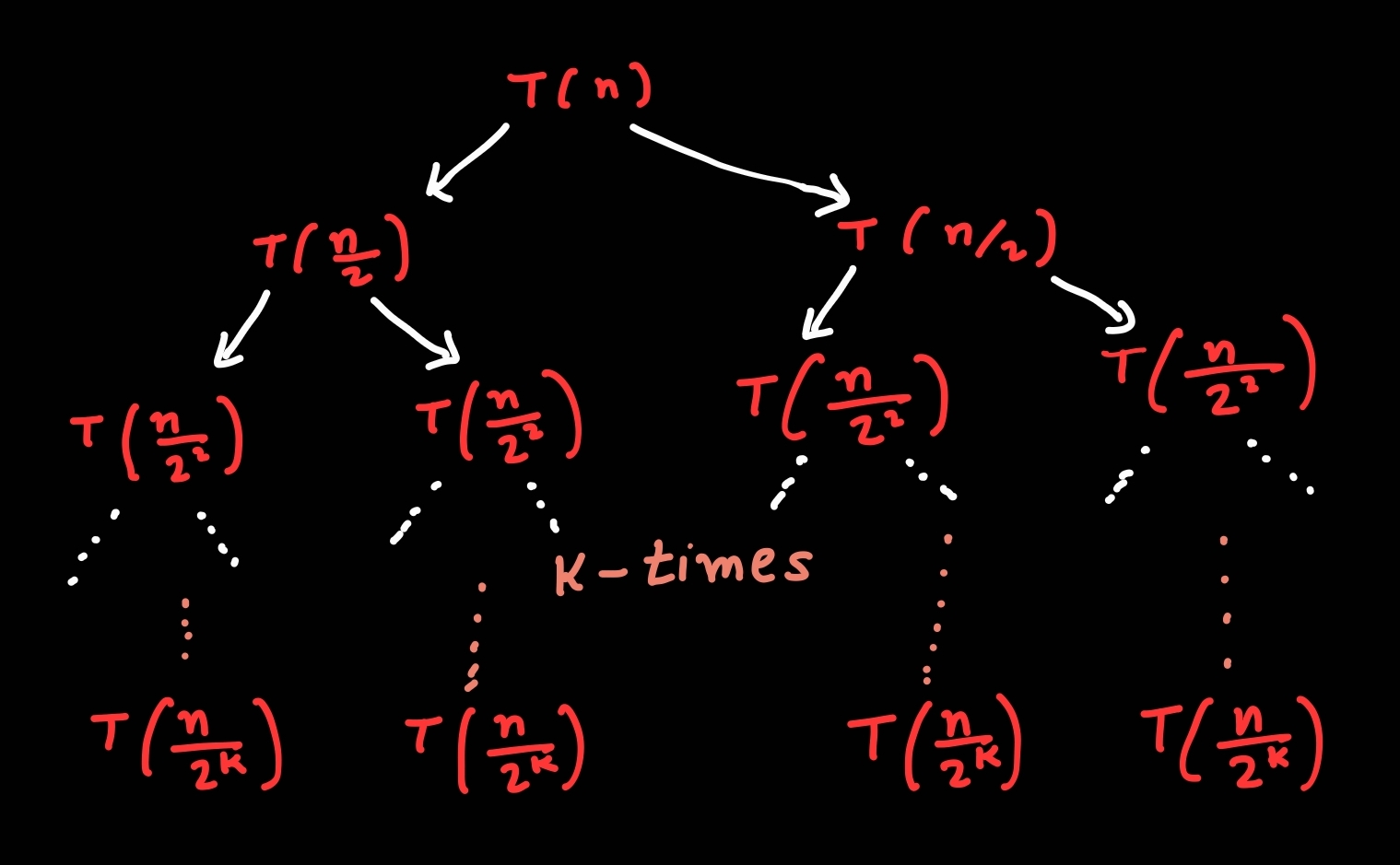

  

  T(n) = 2*T(n/2) + 2
  T(n) = 2*[2*T(n/(2^2)) + 2] + 2
  T(n) = (2^2)*T(n/(2^2)) + (2^2) + 2
  ... k-times
  T(n) = (2^k)*T(n/(2^k)) + (2^k) + ... + (2^2) + 2
  T(n) = (2^k)*T(n/(2^k)) + 2*[(2^k)-1]
  put n/(2^k) = 2
  T(n) = (n/2)*T(2) + 2*[(n/2)-1]
  according to above condition-2, T(2) = 1
  T(n) = (n/2) + 2*[(n/2)-1]
  T(n) = {[(3*n)/2]-2}
  

Conclusion

Brute Force

Time complexity: O(n)
Space complexity: O(1)

Divide and Conquer

Time complexity: O(n)
Space complexity: O(log(n))

• Number of Comparisions in divide and conquer is less than Brute force.
  • Brute force: min -> (n-1) comparisions and
    max -> ((2*n)-2) comparisions.
  • Divide and conquer: (((3*n)/2)-2) comparisions for all cases.

With this article at OpenGenus, you must have the complete idea of finding the Min and Max element in array.