K-th Largest Element in Array

In this article, We will discuss 4 different approaches to find the kth largest element in the given array.

Table of Content:

• Problem Statement
• Approach 1
• Approach 2
• Approach 3
• Approach 4

Problem Statement:

We are given an Array arr and an integer k. We are required to find the kth largest element in the Array.

Example

1. arr = {5, 4, 1, 8, 3, 6, 9}
   k = 5
   Output: 4
   
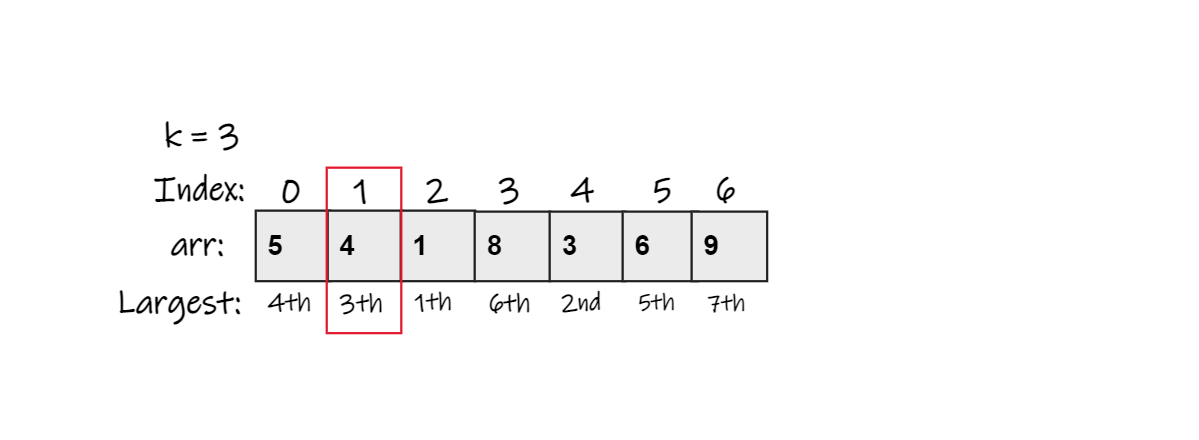
   Explanation: We can see that 9 is the largest element and 8 is the second largest and 6 is the third largest element in the Array.
2. arr = {5, 1, 6, 5, 7, 5}
   k = 3
   Output: 5
   
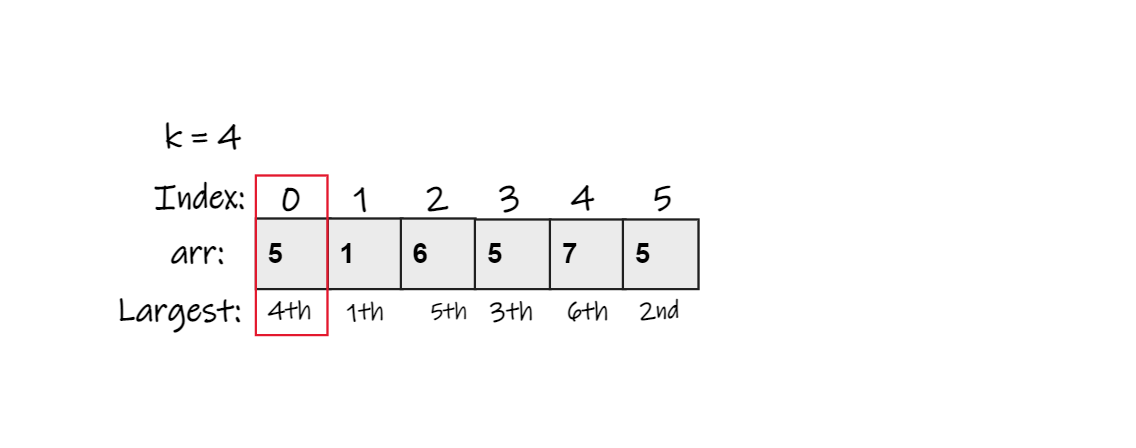
   Explanation: We can see that 7 is the largest and 6 is the second largest and 5 is the third largest but there are 3 five's so 4th largest will be 5.

Approach 1

• In this approach we sort the given array.
• We sort the array in decreasing order. (sort function complexity O(nlogn) )
• The kth element of the array is the answer.
  

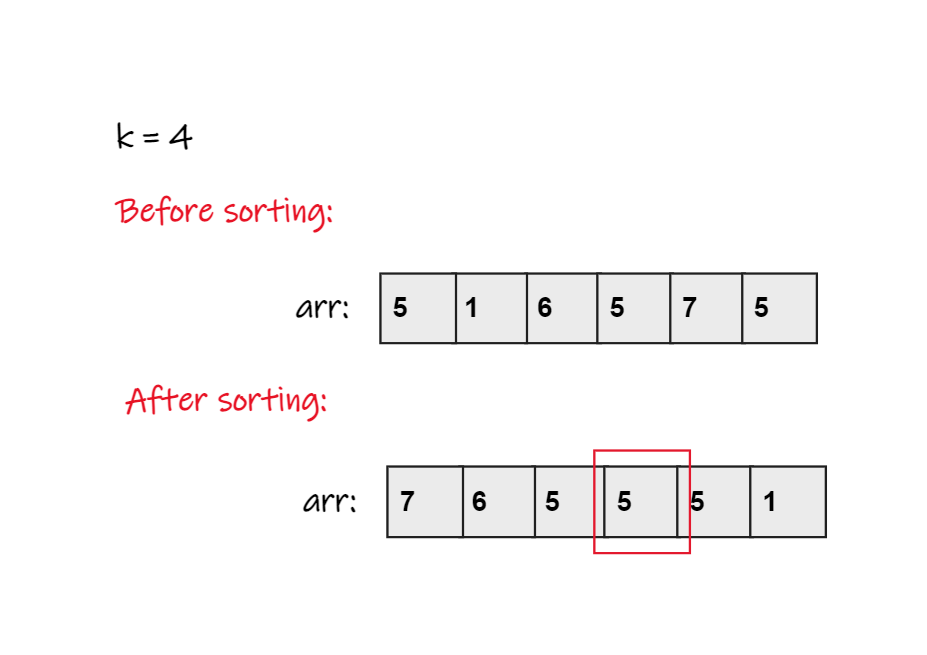
Pseudo Code:

1. Sort the array in Decreasing order.
2. Print kth element.

Complexity Analysis

Time Complexity : O(nlogn) where n is the length of array.
Since we used the sort function whose complexity is n*logn.
Space Complexity: O(1) i.e no extra space required.

Approach 2

• In this approach we sort the array using bubble sort.
• Since we require kth largest element so we will run bubble sort sort which will sort k largest elements in the last of array.
• From the end of array we will print the kth element.

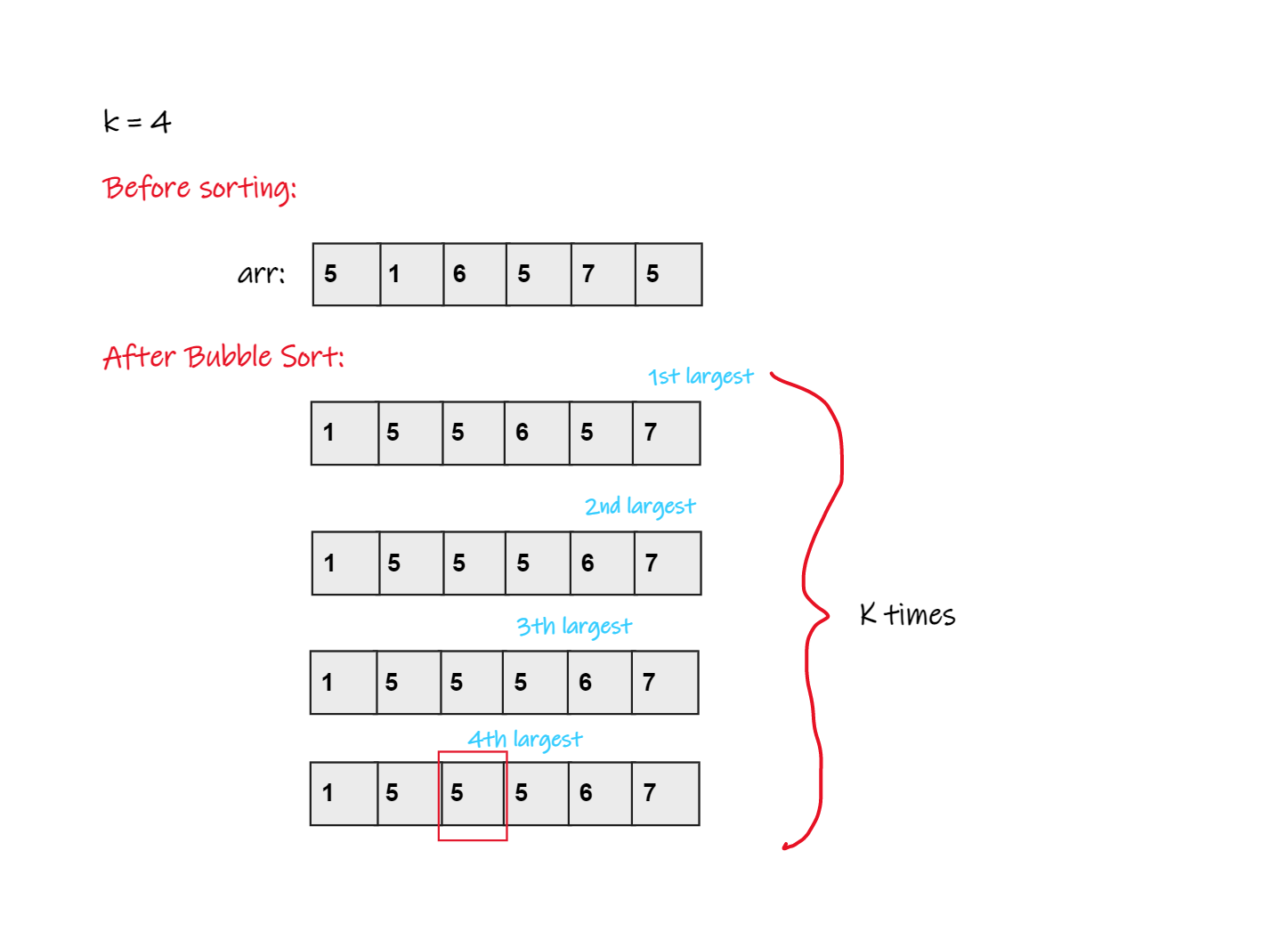
Pseudo Code:

1. Sort k largest elements of the array using bubble sort.
2. Output (n-k) element from the last of array.

Complexity Analysis

Time Complexity : O(klogn)
Generally bubble sort complexity is O(nlogn) but in this approach we have sort k elements only i.e the outermost loop in bubble sort will iterate k time for n elements and that's why the complexity will be k*logn.
Space Complexity: O(1) i.e no extra space is required.

Approach 3

In this approach, we use the Quick Select Algorithm to find the kth largest element in the array.

Pseudo Code:

1. Consider the last element as pivot.
2. Partition the array.
3. If the index of partitioned element is more than (k-1)
   -> Recur the left part of pivot.
4. If the index of partitioned element is less than (k-1)
   -> Recur the right part of pivot.
5. If the pivot index is same as (k-1)
   -> We found the answer.

Code:

#include <bits/stdc++.h>
using namespace std;

int partition(int *arr, int l, int r) {
	int pivot = arr[r], i = l;
	for (int j = l; j <= r - 1; j++) {
		if (arr[j] >= pivot) {
			swap(arr[i], arr[j]);
			i++;
		}
	}
	swap(arr[i], arr[r]);
	return i;
}

int kthlargest(int *arr, int l, int r, int k) {
	
	int index = partition(arr, l, r);
	
	if (index - l == k - 1)
		return arr[index];
	if (index - l > k - 1)
		return kthlargest(arr, l, index - 1, k);
		
	return kthlargest(arr, index + 1, r, k - index + l - 1);

	return INT_MAX;
}

int main() {
	
	int arr[] = {5, 1, 6, 5, 7, 5};
	int n = 6;
	int k = 4;
	
	cout << "Kth largest element is: "<< kthlargest(arr, 0, n - 1, k);
	
	return 0;
}

Complexity Analysis:

Time Complexity : O(n) but in worst-case it's time complexity is O(n^2)
Space Complexity: O(n) due to call-stack.

Approach 4

• In this approach we will use Min-Priority-Queue.
• We initialise a Min-Priority-Queue of size k with the first k elements of the array.We iterate through remaining elements of the array.
• If the current element of array is greater than the top element of Priority Queue then we remove the top element from the queue and insert the element of array in the priority queue.
• After the iteration is complete, the top element of the queue is the answer.

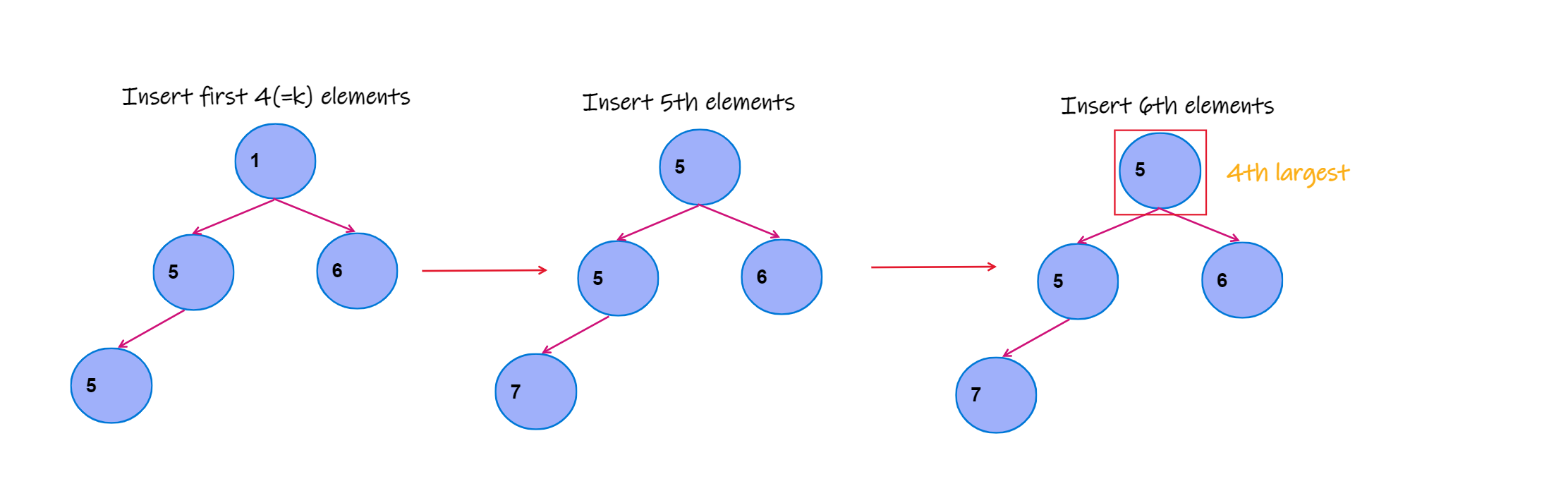
Pseudo Code:

1. Insert first kth element of the array in the min-priority-queue.
2. Iterate over remaining elements of the array.
   2(a). If the element is greater than the top element of queue than we remove the top element from queue and insert the element of array in the queue.
   2(b). Else continue.
3. Top element of the priority queue is the answer.

Code:

    #include<bits/stdc++.h>
    using namespace std;
    
    // function to find kth largest element
    int find(vector<int>& arr, int k) {
    
        // Min-Heap-Priority-Queue
        priority_queue<int, vector<int>, greater<int>> pq;
        
        //Inserting first k elements in the queue
        for(int i=0;i<k;i++) {
            pq.push(arr[i]);
        }
        
        //Inserting k largest elements of array in thr queue
        for(int i=k;i<arr.size();i++) {
            int kMax = pq.top();
            if(kMax < arr[i]) {
                pq.pop();
                pq.push(arr[i]);
            }
        }
        return pq.top();
    }
    
    int main() {
    
        vector<int> arr = { 5, 1, 6, 5, 7, 5};
        int k = 4;
        
        //function call
        int ans = find(arr, k);
        
        cout<<"Kth largest element is: "<<ans<<endl;
        
        return 0;
    }

Output : Kth largest element is: 5

Complexity Analysis:

Time Complexity : (n-k)logk
We iterate over the remaining (n-k) elements and did insertion and deletion in the priority queue according to our neccesity. And the complexity for insertion and deletion in the priority queue is logn.

Space Complexity: O(k) where k is the kth largest element to find.
As we stored k elements in the priority queue.
Thank You!

With this article at OpenGenus, you must have the complete idea to find the K-th largest element in an array.