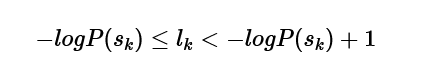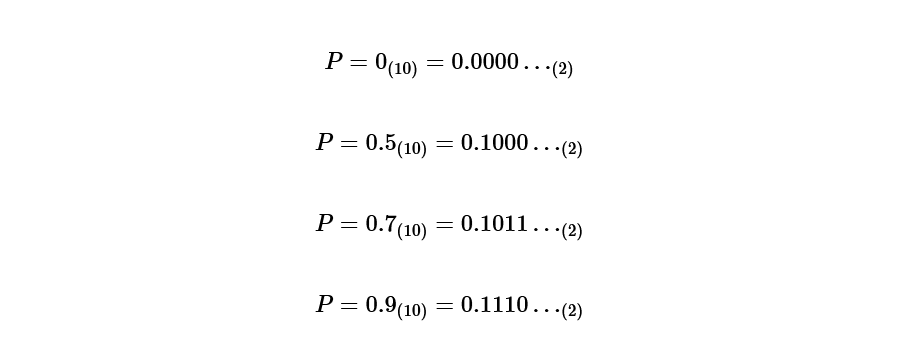Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article we are going to talk about the classic data compression algorithm called "Shannon-Fano code."
Table of contents:
- What is a Shannon-Fano code?
- How Shannon-Fano encoding works? (includes Algorithm and Example)
- Implementing the Solution (Python code)
- Implementing the Solution (C++ code)
- How the Code works?
- Purpose of Shannon Fano coding
- Advantages and Disadvantages of Shannon Fano coding
What is a Shannon-Fano code?
A Shannon-Fano code is simply a method of encoding information.
Q.)So, how do we encode it?
Ans.) By using probabilities.
So we can define Shannon Fano Algorithm as a data compression "method of obtaining codes using probability."
The Shannon-Fano code was discovered almost simultaneously by Shannon and Fano around 1948. Also, the code created by the Shannon-Fano code is an instantaneous code . However, unlike the Huffman code , it is not necessarily a compact code.
How Shannon-Fano encoding works?
probability of occurrence
Occurrence probability is the probability that the symbol appears in the symbol string .
In this example,
aabbcddddd
Now let's see how the encoding actually works:
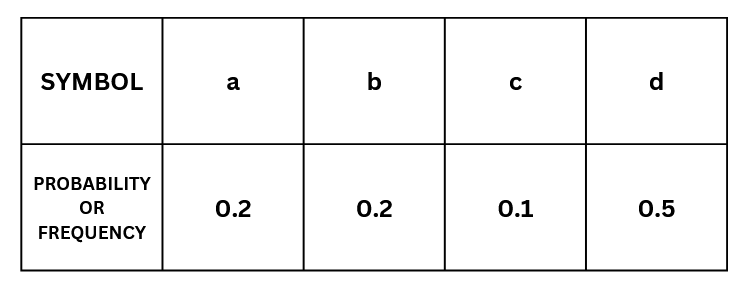
Step 1 Sort in descending order of probability of occurrence
First, sort the probabilities of each event in descending order .
In our example it would look like this:
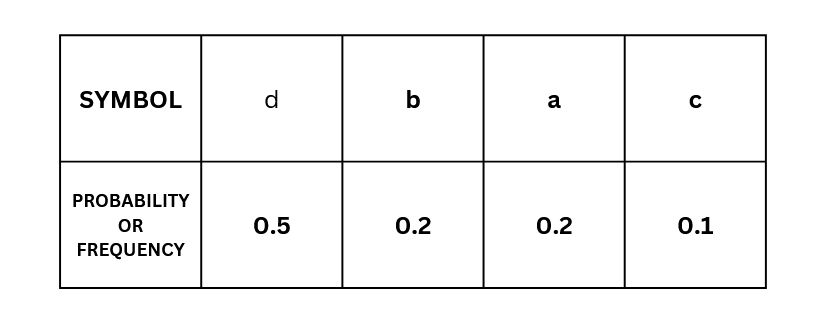
Here,
s1=d,
s2=b,
s3=a,
s4=c.
Step 2 Determine code length
The code length of each codeword using the formula we will continue to seek:
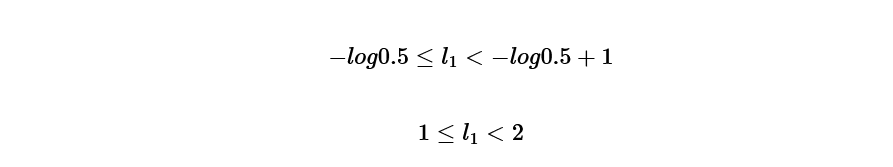
and from this formula called Kraft's inequality,
l(1)=1
Doing the same calculation for s2=b, s3=a, s4=c.

l2=3, l3=3, l4=4.
With this we obtained, d is one digit, b is 3 digits, a is 3 digits, c is 4 digits.
Step 3 Find the probability that is the basis of the code
Now that the code length has been determined, the next step is to determine the specific code.
first, P(1)=0, it is calculated as follows:
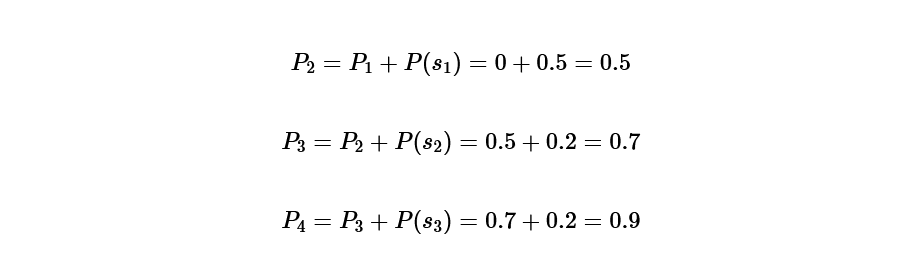
P(1)=0,
P(2)=0.5,
P(3)=0.7,
P(4)=0.9.
Step 4 Convert the probability obtained in step 3 into a binary number
Convert the calculated probabilities to binary.
Step 5 Determine the code according to the code length
Pay attention only to the binary number after the decimal point obtained in step 4, and match it with the length of the code length.
d is one digit,
b is 3 digits,
a is 3 digits,
c is 4 digits, so
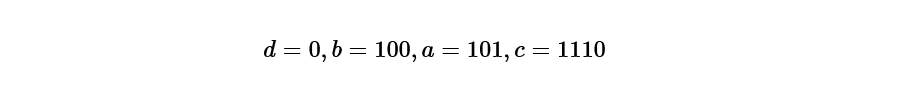
Conclusion
The higher the probability of occurrence, the shorter the code length.
If a code with a high probability of occurrence is associated with a code with a long code length, the data will be unnecessarily large.
Therefore, by associating a code with a shorter code length with a symbol with a higher probability of occurrence, communication can be performed efficiently.
Python Code - Shannon-Fano
class compress:
# Compress class for storing different parameters of string
def __init__(self, correspond):
self.original = correspond
self.count = 0
self.code = ""
self.probability = 0
class shannon_fennon_compression:
# Shannon Compression Class for compressing data using shannon fennon encoding
def __getProbability(self, compressor):
return compressor.probability
def compress_data(self, data):
'''
1- Process String and find probability of all the unique occurences of characters in String
2- Using processed list to store elements which are been processed ie... probability is been found
3- probability list consists of probability of each characters
'''
processed = []
compressor = []
total_length = len(data)
for i in range(len(data)):
if data[i] not in processed:
processed.append(data[i])
count = data.count(data[i])
# Finding probability of unique characters in data
var = count/total_length
comp = compress(data[i])
comp.count = count
comp.probability = var
compressor.append(comp)
# sorting probability in descending order
sorted_compressor = sorted(
compressor, key=self.__getProbability, reverse=True)
split = self.__splitter(
probability=[i.probability for i in sorted_compressor], pointer=0)
self.__encoder(sorted_compressor, split)
return sorted_compressor
# split probabilities in order used in shannon encoding
def __splitter(self, probability, pointer):
diff = sum(probability[:pointer+1]) - \
sum(probability[pointer+1:len(probability)])
if diff < 0:
point = self.__splitter(probability, pointer+1)
diff_1 = sum(probability[:point]) - \
sum(probability[point:len(probability)])
diff_2 = sum(probability[:point+1]) - \
sum(probability[point+1:len(probability)])
if abs(diff_1) < abs(diff_2):
return point-1
return point
else:
return pointer
# Encode string to compressed version of string data in binary
def __encoder(self, compressor, split):
if split > 0:
part_1 = compressor[:split+1]
for i in part_1:
i.code += '0'
if len(part_1) <= 1:
return
self.__encoder(part_1, self.__splitter(
probability=[i.probability for i in part_1], pointer=0))
part_2 = compressor[split+1:len(compressor)]
for i in part_2:
i.code += '1'
if len(part_2) <= 1:
return
self.__encoder(part_2, self.__splitter(
probability=[i.probability for i in part_2], pointer=0))
elif split == 0:
part_1 = compressor[:split+1]
for i in part_1:
i.code += '0'
part_2 = compressor[split+1:len(compressor)]
for i in part_2:
i.code += '1'
# Main Function
if __name__ == '__main__':
print("Data--- malyalam madman")
compressor = shannon_fennon_compression()
compressed_data = compressor.compress_data("malyalam madman")
for i in compressed_data:
print(
f"Character-- {i.original}:: Code-- {i.code} :: Probability-- {i.probability}")
print("")
print("Data--- shannon")
compressed_data = compressor.compress_data("shannon")
for i in compressed_data:
print(
f"Character-- {i.original}:: Code-- {i.code} :: Probability-- {i.probability}")
print("")
print("Data--- fennon")
compressed_data = compressor.compress_data("fennon")
for i in compressed_data:
print(
f"Character-- {i.original}:: Code-- {i.code} :: Probability-- {i.probability}")
C++ Code - Shannon-Fano
#include<iostream>
#include<bits/stdc++.h>
#include<vector>
#include<stdlib.h>
#include<math.h>
#include<fstream>
#include<windows.h>
using namespace std;
int actual;
class OP{
public:
int freq;
char ch;
string codw;
void getd()
{
cout<<"Enter Character:";cin>>ch;
cout<<"Enter Frequency:";cin>>freq;
this->codw="";
}
void getd(char dh,int preq)
{
this->ch=dh;
this->freq=preq;
this->codw="";
}
void display()
{
cout<<"Character:"<<ch<<" Frequency:"<<freq<<endl;
}
void cop()
{
cout<<"Code of "<<ch<<"="<<codw<<endl;
}
};
OP pi[127];
class chunks{
public:
string b8;
char d8;
int i8;
};
chunks cnks[500];
void shan(int s,int e)
{
if(s<e)
{
int sum_1=0,sum_2=0;
int mind=10000;
int t=0;
int diff=0;
int pt;
int i,j,k,cmp;
for(cmp=0;cmp<(e-s);cmp++)
{
for(k=s;k<=s+cmp;k++)
{
sum_1=sum_1+pi[k].freq;
}
for(j=s+cmp+1;j<=e;j++)
{
sum_2=sum_2+pi[j].freq;
}
diff=abs(sum_2-sum_1);
if(diff<=mind)
{
mind=diff;
pt=cmp+s;
}
sum_1=0;
sum_2=0;
}
for(i=s;i<=pt;i++)
{
pi[i].codw=pi[i].codw+"1";
}
cout<<endl;
for(i=pt+1;i<=e;i++)
{
pi[i].codw=pi[i].codw+"0";
}
int tmpp=pt;
shan(tmpp+1,e);
shan(s,tmpp);
}
}
void rdfile()
{
ifstream inFile;
char ch;
cout<<"Reading file = ab.txt";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
inFile.open("ab.txt");
if (!inFile)
{
cout << "The input file could not be opened."<<endl;
exit(0);
}
for(int i=0;i<127;i++)
{
cout<<"Char("<<i<<")="<<char(i)<<endl;
pi[i].getd(char(i),0);
}
ch = inFile.get();
while (ch != EOF)
{
pi[int(ch)].freq++;
ch = inFile.get();
}
}
void wtfile(int h)
{
ifstream inFile;
ofstream outfile;
outfile.open("1_Codeword.txt");
char ch;
cout<<endl;
cout<<"Reading file = ab.txt"<<endl;
cout<<"Generating 1_Codeword.txt file";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
inFile.open("ab.txt");
if (!inFile)
{
cout << "The input file could not be opened."<<endl;
exit(0);
}
ch = inFile.get();
int i;
while (ch != EOF)
{
i=h;
while(pi[i].ch!=ch)
{
i++;
}
outfile<<pi[i].codw;
ch = inFile.get();
}
outfile.close();
cout<<"File Generated!"<<endl;
}
int binTOdec(string binaryString)
{
int value = 0;
int indexCounter = 0;
for(int i=binaryString.length()-1;i>=0;i--)
{
if(binaryString[i]=='1'){
value += pow(2, indexCounter);
}
indexCounter++;
}
return value;
}
void dcp()
{
ifstream inFile;
ofstream outfile;
outfile.open("2_compressed.txt");
char ch;
cout<<"Reading 1_Codeword.txt file"<<endl;
cout<<"Generating 2_compressed.txt file.";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
inFile.open("1_codeword.txt");
if (!inFile)
{
cout << "The input file could not be opened."<<endl;
exit(0);
}
ch = inFile.get();
int i=0,lmt=0;
cout<<"\tCHAR\tINT\tBINARY\tCint"<<endl;
while (ch != EOF)
{
cnks[i].b8=cnks[i].b8+ch;
while(cnks[i].b8.length()!=8)
{
ch = inFile.get();
if(ch == EOF)
{
lmt++;
ch = '0';
}
cnks[i].b8=cnks[i].b8+ch;
}
// cnks[i].i8 = binTOdec(cnks[i].b8);
// cnks[i].d8 = char(cnks[i].i8);
cnks[i].d8 = char(binTOdec(cnks[i].b8));
cnks[i].i8 = int(cnks[i].d8);
cout<<"\t"<<cnks[i].d8<<"\t"<<cnks[i].i8<<"\t"<<cnks[i].b8<<"\t"<<int(cnks[i].d8)<<endl;
outfile<<cnks[i].d8;
ch = inFile.get();
i++;
}
actual = (i*8)-lmt;
outfile.close();
cout<<"\nFile 2_compressed.txt Generated!"<<endl;
Sleep(100);
}
void fina()
{
ifstream inFile; // input file
ofstream outfile; //output file
outfile.open("3_BinaryOfCompressed.txt");
char ch;
cout<<"Reading file = 2_Compressed.txt"<<endl;
cout<<"Generating 3_BinaryOfCompressed.txt file.";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
inFile.open("2_compressed.txt");
if (!inFile)
{
cout << "The input file could not be opened."<<endl;
exit(0);
}
ch = inFile.get();
int i=0;
cout<<"Results In 3_BinaryOfCompressed"<<endl;
cout<<"Character\tBinary"<<endl;
while(ch != EOF)
{
while (ch != EOF)
{
cout <<"\t"<< ch<<"\t"<<int(ch)<<"\t";
bitset<8> bin_x(ch);
outfile<<bin_x;
cout<<"binary ="<<bin_x<<endl;
ch = inFile.get();
cout<<"CHAR"<<ch<<"\t"<<int(ch)<<"\t\t";
}
ch = inFile.get();
}
cout<<"\nGenerated 3_BinaryOfCompressed.txt file!"<<endl;
Sleep(1000);
outfile.close();
}
void las(int h)
{
ifstream inFile;
ofstream outfile;
inFile.open("3_BinaryOfCompressed.txt");
outfile.open("4_Finalizedfile.txt");
cout<<"Reading file = 3_BinaryOfCompressed.txt"<<endl;
cout<<"Generating 4_Finalizedfile.txt file.";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
Sleep(500);
cout<<".";
if(!inFile)
{
cout << "The input file could not be opened."<<endl;
exit(0);
}
char ch;
ch = inFile.get();
string str="";
for(int i=0;i<actual;i++)
{
str=str+ch;
for(int k=h;k<127;k++)
{
if(pi[k].codw==str)
{
outfile<<pi[k].ch;
str="";
}
}
ch = inFile.get();
}
outfile.close();
cout<<"\nGenerated 4_Finalizedfile.txt file!"<<endl;
}
void deta()
{
ifstream iff;
iff.open("ab.txt"); //enter Your input file path with name
iff >> std::noskipws;
char ch;
int siz=0;
while(iff>>ch)
{
siz++;
}
cout<<"\n\tFile Name\t|\tSize";
cout<<"\n\t ab.txt||\t"<<siz<<"bytes";
iff.close();
iff >> std::noskipws;
iff.open("2_compressed.txt"); //enter Your input file path with name
siz=0;
while(iff>>ch)
{
siz++;
}
cout<<"\n\t2_compressed.txt||\t"<<siz<<"bytes";
iff.close();
}
int main()
{
int i,j,k,n;
int sum_1=0,sum_2=0;
int mind=10000;
int t=0;
int diff=0;
int pt;
n=127;
rdfile();
for(i=0;i<n-1;i++)
{
for(j=0;j<n-i-1;j++)
{
if(pi[j].freq>pi[j+1].freq)
{
OP tmp;
tmp=pi[j];
pi[j]=pi[j+1];
pi[j+1]=tmp;
}
}
}
int h;
for(i=0;i<n;i++)
{
if(pi[i].freq!=0)
{
h=i;
break;
}
}
for(i=h;i<n;i++)
{
cout<<i;
pi[i].display();
}
shan(h,n-1);
ofstream codfile;//codeword file
codfile.open("codfile.txt");
for(i=h;i<n;i++)
{
codfile<<pi[i].ch<<" || Freq="<<pi[i].freq<<" || Codeword="<<pi[i].codw<<endl;
pi[i].cop();
}
codfile.close();
wtfile(h);
dcp();
cout<<"ACTUAL==================================================="<<actual<<endl;
fina();
las(h);
deta();
return 0;
}
The following codes helps us to fully implement implement Shannon Fano coding Algorithm.
How the Code works?
Idea implemented :
- Count the number of each symbol and make a frequency table.
- Sort the table in descending order of appearance frequency.
- Split the table vertically. At this time, the sum of appearance frequencies should be equalized as much as possible.
- Assign code 0 to the upper half symbol and code 1 to the lower half symbol.
- Apply steps 3 and 4 again to the two split parts and assign the next code. Repeat this operation until there is only one element in the table.
Purpose of Shannon Fano coding
Therefore, by associating a code with a shorter code length with a symbol with a higher probability of occurrence, communication can be performed efficiently .
Advantages and Disadvantages of Shannon Fano coding
Advantages :
-
Shannon-Fano codes are easy to implement using recursion.
-
Higher the probability of occurrence, the shorter the code length in Shannon Fano Coding.
-
For Shannon Fano coding we do not need to build the entire codeblock again and again. Instead, we simply obtain the code for the tag corresponding to a given sequence.
Disadvantages :
-
Shannon-Fano codes are not compact codes.
-
In Shannon-Fano coding, we cannot be sure about the codes generated. There may be two different codes for the same symbol depending on the way we build our tree.
-
Shannon Fanon coding is not a unique code. So in case of errors or loss during data transmission, we have to start from the beginning.
With this article at OpenGenus, you must have the complete idea of Shannon Fano coding.