Find the Largest lexicographic array with at most K consecutive swaps

Reading time: 30 minutes

For a given array, find the largest lexicographic array which can be obtained from it after performing K consecutive swaps. Given two arrays A1 and A2, A1 is defined to be lexicographically larger than A2 if for the first i (from 0 to length of smaller array), element at index i is greater than element at index i of A2.

Note you can do less than K swaps as forcing K swaps may reduce the largeness of the result array.

We will solve this using:

• a naive approach O(N!) time
• Greedy approach O(N^2) time

Example to understand the problem

Consider the following array:

A1 = [1, 33, 44, 11, 2, 5]
A2 = [1, 39, 20, 1, 0, 4]

A2 is lexicographically larger than A1 as for index 1, 39 > 33. 

A3 = [2, 99, 100]

A3 is lexicographically smaller than A1 and A2 as length of A3 is smaller than length of A1 and A2.

For the problem, consider this example:

A1 = [3, 5, 1, 4]

The lexicographically largest array is:
[5, 4, 3, 1]

With 1 consecutive swap, the largest lexicographically largest array is:
[5, 3, 1, 4]

With 2 consecutive swaps, the largest lexicographically largest array is:
[5, 3, 4, 1]

The lexicographically largest array for the input array is:

And, the lexicographically largest array after 1 consecutive swap is:

Naive Approach O(N!)

A naive approach would be to generate all permutations of the array and selecting the one which satisfies the condition of K consequtive swaps.
Generation of all permutations takes n! time.

The steps involved are:

1. Generate all permutations of the array.
2. Count the number of swaps.
3. If number of swaps is less than or equal to K, update lexicographically largest array.

Pseudocode:

Input: array[]
1. Generate all perumations of the array using some function(like next permutation)
2  Count the number of swaps: 
    (a)Loop through the length of the array and compare with original array.
3. If the current array is lexicographically larger than the array:
    (i)Update the array lexicograph_max[]

Algorithm O(N^2)

We implement a greedy approach which runs as long as the value of the counter variable for swaps is less than K and the array is not lexicographically largest.

The algorithm goes as follows:

1. Loop from the 0-th index of the array to the last index of the array as long as K is non-zero.
2. For each element, find the largest element in the array which is greater than the current element and can be swapped with the current element in at most K swaps.
3. Swap the found element with the current element and update the value of K.

Implementation

#include <bits/stdc++.h>

using namespace std;

int main()
{
    //Obtaining length of array and number of allowed swaps
    int n, k;
    cin >> n >> k;

    int a[n];

    //Taking input of array elements
    for(int i=0; i<n; i++){
        cin >> a[i];
    }

    //Swapping elements while k is non-zero
    for(int i=0; i<n-1 && k>0; i++){
        //Initializing temporary index to current index
        int in = i;

        for(int j=i+1; j<n; j++){
            //Break if max swaps are exceeded
            if(k<j-i) break;

            //Update maximum element index
            if(a[j]>a[in]){
                in = j;
            }
        }

        //Swap the elements from in to the i-th index
        for(int j=in;j>i;j--){
            swap(a[j], a[j-1]);
        }

        //Update k after swapping in-i elements
        k -= in-i;
    }

    //Printing lexicographically largest array
    for(int i=0;i<n;i++) cout << a[i] << " ";

    return 0;
}

Examples

//Console input
5 3
3 5 4 1 2
//Console output
5 4 3 2 1

Here is the state of the array for all iterations:

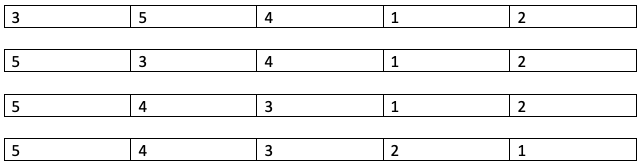
• In the first iteration, the first and second elements are swapped.
• In the second iteration, the second and third elements are swapped.
• In the third iteration, the fourth and fifth elements are swapped.

Complexity

The time complexity of this algorithm is O(N^2).