Machine dependent optimizations

Code optimization in compiler design is grouped into two major optimization techniques. These are machine-independent and machine-dependent. In this article, we learn about optimization involving the underlying machine.

Table of contents.

1. Introduction.
2. Peephole optimizations.
3. Instruction selection
4. Summary.
5. References.

Introduction.

Code optimization in compiler design is grouped into two major optimization techniques. These are machine-independent and machine-dependent. The former is applied to intermediate code while the latter is applied to object code.
Machine-dependent optimizations focus on the translation of code in a way that fully exploits the specifications of the underlying machine. It involves CPU registers, absolute memory, and references.

Peephole optimizations.

This refers to any optimization that looks at a small section of code narrowly, this could be two or three instructions, then makes focused changes within the examined section.

This optimization is easy to implement in the final stages of compilation although will have very little overall effect.

An example of a peephole optimization is; Redundant load elimination.
In Redundant load elimination, a sequence of expressions that modify and use similar variables can easily result in two adjacent instructions that save a register into memory, then immediately load the same value again.

For example;

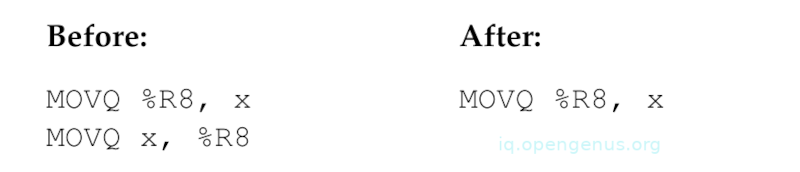
A variation is that a load to a different register can be converted into a direct move between registers, this saves unnecessary load and pipeline stall.

Instruction selection.

In a rich CISC instruction set, a single instruction can combine multiple operations such as dereferencing pointers, memory accesses, and arithmetic operations.
We can exploit these powerful instructions by using instruction selection by tree coverage.
The idea is to first represent each instruction in the architecture as a template tree whereby leaves are addresses in memory, constants, or registers that can be substituted into an instruction.

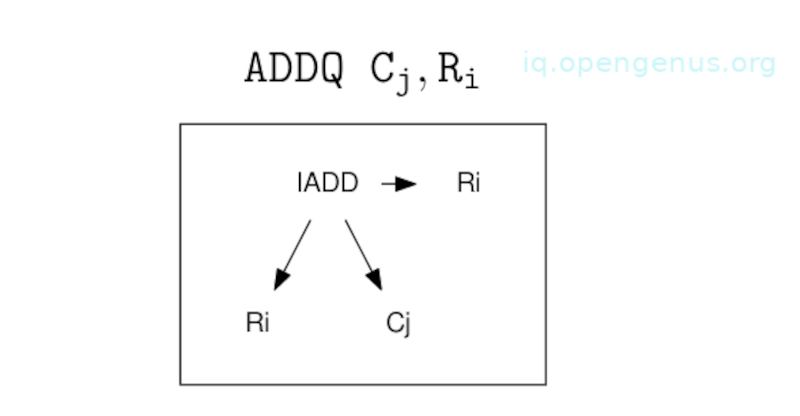
For example, a variant of the X86 ADDQ instruction can add two registers together. This is then used to implement an IADD node in the DAG as long as the leaves of IADD places the result in the same register as the second argument.
This is expressed as a tree fragment matching a part of the DAG and instruction to be emitted on the specified register numbers are chosen.

The following are examples of X86 instructions represented as tree templates.

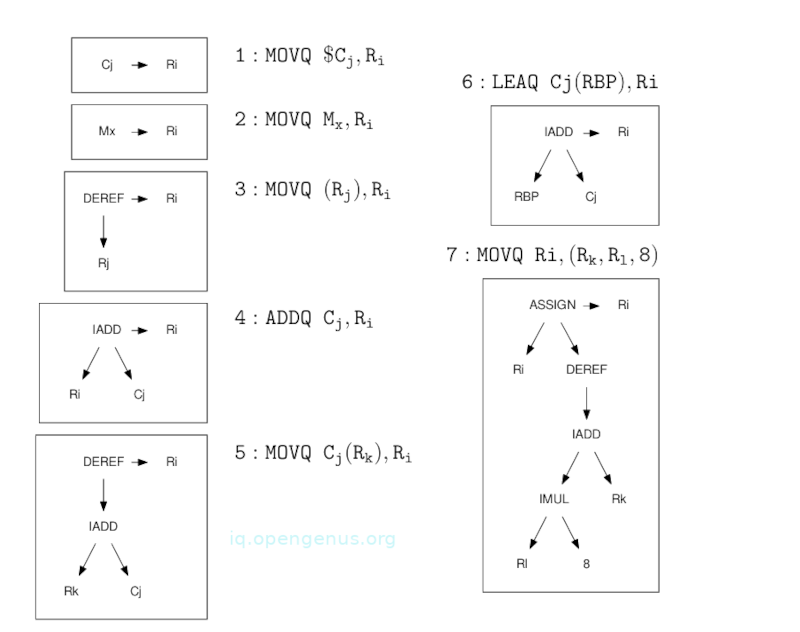
The simple instructions at the top substitute an entity in the DAG for another. MOV $Cj, Ri converts a constant into a register, and MOV Mx, Ri converts a memory location into a register.
Richer instructions have more structure, that is, the complex load MOV Cj(R1, 8), Ri can be used to represent a combination of add, multiply, and dereferencing.

The image above does not represent the entire X86 instruction set since to describe a significant subset requires hundreds of entries per instruction to capture multiple variations on each instruction.

Having a complete library of templates written, the task of the code generator is to examine the tree for subtrees matching an instruction template. When one is located, the corresponding instruction is emitted and the matching portion of the tree is replaced with the right side of the template.

For example, assuming we want to generate X86 code for the following statement;
a[i] = b + 1;
Suppose b is a global variable, a and i are local variables at positions 40 and 32 above the base pointer, respectively.
We have the following steps for tree rewriting.

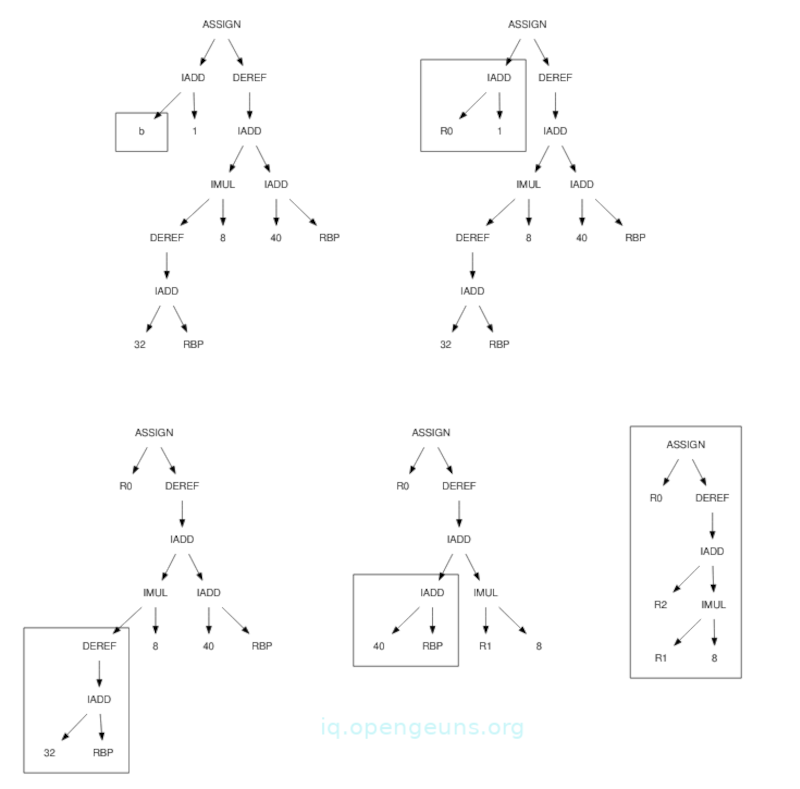
In each DAG above, we have a box that indicates the subtree matching a rule in the 4th image.

Steps

1. The left IADD is executed first to compute the value of the expression. In the table of templates, there is no IADD that directly adds a memory location to a constant, therefore, we select a rule (2) that emits the instruction MOVQ b, %R0 and converts the left side of the template(a memory location) into the right side(register %R0).
2. We see an IADD of a register and a constant that matches the template pf rule (4). We emit the instruction ADDQ, $1, %R0 and replace the IADD subtree with the register %R0.
3. We look at the other side of the tree and use rule (5) to match the entire subtree that loads the variable i from %RBP + 32 by emitting instruction MOVQ 32(%RBP), %R1 and replacing the subtree with register %R1.
4. Similarly we can use rule (6) to compute the address of a by emitting LEAQ 40(%RBP), $R2. Here, notice that this is in effect a three-address addition specialized for use with a register and the base pointer. Unlike rule number 4, it doesn't modify the source register.
5. Template rule (7) matches what is remaining. Here, e can emit MOVQ %R0, (%R2, %R1, 8) which stores the value in R1 into the computed array address of a. The left side of the template is replaced with the right side leaving the register %R0. The tree is completely reduced to a single register and thus code generation is complete therefore we can free register %R0.

Under a simple code generation scheme, the 16-node DAG produces 16 instructions of output. By using tree coverage we reduced the output to only five instructions listed below;
MOVQ b,%R0
ADDQ $1,%R0
MOVQ 32(%RBP),%R1
LEAQ 40(%RBP),%R2
MOVQ %R0,(%R2,%R1,8)

Summary.

Machine-dependent optimizations focus on the translation of code in a way that fully exploits the specifications of the underlying machine. It involves CPU registers, absolute memory, and references.

We have learned two machine-dependent optimization techniques, the first is peephole optimization techniques and instruction selection. The former involves looking at small sections of code narrowly and then making focused changes within the examined section while the latter involves exploiting rich CISC architecture by using a single instruction to perform multiple operations such as dereferencing pointers, memory accesses, arithmetic operations.

References.

1. Machine-idependent optimization.
2. Introduction to Compilers and Language Design - Douglas Thain