Algorithm to convert Hexadecimal to Binary

In this article, we have presented the basics of Hexadecimal and Binary representation and an algorithm to convert Hexadecimal to Binary.

Table of content

1. Definitions
2. Algorithm
3. Time & Space Complexity
4. A way of implementation

1. Definitions

In mathematics there are different numbers representations that belongs to a set, numerical, real, complex.

In informatics there are also different numbers representations: integers, float, double, char, user defined, and so on.

For all these ones, there must be a way that computers know which one belongs to.
Because a processor is an electronic component and there are only positive and negative currents that flows into it, engineers come with the solution to assign a positive current with 1 and with no current charge with 0.

The next step was how to represent numbers, and here the base numbers representations were defined as

binary {0,1}
decimal {0,1,2,3,4,5,6,7,8,9}
hex {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}

As we can see a general rule for any base set is given by the formula

base(n) = {0..n-1}

Humans work with decimals, computers work with binary and colors work with hex.
You might notice in any digitally painter program the representation of a color code consist in 6 hex numbers, for ex.:

black hex code is 000000 equiv decimal code is (0,0,0)
white hex code is FFFFFF equiv decimal code is (255,255,255)

Meaning for a maximum representation number 255 it was assigned 2 hex numbers of F as we could calculate in the next example:

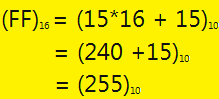
or by using the binary base equivalent:

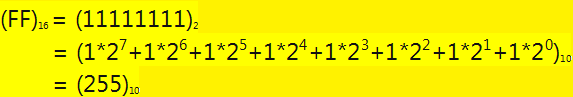
2. Algorithm

The algorithm is slightly different from the above example, meaning will need to extract the rest from the hex number as long as the divisor is different than 0.

The steps to convert Hexadecimal to Binary are:

1. Get input in hexadecimal. Initialize answer as ans = "".
2. If input > 0, go to step 3 else go to step 5
3. Get binary literal tmp1 = input % 2; tmp1 is 0 or 1. Append tmp1 to front of ans.
4. Update input to input / 2 (Integer part only). Go to step 2.
5. Print answer ans. (ans is in binary)

    for each hex in string
    do {
        binary = hex mod base;
        hex = hex / base;
        append binary to the binary array
    }
    while (hex != 0 );

Example:

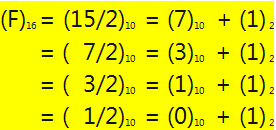
3. Time & Space Complexity

Since the highest number in hex is 15, the total numbers of operations for dividing the number is maximum 4. Hence the hex array is n, the total number of operations is 4*n which means time complexity is O(n);

Same case with space complexity since we've got n hex elements multiply by 4 binary elements.

4. A way of implementation

The following code is for C++ language and requires calls for strlen and strcat functions.

#include <iostream>
#include <string.h>

using namespace std;

const char *HEX = "0123456789ABCDEF";
const int BINARY = 2;

int getIndexHex(char hex)
{
    int i = 0, found = -1;
    
    while(HEX[i])
        if (HEX[i] == hex ) {found = i; break;} 
        else i++;
    
    return found;
}

char* toBase(int a, const int base)
{
    char *v, t;
    int c = a, d, i=0;
    
    v = new char[4];
    
    if (a>=0 && a < 16)
    do {
        d = c % base;
        c = c / base;
        v[i++] = '0' + d; //conversion from char to int
    }
    while (c != 0 );
    
    while(i<4)
        v[i++] = '0'; //fill in empty cells with zeros
        
    for (i=0;i<4/2;i++) // reverse array
        {
            t = v[i]; 
            v[i] = v[3-i];
            v[3-i] = t;
        }

    return v;
}
char* hexToBinary(const char *v )
{
    char *b = new char[ 4 * strlen(v) ];
    int i = 0;
    while(v[i])
        strcat(b , toBase( getIndexHex(v[i++]) , BINARY ) );

    return b;
}
int main()
{
    const char* b1 = "F0F0F0";
    cout<<b1<<endl;

    char* b2 = hexToBinary(b1);
    cout<<b2;
   
    return 0;
}

Output:

F0F0F0
111100001111000011110000

Notice that the above example requires input only for uppercase letters. As an exercise you can try to modify the script to accept lowercase scenario.

With this article at OpenGenus, you must have the complete idea of Algorithm to convert Hexadecimal to Binary.