
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes
Given an array A containing N integers, we perform M queries. Each query has three values START, END and a value D. For each query, the problem is to increment the values from the start to end index(both inclusive) in the given array by the given value d. A naive solution of leaping from start to end for each query is not feasible which takes O(NM) time whereas the efficient algorithm takes O(N+M) time complexity.
Naive approach O(N * M)
In the naive approach, we can traverse through the original array from index start to end and update every element by adding d. In this case, the time complexity of every query will be O(N) and the overall time complexity will be O(N * M).
Pseudocode:
for each query:
loop from start to end:
increment each element by d
We can improve this and solve the complete problem in O(N) time complexity
Algorithm O(N + M)
We create an array of the same size n and initialize all its elements to 0
Then, for each query i, we increment element at index start by d and decrement element at index end by d.
After all the queries are completed, we loop from 1 to n-1 in temp and increment each element by the element at its previous index.
Finally, we loop from 0 to n-1 and increment each element of a by its corresponding value in temp
The required array after modification is obtained
Example
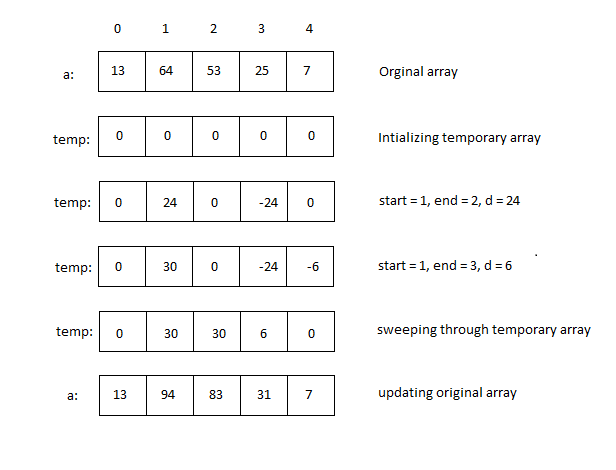
Complexity
Naive approach:
- Time Complexity: O(N * M)
- Auxiliary Space: O(1)
Efficient approach:
- Time Complexity: O(N + M)
- Auxiliary Space: O(N)
where
- N is the number of elements in the original array
- M is the number of updates
Implementation
#include <bits/stdc++.h>
#define MAXN 10001
using namespace std;
int main()
{
int n, m;
int a[MAXN], temp[MAXN];
//Obtaining input for number of elements and number of queries
cin >> n >> m;
//Forming the array a
for(int i=0;i<n;i++){
cin >> a[i];
}
//initializing temporary array to 0
for(int i=0;i<n;i++){
temp[i] = 0;
}
//performing the m queries
for(int i=0;i<m;i++){
int start, end, d;
cin >> start >> end >> d;
//incrementing start index by d
temp[start] += d;
//decrementing end+1 index by d
temp[end+1] -= d;
}
for(int i=1;i<n;i++){
//sweeping through the temporary array to obtain final value changes
temp[i] += temp[i-1];
}
for(int i=0;i<n;i++){
//updating the original array
a[i] += temp[i];
}
//displaying resultant array
for(int i=0;i<n;i++){
cout << a[i] << " ";
}
return 0;
}
Applications
- This algorithm can be used to find the updated element values of an array after multiple varying range-increments.
