Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 5 minutes
Given n and k, we will calculate permutation coefficient using dynamic programming in O(N * K) time complexity.
If we solve this problem using naive algorithm then time complexity would be exponential but we can reduce this to O(n * k) using dynamic programming. In this article, first of all we will visit the idea of Permutation coefficient, explore the naive approach and then, go into the dynamic programming approach to solve this efficiently.
What is Permutation Coefficient?
Permutation refers to the process of arranging all members of a given set to form a sequence.In case of permutation,order of elements is also considered.To understand the permutation,let's take an example: Examine all the different ways in which a pair of objects can be selected from five distinguishable objects - A,B,C,D,E.If both the letters selected and order of selection are considered,then the following 20 outcomes are considered :
AB BA AC CA AD
DA AE EA BC CB
BD DB BE EB CD
DC CE EC DE ED
Each of these 20 possible selections is called a permutation.They can be called as permutations of five objects taken two at a time.
The number of permutation on a set of n elements is given by n!
here, n! = n * (n-1) * (n-2) ... 1
The permutation coefficient is represented by P(n,k). It is used to represent the number of ways to obtain an ordered subset of k elements from a set of n elements.
P(n,k) = n.(n-1).(n-2)...(n-k+1)
= n!/(n-k)!
- P(n,k) = 1 if k=0
- P(n,k) = 0 if k>n
Example:
P(5,2) = 5!/(5-2)!
= 5!/3!
= 5.4
= 20
Note
- 0! = 1
- 1! = 1
Naive Approach:
The value of P(n,k) can be recursively calculated using the below recursive formula:
P(n,k) = P(n-1, k) + k * P(n-1, k-1)
The idea to implement the above recursive relation using a recursion function with base conditions. Following is the pseudocode:
int permutationCoeff(int n,int k)
{
if(k == 0) return 1;
if(k > n) return 0;
return (k*permutationCoeff(n-1,k-1)+permutationCoeff(n-1,k));
}
Implementation of Naive approach:
#include<bits/stdc++.h>
using namespace std;
//Returns value of P(n,k)
int permutationCoeff(int n,int k){
//Base cases
if(k==0){
return 1;
}
if(k>n){
return 0;
}
//Recursive call
return (k*permutationCoeff(n-1,k-1)+permutationCoeff(n-1,k));
}
int main(){
int n=5,k=2;
cout<<"Value of P("<<n<<", ""<<k<<") is "<<permutationCoeff(n,k);
return 0;
}
Output:
Value of P(5,2) is 20
Time Complexity of above code is O(2^k)
Basic Idea of using Dynamic Programming:
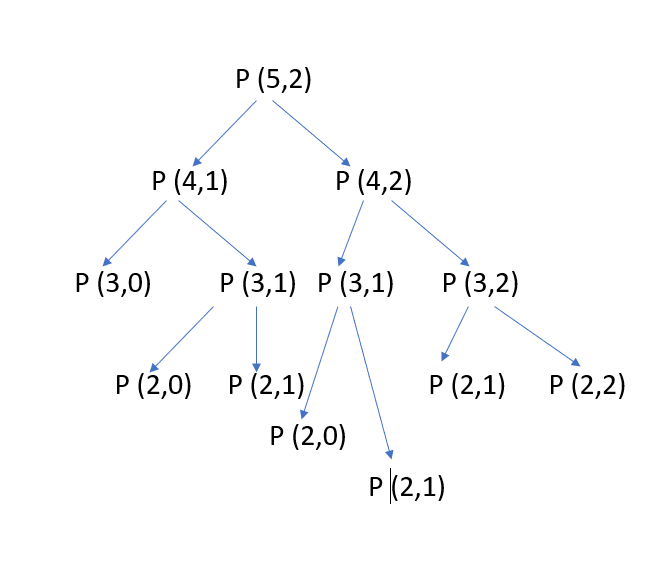
The above function is computing the same subproblems again and again. See the following recursive tree for n=5 and k=2:
The function P(3,1) is called two times,P(2,1) is called three times.For large values of n, there will be many subproblems which are being called again and again.The re-computation of subproblems can be avoided by applying dynamic programming techniques.
To do this, we will compute permutation coefficient in a bottom up manner and store all values in an array to avoid recursion calls.
Pseudocode:
int permutationCoeff(int n,int k)
{
int P[n+1][k+1];
for(int i=0;i<=n;i++)
{
for(int j=0;j<=min(i,k);j++)
{
if(j==0) P[i][j] = 1;
else P[i][j] = P[i-1][j] + j * P[i-1][j-1];
P[i][j+1]=0;
}
}
return P[n][k];
}
Implementation of Dynamic Programming approach:
#include<bits/stdc++.h>
using namespace std;
//Returns value of P(n,k)
int permutationCoeff(int n,int k){
int P[n+1][k+1];
for(int i=0;i<=n;i++){
for(int j=0;j<=min(i,k);j++){
//Base Cases
if(j==0){
P[i][j]=1;
}else{
P[i][j]=P[i-1][j]+j*P[i-1][j-1]; //calculating value using previously stored value.
}
P[i][j+1]=0;
}
}
return P[n][k];
}
int main(){
int n=5,k=2;
cout<<"Value of P("<<n<<", ""<<k<<") is "<<permutationCoeff(n,k);
return 0;
}
Output:
Value of P(5,2) is 20
Complexity
-
Time Complexity is O(n * k) ( As two consecutive loops are running. )
-
Space Complexity is O(n * k) ( To store the result,a 2d array is being used. )