Pumping Lemma For Context Free Languages

The pumping lemma is used as a way to prove if a language is context-free or not. In this article we have discussed this lemma for CFLs.

Table of contents.

1. Introduction.
2. Pumping lemma for context free languages.
3. Summary.
4. References.

Prerequisites.

1. chomsky normal form.

Introduction.

The pumping lemma is used as a way to prove if a language is context free or not.
There are two pumping lemmas one for regular languages and another for context free languages.

Here we discuss the latter, it states that for any CFL, it is possible to find two substrings that can be pumped any number of times and still turn out to be in the same language.

Pumping lemma for context free languages.

Theorem Let L be a context-free language, then there exists an integer p ≥ 1 referred to as the pumping length such that the following holds:
Every string s in L with |s| ≥ p can be written as s = uvxyz such that:

• |vy| ≥ 1, that is, v and y are not both empty.
• |vxy| ≤ p
• ${\mathrm{uv}}^{\mathrm{i}}{\mathrm{xy}}^{\mathrm{i}}\mathrm{z}$ ∈ L, for all i ≥ 0.

Proof: To prove the lemma we use the below resulting lemma about parse trees.

Lemma: 1 Let G be a context-free grammar in chomsky normal form, and s be a non-empty string in L(G), T a parse tree for s and l the height of T, that is, l is the total number of edges on the longest root-to-leaf path in T. Then |s| ≤ $2^{\mathrm{l}-1}$

Proof:
We prove this claim by induction on l by looking at its small values and using the fact that G is in chomsky normal form.

Now to start with proof of the pumping lemma. Let L be a context-free language and Σ and alphabet of L. By theorem 1 - (prerequisite article), there exists a context-free grammar in chomsky normal form G = (V,Σ, R, S) such that L = L(G).
We define r as the number of variables of G and p = $2^{\mathrm{r}}$. We will prove p's value can be used as the pumping length.
Consider an arbitrary string s in L such that |s| ≥ p and let T be a parse tree for s and l the height of T. By lemma 1 we have
|s| ≤ $2^{\mathrm{l}-1}$, on the other hand we have |s| ≥ p = $2^{\mathrm{r}}$

We combine these inequalities and we have $2^{\mathrm{r}}$ ≤ $2^{\mathrm{l}-1}$, that can also be written as l ≥ r + 1

Now consider the nodes on the longest path from root to leaf in tree T. This path has l edges and l + 1 nodes. The first l nodes store variables denoted by ${\mathrm{A}}_0$, ${\mathrm{A}}_1$, ... , ${\mathrm{A}}_{\mathrm{l-1}}$ where ${\mathrm{A}}_0$ = S and the last leaf node denoted by a stores a terminal.

Since l − 1 − r ≥ 0, the sequence ${\mathrm{A}}_{\mathrm{l-1-r}}$, ${\mathrm{A}}_{\mathrm{l-1}}$, ..., ${\mathrm{A}}_{\mathrm{l-1}}$ of variables is well defined and consists of r + 1 variables and since the number of variables in grammar G is equal to r, using the pigeon-hole principle it implies that there is a variable that occurs at least twice in this sequence, that is, there are indices j an k such that ℓ − 1 − r ≤ j < k ≤ l - 1 and ${\mathrm{A}}_{\mathrm{j}}$ = ${\mathrm{A}}_{\mathrm{k}}$

An illustration:

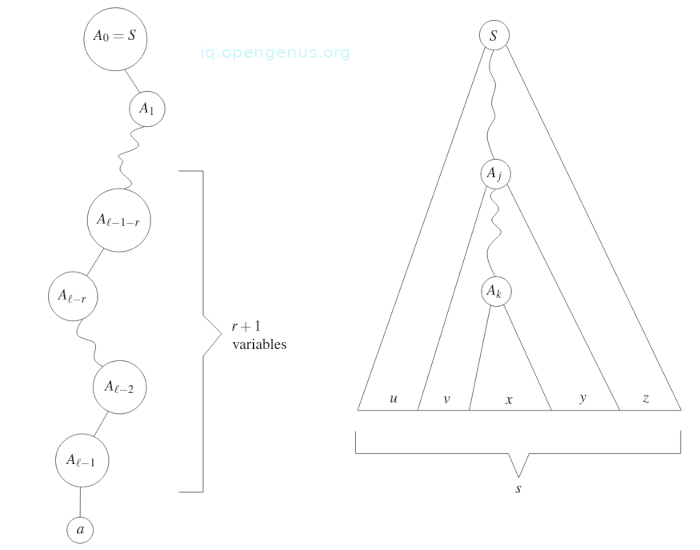
Recall T is a parse tree for string s, and thus terminals stored at the leaves of T ordered from left to right will form the string.
As we can see from the image above, nodes storing variables ${\mathrm{A}}_{\mathrm{j}}$ and ${\mathrm{A}}_{\mathrm{k}}$ divide s into five substrings, these are u, v, x, y, z such that s = uvxyz

Now we have to prove that the properties as stated in the pumping lemma hold.
For this we start with the third property, that is, proof that,
${\mathrm{uv}}^{\mathrm{i}}{\mathrm{xy}}^{\mathrm{i}}\mathrm{z}$ ∈ L, for all i ≥ 0.

In grammar G we have (1). S $\stackrel{*}{\Rightarrow }{\mathrm{uA}}_{\mathrm{jz}}$

Since ${\mathrm{A}}_{\mathrm{j}}\stackrel{*}{\Rightarrow }{\mathrm{uA}}_{\mathrm{ky}}$ and ${\mathrm{A}}_{\mathrm{k}}$ = ${\mathrm{A}}_{\mathrm{j}}$ we have (2). ${\mathrm{A}}_{\mathrm{j}}$ $\stackrel{*}{\Rightarrow }$ ${\mathrm{uA}}_{\mathrm{jy}}$.

And since, ${\mathrm{A}}_{\mathrm{k}}$ $\stackrel{*}{\Rightarrow }$ x and ${\mathrm{A}}_{\mathrm{k}}$ = ${\mathrm{A}}_{\mathrm{j}}$ we have (3). ${\mathrm{A}}_{\mathrm{j}}$ $\stackrel{*}{\Rightarrow }$ x.

From (1) and (3), it follows that
S $\stackrel{*}{\Rightarrow }$ ${\mathrm{uA}}_{\mathrm{jz}}$ $\stackrel{*}{\Rightarrow }$ uxz. The above implies that string uxz is in language L.

In general for each i ≥ 0, string ${\mathrm{uv}}^{\mathrm{i}}$${\mathrm{xy}}^{\mathrm{i}}$z is in language L since
S $\stackrel{*}{\Rightarrow }$ ${\mathrm{uA}}_{\mathrm{jz}}$ $\stackrel{*}{\Rightarrow }$ ${\mathrm{uv}}^{\mathrm{i}}$${\mathrm{A}}_{\mathrm{j}}{\mathrm{y}}^{\mathrm{i}}\mathrm{z}$$\stackrel{*}{\Rightarrow }$ ${\mathrm{uv}}^{\mathrm{i}}$${\mathrm{xy}}^{\mathrm{i}}$z.

With the above we have proved that the third property of the pumping lemma holds.

The next step is to prove the second property - (|vxy| ≤ p) also holds.
For this we consider a subtree rooted at a node storing ${\mathrm{A}}_{\mathrm{j}}$ and the path from this node to a leaf storing a terminal a is the longest path in this subtree.
Moreover, this path consists of l - j edges.
${\mathrm{A}}_{\mathrm{j}}\stackrel{*}{\Rightarrow }\mathrm{uxy}$ therefore this subtree is a parse tree for string uxy, where ${\mathrm{A}}_{\mathrm{j}}$ is the start variable.

By lemma 1, we conclude |vxy| ≤ ${\mathrm{2}}^{\mathrm{l-j-1}}$.

We know l − 1 − r ≤ j which is also l − j − 1 ≤ r, therefore |vxy| ≤ ${\mathrm{2}}^{\mathrm{l-j-1}}$ ≤ $2^{\mathrm{r}}$ = p.

We show that the first property in the pumping lemma holds by proving |vy| ≥ 1
Recall ${\mathrm{A}}_{\mathrm{j}}$ $\stackrel{*}{\Rightarrow }$${\mathrm{vA}}_{\mathrm{ky}}$

Let the first rule for this derivation be ${\mathrm{A}}_{\mathrm{j}}$ → BC, then ${\mathrm{A}}_{\mathrm{j}}$⇒ BC $\stackrel{*}{\Rightarrow }$ ${\mathrm{uA}}_{\mathrm{ky}}$.

Now note BC is a string of length two. Also by applying the rules of a grammar in chomsky normal form, strings cannot be shorter and therefore we have |${\mathrm{uA}}_{\mathrm{ky}}$| ≥ 2 which implies |vy| ≥ 1 and this completes the pumping lemma proof.

Summary.

The pumping lemma proves if a language is context-free or not.

There exists two pumping lemmas one for regular languages where if a language is regular it will always satisfy the lemma and the other for context free languages which we have discussed here.

References.

1. Pumping lemma for regular languages