
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will learn about how we can search for a particular element in a sorted 2D matrix.
Table of contents:
- What is a sorted 2D matrix?
- Problem we are trying to solve
- Approaches to solve problem
- How to solve problem using Binary Search method
- Use of Binary Search method in real life
- Final question
Pre-requisites:
- Binary Search
- Search element in rotated sorted array
- Finding 2 elements with difference k in a sorted array
Let us get started with how we can search for a particular element in a sorted 2D matrix.
What is a sorted 2D matrix?
For this article, we will be looking at a sorted 2D matrix that is sorted in ascending order (least to greatest order). This matrix will have N number of columns and M number of rows. In the example, we will have a 2D matrix with N = 4 columns and M = 3 rows.
The following is a visual representation of our example 2D matrix:
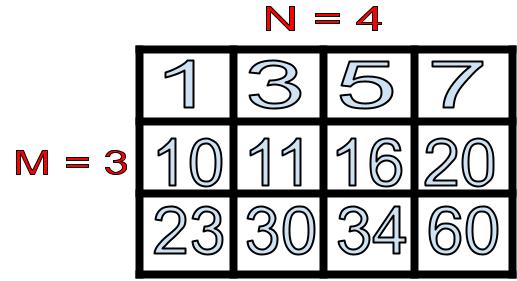
From this diagram we can see the that elements in each row are sorted from least to greatest (left to right). We can also see that the first element of each row is greater than the last element of the previous row. For example, 10 is the first element in the second row and it is greater than 7 which is the last element of the previous row. Similarly, 23 is greater than 20.
Problem we are trying to solve
We know that our matrix is sorted from least to greatest. We also know that there are 4 rows and 3 columns in this particular matrix. We have also learned about a pattern in which the first element of each row is greater than the last element of the previous row. How can we utilize what we know so far to find an element in the sorted 2D matrix?
Approaches to solve problem
The following are two approaches to solving this problem:
- Binary Search method
How to solve problem using Binary Search method
If a particular matrix like the one we went over above is inputed into a program. Our algorithm will search for a particular target element in this matrix and return true if the element is present, false if not present. In order to acheive this we can utilize an algorithm called Binary Search method. This method has a time complexity of O(log N).
The following is what our program will look like if element is present or not present:
input:
arr[][] = [[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 60]]
target = 41
output: true
explanation: 11 is present in our matrix, therefore we return true.
input:
arr[][] = [[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 60]]
target = 54
output: false
explanation: 54 is not present in out matrix, therefore we return false.
Let's go through the Binary Search method step by step:
Comments in code will provide explanation of what is going on.
Step 1: Check if matrix is empty or not available.
class matrix:
def search_matrix(self, matrix: List[List[int]], target:int)->bool:
if not matrix or not matrix[0]: # if there is no matrix or if the matrix is empty we return false.
return false
Step 2: Find our row, and compare target value to first and last values in row.
row = 0 # assume row currently is at 0th index.
# iterate over each row using a range based for loop.
# check if smallest value or greatest value is our target, if it is, return true.
for r in range(len(matrix)):
if target == matrix[r][0] or target == matrix[r][-1]: # r row, 0th value or last value in row (-1)
return True
Step 3: Check if your target is greater than the range.
# check if target is greater than first element of matrix and last element of matrix.
elif target > matrix[r][0] and target < matrix[r][-1]
# if both true
row = r # change row value to r
break
Step 4: Look for our target element in row using binary search.
# look for element in row using left(l) and right(r) pointers.
l, r = 0, len(matrix[row]) - 1 # start pointers l and r at 0.
while l <= r: # check if left value is less then or = to right value
# if true, then find mid value
mid = l + (r - 1) // 2
# check if target == mid value
if target == matrix[row][mid]:
return True
# if target is > than mid value
elif target > matrix[row][mid]:
# move left pointer to the right
l = mid + 1
# if target less than mid value
else:
r = mid - 1 # move right pointer to left
return false # if target element not found
Use of binary search method in real life
- Finding an element in a array that is sorted.
- Dictionary, in order to find a target word.
- Figuring out the resource requirements for a large system.
- To find a particular page number in a book.
- To find a particular book in a collection of arranged books.
Question
What is the average time complexity of Binary Search given in the article?
With this article at OpenGenus, you must have a strong idea of how to Search an element in Sorted 2D matrix.
