
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this OpenGenus article, we will explore a problem (Finding 2 elements with difference k in a sorted array), and find various methods of solving the problem, based on varying complexity. While this problem itself might be of some merit, let us focus more on the underlying idea, which serves as the core to many other problems.
Note that the language used to show example codes is C++, because, I believe it is the most apt language for studying algorithms.
Problem Statement
Given a sorted array of length n, find pair of elements whose difference is k (a,b | a-b = k) and print these elements.
We have explored the following approaches:
- Brute force approach O(N^2) time
- Divide and Conquer approach O(N logN) time
- Efficient approach O(N) time
Overview of the Solution
This problem is basically a search problem. Let me put the problem in another way :
In a sorted array, find for each element
aof the array, search if there exists an elementa-kin the array.
Let us discuss the steps for the solution to this problem stepwise :
Step 1 : Loop through each element of the array
Step 2 : For each element, search ifa-kis there in the array using binary search.
Step 3 : If that element exists, then the 2 numbers(a,a-k)exist with difference k. Exit the loop.
Step 4 : If even on iterating all elements, no valid pair is found, then there doesn't exist 2 elements with difference k.
Special Case :
If k = 0, then, we need to check if element occours twice, as searched element for a is a-0 = a which is present atleast once in the array. So, we can argue that since a exists, and (a,a) is a valid solution, so answer is valid. But it really depends on how this case is to be handled in a specific case/implementation.
Brute force approach
Explanation Of Logic
Step 1: We loop through all elements of the array, and for any index
i, we search if k-ar[i] exists.
void display_pairs(int k,vector<int> &ar){
for(int x=0;x<ar.size();x++){
if(findElement(ar,k-ar[x]) == true){
// found element pair ar[x],k-ar[x]
}
}
}
Step 2 : We search for element
k-ar[x]in the array using linear search
bool findElement(vector<int> &ar,int a){
for(int x=0;x<ar.size();x++){
if(ar[x] == a){
return true;
}
}
return false;
}
In this method, we can check the difference for each pair of elements, and print the ones which equals k.
Code for the brute force approach is shown below.
#include<iostream>
#include<vector>
using namespace std;
void display_pairs(int k, vector<int> ar){
int len = ar.size();
for(int x=0;x<len;x++){
for(int y=0;y<len;y++){
if(x==y){
continue; // same elements
}
if(ar[x]-ar[y] == k){
cout << ar[x] << "," << ar[y] << endl;
}
}
}
}
int main(){
cout << "Enter size of array : ";
int n;
cin >> n;
cout << "Enter elements of array : ";
vector<int> ar(n);
for(auto &x : ar){
cin >> x;
}
cout << "Enter value of K :";
int k;
cin >> k;
display_pairs(k,ar);
}
Following is the output of the code written above.
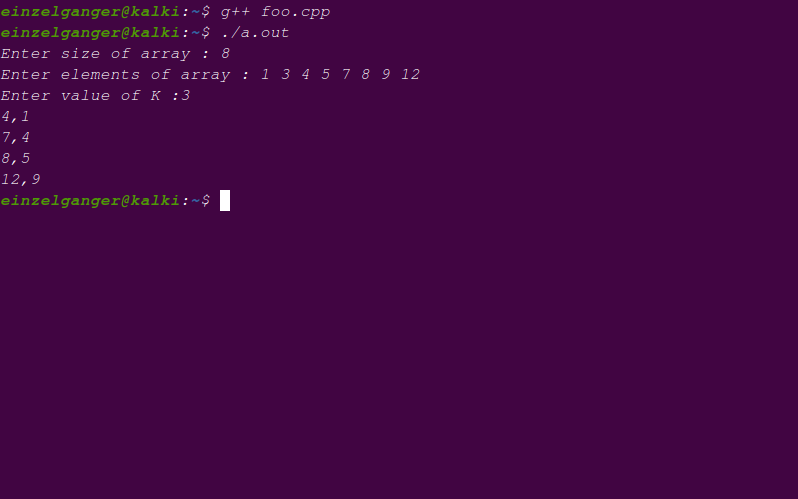
Note that the complexity of the code is O(n2) in the big O notation.
Divide and Conquer approach
We can notice, that the question is basically a search problem. For each element t in the list/array, we are searching for an element k-t in the array.
In the brute force approach we used linear search approach. We know, the most efficient search algorithm is divide and conquer based search or binary search. Using this, we can solve the problem more efficiently.
The steps are as follows:
- Step 1: We loop through all elements of the array, and for any index
i, we search if k-ar[i] exists. - Step 2 : We search for element
k-ar[x]in the array using binary search
Explanation Of Logic
NOTE : we are given an array which is already sorted. If not, sorting is easy using :
sort(ar.begin(),ar.end());
Step 1: We loop through all elements of the array, and for any index
i, we search if k-ar[i] exists.
void display_pairs(int k,vector<int> &ar){
for(int x=0;x<ar.size();x++){
if(findElement(ar,k-ar[x]) == true){
// found element pair ar[x],k-ar[x]
}
}
}
Step 2 : We search for element
k-ar[x]in the array using binary search
bool findElement(vector<int> &ar,int a){
int max = ar.size()-1,min=0,mid;
while(max>=min){
mid = (max+min)/2;
if(ar[mid] == a){
return true;
}
else if(ar[mid] < a){
min=mid+1;
}
else{
max = mid-1;
}
}
return false;
}
Notice that binary search can only work for sorted arrays, so we need to sort an unsorted array first, and then apply binary search. Luckily in our case, we already have a sorted array(given in the problem).
The code for binary search based solution to the problem is shown as follows :
#include<iostream>
#include<vector>
using namespace std;
int bin_search(vector<int> ar,int elt){
int min,max,mid;
min=0;
max=ar.size();
while(min <= max){
mid = (min+max)/2;
if(ar[mid] == elt){
return mid;
}
else if(ar[mid] > elt){
max = mid - 1;
}
else{
min = mid+1;
}
}
return -1; // element is not found
}
void display_pairs(int k, vector<int> ar){
int len = ar.size();
for(int x=0;x<len;x++){
int index = bin_search(ar,ar[x] - k);
if(index != -1){
cout << ar[x] << "," << ar[index] << endl;
}
}
}
int main(){
cout << "Enter size of array : ";
int n;
cin >> n;
cout << "Enter elements of array : ";
vector<int> ar(n);
for(auto &x : ar){
cin >> x;
}
cout << "Enter value of K :";
int k;
cin >> k;
display_pairs(k,ar);
}
The output of the code is shown below.
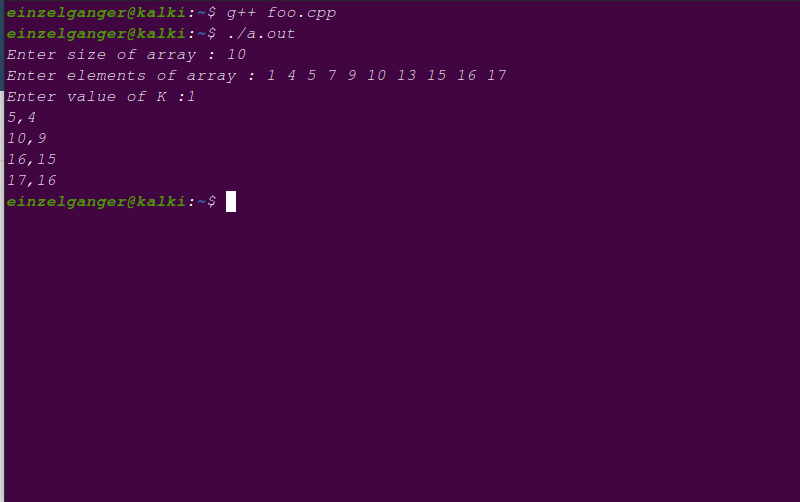
Question 1
What is the runtime complexity of the Binary Search based solution to the problem, shown above?
Attempt for better complexity
Warinig : Spoilers for the above question in this article below
Now, we have achieved complexity of O(n*log(n)) for the problem statement's solution. The question is, is there a better time complexity?
Notice that if we have a reasonable range of values, that any element of the list can take (ar[x]), that is, if it can take values small enough to create a list of all values it can take, then Yes, we can solve the problem in O(N).
Solution :: We reduce the search complexity to O(1) by making a boolean array that stores at index i true if element i is present in the list, and stores false if it is not present.
Now, the entire code will be same, just main function will be modified, and bin_search function will be changed.
Modified main function :
#include<iostream>
#include<vector>
#define r = 1000 // range is defined
using namespace std;
bool bucket_search(int elt, vector<bool> *pres){
if(elt+r < 0 or elt+r> pres.size()){
return false;
}
return pres[elt+r];
}
void display_pairs(int k, vector<int> &ar,vector<bool> &pres){
int len = ar.size();
for(int x=0;x<len;x++){
if(bucket_search(ar[x]-k,pres)){
cout << ar[x] << "," << ar[x] - k << endl;
}
}
}
int main(){
// range is from -r to r
cout << "Enter size of array : ";
int n;
cin >> n;
cout << "Enter elements of array : ";
vector<int> ar(n);
vector<bool> pres(2*r,false);
for(auto &x : ar){
cin >> x;
pres[x] = true;
}
cout << "Enter value of K :";
int k;
cin >> k;
display_pairs(k,ar,pres);
}
Note running this code will also yield same result.
A fun task : Find out the reason, the search function in the above code is bucket_search.
This implementation might seem good, but actually it is very bad. It consumes tremendous amount of memory, and although has a good time complexity, it has astonishingly bad memory complexity.
