Reading time: 35 minutes

Given two strings X and Y, the supersequence of string X and Y is such a string Z that both X and Y is subsequence of Z. in other words shortest supersequence of X and Y is smallest possible string Z such that all the alphabets of both the strings occurs in Z and in same order as of the original string.
Let's understand it with an example:

X = "opengenus"
Y = "operagenes"
shortest common supersequence of X and Y:
z = "openragenues"
and length of z is 12
we can see that both "opengenus" and "operagenes" is subsequence of "openragenues".

There can be more than one shortest common supersequence, in that case we may consider any of them as the lenght of the supersequence will be the same.

Here we will se two approachs to find the minimum lenght of common supersequence and also how to print a shortest common suersequence.

Algorithms

1. Recursive (Brute Force) approach

The method to find the shortest common supersequence is similar to that of finding the longest common subsequence. We start scanning from the left of both the string, if the current charecter matches then we add it to the supersequence and recur for the remaining strings (i.e. after skipping first charecter of both string). If the charecter doesn't matches then we take to cases, one when we add the cuurent charecter of first string to supersequence and recur for the remaining first string and complete second string, and the second is vice versa. Then we take the minimum length supersequence from the two.

As a base case when any of the string becomes empty we append the remaining string (if any) to the supersequence and return the same.

def shortestCommonSuper(str1, str2, scstr):
    if len(str1) == 0 or len(str2) == 0:
        scstr = scstr + str1[::-1] + str2[::-1]
        return scstr
    
    if str1[0] == str2[0]:
        return shortestCommonSuper(
            str1[1:], str2[1:], scstr + str1[0])
    else:
        scstr1 = shortestCommonSuper(
            str1[1:], str2, scstr + str1[0])
        scstr2 = shortestCommonSuper(
            str1, str2[1:], scstr + str2[0])
        return scstr1 if len(scstr1) < len(scstr2) else scstr2

The recursive approach takes O(2^min(m,n)) where m, n is length of the respective strings.

At each instance of the recursive function, we recur for at most 2 times and at each function call the string length is decreasing, so we have at most min(m, n) recursive calls. So overall time of the algorithm is O(2^{min(m, n)}) in the worst case.

2. Dynamic Programming approach

Before going to the dynamic programming approach, let's understand the recursive method a bit more by partial recursion tree of a problem:

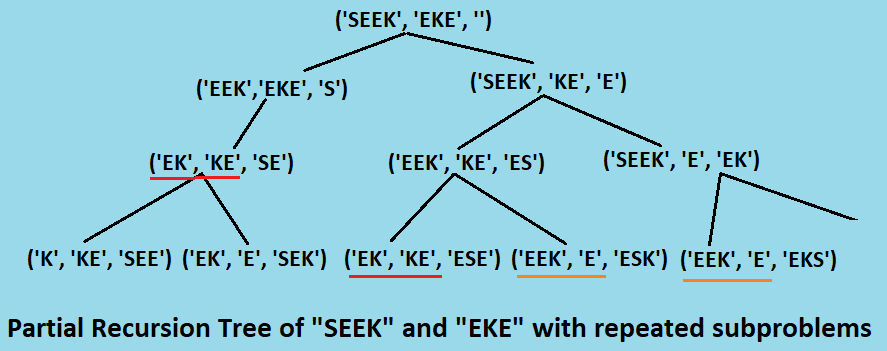
In the above partial tree we represented the repeated subproblems with same underlined colour bars. We can see that it already contains two repeated subproblems.

So the problem contains both repeated subproblems and optimal sub-structure property so we can solve it optimally with dynamic programming and memoization in O(m*n) time.

def shortestCommonSuperDP(str1, str2):
    dp = [[None for _ in range(len(str2) + 1)] for _ in range(len(str1) + 1)]
    for i in range(len(str1)+1):
        for j in range(len(str2)+1):
            if not i:
                dp[i][j] = j
            elif not j:
                dp[i][j] = i
            elif str1[i - 1] == str2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
            else:
                dp[i][j] =1 + min(dp[i - 1][j], dp[i][j - 1])

    return sc_len = dp[len(str1)][len(str2)]
    # for printing purpose
    #######

Implementations

Code in python3

import sys

def shortestCommonSuperDP(str1, str2):
    dp = [[None for _ in range(len(str2) + 1)] for _ in range(len(str1) + 1)]
    for i in range(len(str1)+1):
        for j in range(len(str2)+1):
            if not i:
                dp[i][j] = j
            elif not j:
                dp[i][j] = i
            elif str1[i - 1] == str2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
            else:
                dp[i][j] =1 + min(dp[i - 1][j], dp[i][j - 1])

    sc_len = dp[len(str1)][len(str2)]
    # for printing purpose
    scstr = [ None for _ in range(sc_len)]
    i, j = len(str1), len(str2)

    while i > 0 and j > 0 :
        if str1[i - 1] == str2[j - 1]:
            scstr[sc_len - 1] = str1[i - 1]
            i -= 1
            j -= 1
            sc_len -= 1
        
        elif dp[i][j - 1] < dp[i - 1][j]:
            scstr[sc_len - 1] = str2[j - 1]
            j -= 1
            sc_len -= 1
        else:
            scstr[sc_len - 1] = str1[i - 1]
            i -= 1
            sc_len -= 1
    while i > 0:
        scstr[sc_len - 1] = str1[i - 1]
        i -= 1
        sc_len -= 1
    while j > 0:
        scstr[sc_len - 1] = str2[j - 1]
        j -= 1
        sc_len -= 1        

    scstr = "".join(map(str, scstr))
    return scstr

str1 = "AGGTAB"
str2 = "GXTXAYB"
scstr = shortestCommonSuperDP(str1, str2)
print("Length of the shortest common supersequence is:", len(scstr))
print("Shortest common supersequence is:", scstr)

Output

Length of the shortest common supersequence is: 9
Shortest common supersequence is: AGXGTXAYB

Complexity

Time Complexity

• The recursive brute force approach takes O(2^{min(m, n)}) time.
• The Dynamice programming approach takes O(m*n) time. Where m, n are the length of the first and second string respectively.

Space complexity

• The Recursive approach takes O(m+n) auxiliary space, and stack space.
• The Dynamic Programming approach takes O(m*n) auxiliary space.