In this article, we have solved the problem "Shortest Unsorted Continuous Subarray" and explained the logic behind it and what are the different methods (like Monotonic Stack) we can use to solve it efficiently.

Table of content:

1. Problem Statement: Shortest Unsorted Continuous Subarray
2. Approaches to solve it
   3. Brute Force Method
   4. Using Monotonic Stack
   5. Comparing with Sorted Array
3. Conclusion

Problem Statement: Shortest Unsorted Continuous Subarray

Given an integer array nums, you need to find one continuous subarray that if you only sort this subarray in ascending order, then the whole array will be sorted in ascending order.

Return the shortest such subarray and output its length.

First, let's try to understand what's the question is and what we need to do. Given an array, we need to find a subarray from it such that if we sort this subarray the whole array becomes sorted. And another important thing to note is that the word "Continuous", which means the elements must be next to one another not be discontinuous, take a look at the image below.

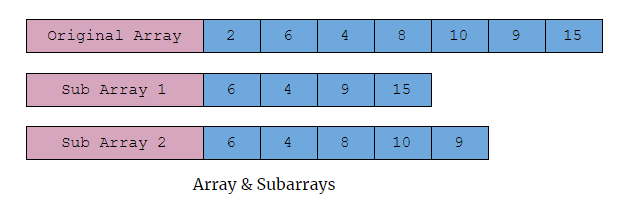
In the above example, both Sub Array 1 and Sub Array 2 are valid subarrays of the original arrays, but Sub Array 1 is not a Continuous subarray while Sub Array 2 is a continuous subarray.

And as we can see when we sort the subarray 2, the whole original array gets sorted hence the subarray 2 is the shortest Unsorted Continuous Subarray for the given array.

Now, Since we have got the idea of what we need to do, let's jump right into the code.

Approaches to solve it

The code for any question can be written in multiple ways, but we need to choose the most optimal solution so that our code works for large inputs and also our code remains fast.

We will see the 3 different ways in which we can solve this problem

1. Brute Force method
2. Using Monotonic Stack
3. By comparing with a sorted list

let's see them one by one.

1. Brute Force Method

In this method, we just use while loops & variables to check if the sub-array is sorted or unsorted and if the sub-array is unsorted it returns the index of the subarray.

Steps

1. Check if the array is already sorted.
2. From the start, check if the current element is smaller than all the elements ahead of it.
   • If true, move to the next element
   • Else break the loop
3. From the end, check if the current element is larger than all the elements behind it.
   • If true, move to the next element
   • Else break the loop
4. Finally, return the length of the shortest unsorted contiguous array

Take a look into this code,

def findUnsortedSubarray(nums):

    # returns 0 if the array is already sorted
    if nums == sorted(nums) : return 0  

    # we initiate two variables for the start and the end of the sub array

    n = 0            # start index
    m = len(nums)-1  # end index

    # A while loop that checks for the start of the unsorted subarray
    while n+1 < len(nums) and min(nums[n:]) == nums[n] :
        n+=1

    # A while loop that checks for the end of the unsorted subarray
    while m >= 0 and max(nums[:m+1]) == nums[m] :
        m-=1

    # returns the length of the Shortest Unsorted Continuous Subarray
    return len(nums[n:m+1])

.
In the above code, we have used 2 while loops. What happens in these while loops is that it checks if the current element is in the correct sorted position and it moves on to the next element, when the element is unsorted it breaks the while loop and gives us the required index.
And finally, we return the length of the Shortest Unsorted Continuous Subarray.

The time complexity of this algorithm is O(n^2) because for every iteration of the while loop we will traverse through the array and check if the element is in the sorted position.

The space complexity of this algorithm is O(n), where n is the size of the array nums.

Let's take a look at the memory usage and the time taken by this code to solve the problem.

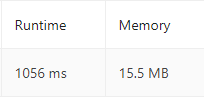
We can clearly see that this code takes a lot of time, hence it will be a problem if we pass very large arrays as input. So let's try a more efficient solution.

2. Using Monotonic Stack

A monotonic stack is a special data structure that is very useful when solving range-query problems like this. Let's see what is a monotonic stack before we use it to solve the problem.

A monotonic stack is a special variation of the normal stack in which the data can be stored in only ascending or descending order. Since the stack stores data in a monotone increasing or decreasing order, we call it a monotonic stack. Other than that the monotonic stack works just like a normal Stack Data Structure.

We know that in a sorted array the values are going to be ascending from the start and descending from the end. Thus using this logic, we create 2 monotonic stacks to store the indexes. And when the monotone nature fails (i.e. when the array element is unsorted) we pop out the index and check for the element in the next index.

Steps

1. Start from the beginning of the array
   • Pop all the elements from the stack that are greater than the current element
     • Take the smallest index as the start index mi
   • Push the element into the stack
2. Start from the end of the array
   • Pop all the elements from the stack that are smaller than the current element
     • Take the largest index as the end index ma
   • Push the element into the stack
3. Finally, return the length of the smallest unsorted continuous subarray.

Take a look at this code,

def findUnsortedSubarray(nums):

    # Two monotonic stacks to store the indexes
    Mstack1 , Mstack2 = [] , []

    n = len(nums) # length of the array

    mi = n  # start index
    ma = 0  # end index

    # To find the start index of the shortest unsorted continuous subarray
    for i in range(n):
        while Mstack1 and nums[Mstack1[-1]] > nums[i] :
            mi = min(mi , Mstack1.pop())
        Mstack1.append(i)

    # To find the end index of the shortest unsorted continuous subarray
    for i in range(n-1,-1,-1):
        while Mstack2 and nums[Mstack2[-1]] < nums[i] :
            ma = max(ma , Mstack2.pop())
        Mstack2.append(i)

    # returns the length of the shortest unsorted continuous subarray
    return len(nums[mi:ma+1])

.
In this code, the monotonic stack is used to store the indexes. In the first set of loops, the for loop scans the element indexes from start to end and the while loop is used to check if the current element is smaller than the previous element if so we pop the bigger element indexes from the stack and store it into the variable mi and then finally we push the current index into the stack.

In the second set of loops, the same thing happens but with just a few changes. The for loop scans the element indexes from the end to the beginning. The while loop checks if the current element is larger than the previous element if so it pops it and stores it in the variable ma and then it finally pushes the current index into the stack.

We use the min() and max() function to find the start and the end index values and store it in the variables mi and ma. Then finally, we return the length of the smallest unsorted continuous subarray.

Now let's take a look at the time taken and the memory used by this code.

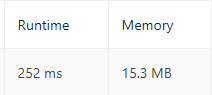
Now when we compare the runtime of this solution to the previous solution we can clearly see that this solution is way more faster than the previous one.

The time complexity of the algorithm is O(n), you may wonder this can happen since we have two loops one inside another. But when we look at it as a whole, each element is pushed into the stack only once and it will be popped only once, resulting in no redundant operations. Thus the time complexity depends only on the number of elements n present in the array.

The space complexity of the algorithm is also O(n), where n is the size of the array.

3. Comparing with Sorted Array

This method does what exactly it says, we create a new sorted array of the original array and now compare the elements between the new sorted array and the original array.

Steps

1. Create a new sorted array from the original array.
2. From the beginning compare each element of the sorted array with the element of the unsorted array
   • Break the loop if they are not equal
3. From the end compare each element of the sorted array with the element of the unsorted array
   • Break the loop if they are not equal
4. Finally return the length of the Shortest Unsorted Continuous Array

Take a look at this code,

def findUnsortedSubarray(self, nums: List[int]) -> int:

    mi , ma = -1 , -1 

    # creating a new sorted array
    lis = sorted(nums)

    # To find the start index of the subarray
    for i in range(len(nums)):
        if lis[i] != nums[i]:
            mi = i
            break

    # To find the end index of the subarray
    for i in range(len(nums)-1 ,-1,-1):
        if lis[i] != nums[i]:
            ma = i
            break

    # returns the length of the Shortest unsorted continuous subarray
    return 0 if mi ==-1 or ma == -1 else len(nums[mi:ma+1])

.
Here we initiate the variables miand mawith the value -1 because we are not going to use negative indexes, so it will remain unchanged if the array is sorted.

In the first for loop, we traverse from the start to the end and if we find a mismatch i.e. the unsorted element, we break the loop. And similarly the second for loop does the same from the end to the start.

And finally, we return the length of the shortest unsorted continuous subarray.

If we look at the runtime and memory of this solution, we see that this solution is even faster because in the best case it does not need to traverse through the whole array.

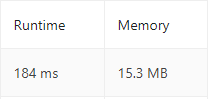
The Time Complexity & Space Complexity of this solution is O(n), where n is the size of the array.

Conclusion

As said before, a problem can be solved in multiple number of ways. There is no right method or wrong method. But always try to go with the one that saves you time and space.

With this article at OpenGenus, you must have the complete idea of Shortest Unsorted Continuous Subarray.