Syntax Analysis in Compiler Design

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

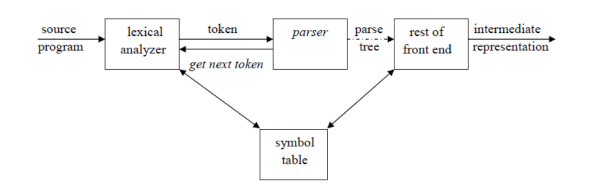
In this article, we discuss the second phase in compiler design where written code is evaluated for correctness.

Table of contents:

Definitions
The parser
Context free grammars (CFGs)
Derivations
Parse Tree
Ambiguity
Left recursion
Left factoring
Top down parsing
- Recursive descent
- Predictive Parser
Parsing table construction
LL(1) Grammar
Bottom-up parsing
Operator precedence parsing

Pre-requisites:

Definitions

Parse tree/syntax tree - This is a hierarchical representation of terminals and non-terminals.
Syntax error - This is an incorrect construction of source code.
Sentinel - Given a grammar G with start symbol S, if S -> alpha, where alpha may contain terminals or non-terminals, Alpha is referred to as the sentinel form of G.
Yield/Frontier of a tree - This is the sentinel form in the parse tree..
A parser is a program that takes in an input string and produces a parse tree if the input string is valid or an error message indicating that the input string is invalid.
A derivation is a sequence of production rules useful to get the input string.

This phase will it determine whether the input given is correctly written in the programming language used to write it.
A derivation process will try to produce the input string, if the input can be reproduced then it is valid otherwise an error(syntax error) is reported back to the syntax analyzer.

Actions during this phase.

Reporting of syntax errors.
Evaluating correctness of expressions.
Construction of a parse tree.
Obtaining of tokens from the previous phase(lexical analysis) as its input.

The parser

The parser determines syntactic validity of an input and builds a tree which is used by subsequent phases of the compiler.

syntax1

Parsers can either be;
Top Down where parse trees are built from root(top) to leaves(bottom) or Bottom Up where parse trees are built from leaves(bottom> to root(top).

Context free grammars (CFGs)

This is a set of recursive rules used to generate patterns of a string.
They are used to describe programming languages and to generate parsers automatically in compilers.

To generate context free languages, they take a set of variables which are defined recursively by a set of production rules.

Components of context free grammars

Terminal symbols - characters that appear in the language/strings generated by a grammar, they appear on the right side always.
Non-terminal symbols - placeholders for patterns of terminal symbols that can be generated by non-terminal symbols. They always appear on the left side by can also appear on the right side. Strings produced by a CFG contains symbols from a set of non-terminals.
Production rules - These are rules for replacing non-terminal symbols, eg; variable -> string of variables and terminals;
Start symbol - a non-terminal that appears in the initial string generated by the grammar.

CFG is described by a four-element tuple, (V, Σ , R, S) where;
V is a finite set of non-terminal variables
Σ is a finite set of terminal symbols disjoint from V
R is a set of production rules where each production rule maps a string s∈(V∪Σ)∗.
S which is a start symbol.

L(G) is the language generated by G which is a set of sentences.
A sentence L(G) is a string of terminal symbols of G.
If S is the start symbol of G then w is a sentence of L(G) iff s => w, where w is a string of terminals of G.
If G is a context free grammar then L(G) is a context free language.
Two grammars G1 and G2 are equivalent if they produce the same grammar.
Given a production S => a
If α contains non-terminals it is referred to as a sentential form of G, otherwise it is called a sentence of G.

Derivations

During parsing of a sequential form of input, the parser decides the non-terminal to be replaced and the production rule by which the non-terminal will be replaced .
Left-most and right-most derivations are used to decide the non-terminal to be replaced with production rule.

Left-most derivation.
The input is scanned and replaced from left to right. A left-sentential form is derived from this derivation.

Right-most derivation.
The input is scanned and replaced from right to left. A right-sentential form is derived from this derivation.

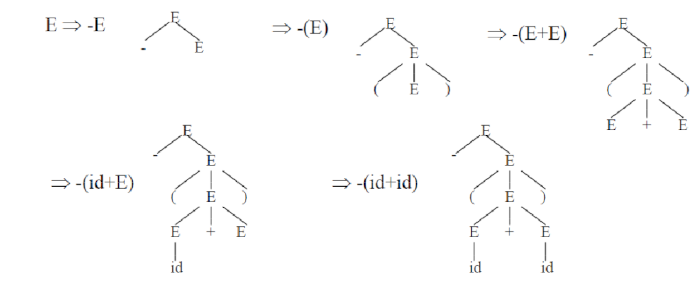
An example.
Given the grammar
G : E → E+E | E $*$ E | ( E ) | - E | id
We are to derive –(id+id)

Left-Most Derivation.


E	-E
E	-(E)
E	(E+E)
E	(id+E)
E	(id+id)

Right-Most Derivation.


E	-E
E	-(E)
E	(E+E)
E	(E+id)
E	(id+id)

Parse Tree

This is a graphical depiction of a derivation.
In a parse tree;

The inner nodes are non-terminal symbols
The leaves of a parse tree are terminal symbols
The inorder-traversal of the tree will give the original input string

Examples of Parse Trees.

syntax2

Ambiguity

A grammar that produces more than one parse for a sentence is said to be ambiguous grammar.

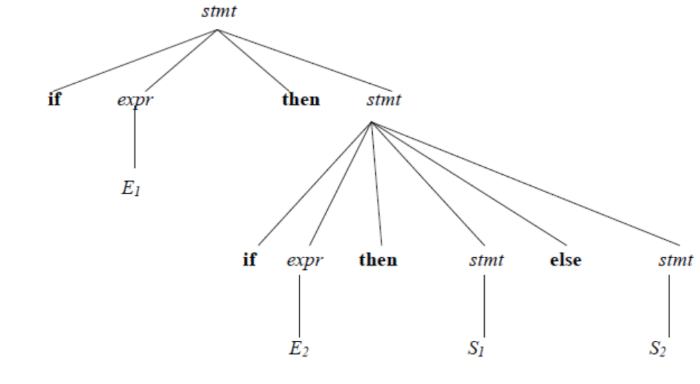
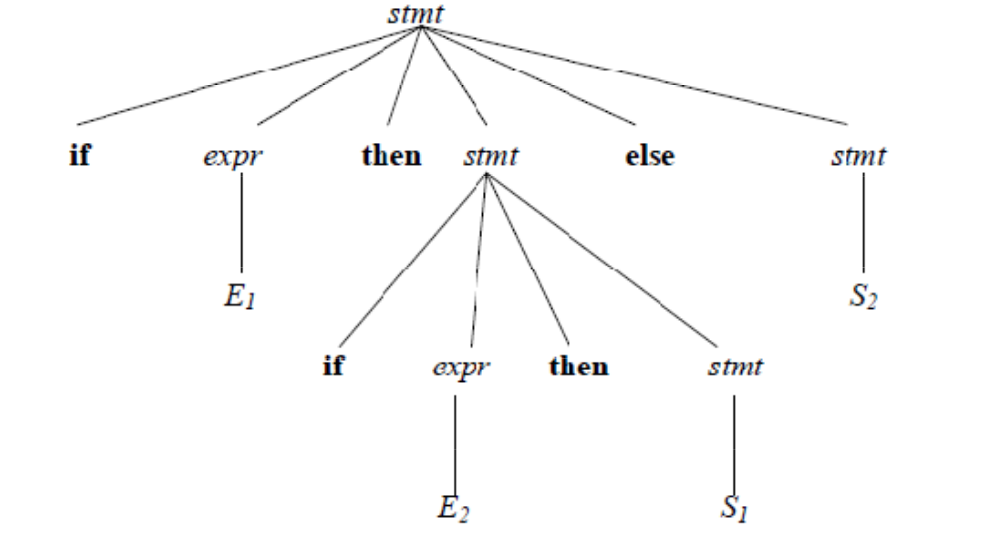
An example.
Given the ambiguous grammar G: stmt →if expr then stmt | if expr then stmt else stmt | other
Using the string if E1 then if E2 then S1 else S2
We have the following parse trees for the left-most derivation

Tree 1
syntax3

Tree 2
syntax4

To eliminate ambiguity we use the following grammar;
stmt →matched_stmt | unmatched_stmt
matched_stmt → if expr then matched_stmt else matched_stmt | other *
unmatched_stmt → if expr then stmt | if expr then matched_stmt else unmatched_stmt

Left recursion

A grammar with a non-terminal A such that there exists a derivation
A => Aα for some string α is said to be left recursive.

Elimination left recusion.
If there is a production A → Aα | β, replace it with a sequence of two productions A → βA’ and A’ → αA’ | ε without changing the set of strings derivable from A.

An example.
We have the following grammar for arithmetic expressions;
E → E+T | T
T → T $*$ F | F
F → (E) | id

We eliminate left recursion for E as follows;
E → TE’
E’ → +TE’ | ε

We eliminate left recursion for T as follows;
T → FT’
T’→ $*$ FT’ | ε

The obtained grammar after left recursion is;
E → TE’
E’ → +TE’ | ε
T → FT’
T’ → $*$ FT’ | ε
F → (E) | id

Left factoring

This is removing common left factors that appear in two productions of the same non-terminal to avoid back-tracking by the parser.
Grammar produced is suitable for predictive parsing.
When it is not clear which alternative productions to use to expand a non terminal A, we rewrite the A-productions to defer the decision until enough of the input has been seen to make the right decision.

Consider the grammar;
S→ iEtS | iEtSeS | a
E →b

The left-factored grammar is;
S → iEtSS’ | a
S’ → eS | ε
E → b

Top down parsing

Here we try to get the left-most derivation for an input string.
It is categorized into;

1. Recursive descent.

Recursive descent parsers associate each non-terminal with a procedure whose goal is to read a sequence of input characters generated by the corresponding non-terminal and return a pointer to the root of the parse tree for the non-terminal.
To match a terminal symbol, the input is compared to the non-terminal symbol and if they agree the procedure is successful.
To match a non-terminal symbol, the procedure calls the corresponding procedure for the non-terminal, hence the name recursive.

An example.
Given the grammar,
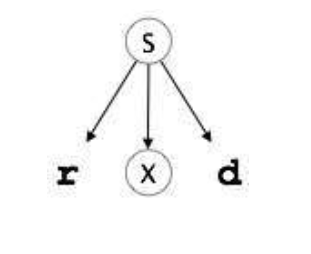
S → rXd | rZd
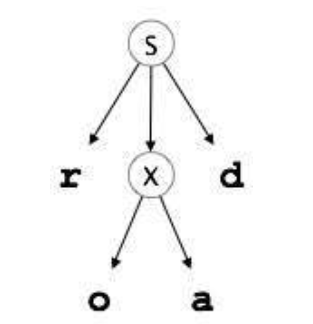
X → oa | ea
Z → ai

and an input string read.

The top-down parser will construct a parse tree in the following steps.

It starts with S from the production rules and matches its yield to the left-most letter of the input string 'r'.

syntax5

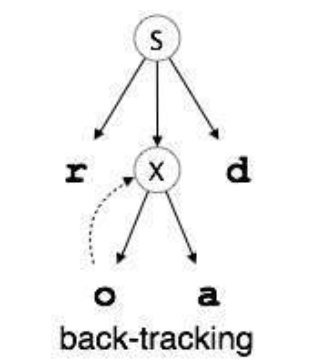
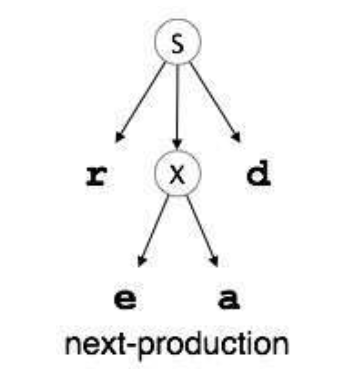
The parser advances to the next input letter in the input string 'e'. It expands the non-terminal 'X' and chaeck for its production from the left (X -> oa) and since it desnot match, the parser backtracks to obtain the next production of X, (X -> ed)

syntax6

syntax7

After the matching is complete, the input string is accepted.

syntax8

2. Predictive Parser.

This is a special case of recursive descent parsing where no back-tracking is required.
This is achieved by eliminating left recursion and performing left factoring which will remove the need for backtracking in most cases.
Look ahead pointer is also used to point to the next input symbols.
It faces the problem of trying to determine the production to be applied for a non-terminal in case of multiple alternatives.

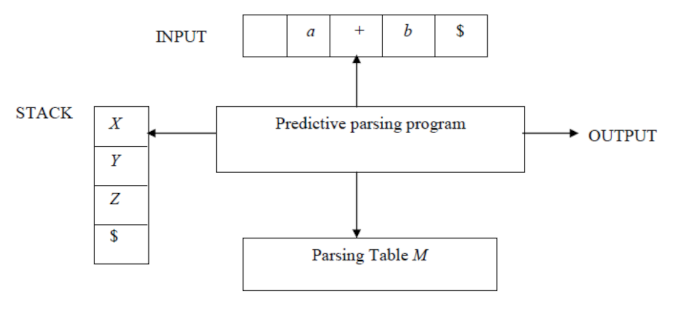
syntax9

The input buffer consists of strings that are to be parsed, The $ is used to denote that the input is consumed.
Stack data structure will contain a sequence of grammar symbols. The $ is used to denote the bottom of the stack.
The parsing table is a 2D array T[A, a] where 'A' is a non-terminal and 'a' is a terminal. It is used as a reference by the parser for making decisions on the input and stack element combination.
The stack and table are used to generate the parse tree.

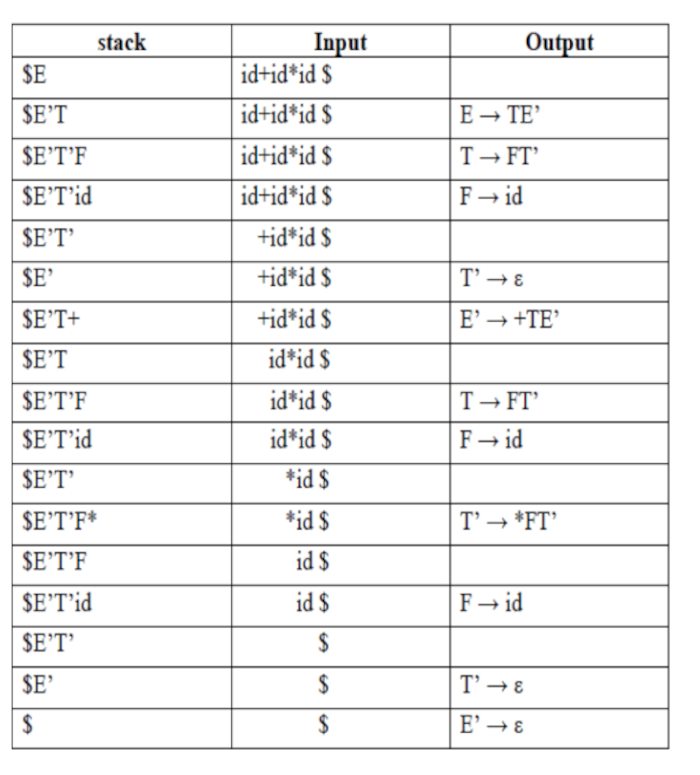
An Example.
Given a string w and a parsing table M for a grammar G.

The parser will initially have $S on the stack with S, the start symbol of G on top and w$ in the input buffer.
A parse for the input is produced as follows;

set ip to point to the first symbol of w$.

repeat
let X be the top stack symbol, a is symbol pointed to by ip
if X is terminal or $ then
    if X = a then
        pop X from stack and advance ip
    else
        error()
else
    if T[X, a] = X -> Y1Y2,...,Yk begin
        pop X from stack
        push Yk, Yk-1,...,Y1 to stack
        output the production X -> Y1, Y2,...,Yk
    end
    else error()
until X = $

The output is a left-most derivation of w, otherwise an error is produced.

Parsing table construction

The construction of a parsing table is aided by two functions associated with a grammar G.
These are the first and follow sets.

The FIRST set.

The first set is created to know the terminal symbol derived in the first position by a non-terminal.

Rules for first set are,

If X is terminal, then FIRST(X) is {X}
If X -> ε is a production, add ε to FIRST(X)
if X is non-terminal and X -> aα is a production add a to FIRST(X)
If X is non-terminal and X -> Y1, Y2,...,Yk is a production, place a in FIRST(X) if for some i, a is in FIRST(Yi) and ε is in all of FIRST(Y),...FIRST(Yi-1).
that is, Y1,...,Yi-1 => if ε is in FIRST(Yj) for all j = 1, 2, 3,...,k then add ε to FIRST(X).

The FOLLOW Set.

FOLLOW(A), for a non-terminal A is the set if terminals a that can appear immediately to the right of A in a sentinel form.
That is, the set of terminals a such that there exists a derivation of the form S =>xαAaβ for some α and β

Rules for follow set are,

If S is a start symbol, FOLLOW(S) contains $.
If there is a production a -> αBβ, everything in the FIRST(β) except ε is placed in FOLLOW(B).
If there is a production A -> αB or a production A -> αBβ wherer FIRST(β) contains ε, everything in FOLLOW(A) is in FOLLOW(B).

An example.
Consider the grammar.
E → E+T | T
T→ T $*$ F | F
F → (E) | id

Eliminate left recursion.
E → TE’
E’ → +TE’ |ε
T → FT’
T’ → $*$ FT’ | ε
F → (E) | id

The FIRST() set;
FIRST(E) = { ( , id }
FIRST(E’) ={ + ,ε }
FIRST(T) = { ( , id }
FIRST(T’) = { $*$ , ε }
FIRST(F) = { ( , id }

The FOLLOW() set;
FOLLOW(E) = { $, ) }
FOLLOW(E’) = { $, ) }
FOLLOW(T) = { +, $, ) }
FOLLOW(T’) = { +, $, ) }
FOLLOW(F) = {+, * , $ , ) }

The parsing table.

syntax10

The stack implementation.

syntax11

LL(1) Grammar

This is grammar is context-free grammar whose parsing table will not have
multiple entries.
L -> scanning input from left to right
L -> the second L is for production of the left-most derivation.
1 -> Use of only one input symbol for lookahead at each step for parsing decision making.

An example.
Consider the grammar;
E --> TE'
E' --> +TE' | ε
T --> FT'
T' --> $*$ FT' | ε
F --> id | (E)

FIRST() set.
FIRST(E) = { id, ( }
FIRST(E') = {{ +, ε }
FIRST(T) = { id, ( }
FIRST(T') = { *, ε }
FIRST(F) = { id, ( }

FOLLOW set.
FOLLOW(E) = { $, ) }
FOLLOW(E') = { $, ) }
FOLLOW(T) = { +, $, ) }
FOLLOW(T') = { +, $, ) }
FOLLOW(F) = { *, +, $, ) }

The parsing table.

Non-terminals	id	+	*	(	)	$
E	E -> TE'			E -> TE'
E'		E' -> +TE			E' -> ε	E' -> ε
T	T -> FT'			T -> FT'
T'		T' -> ε	T' -> $*$ FT'		T' -> ε	T' -> ε
F	F -> id			F -> (E)

From the table, the null productions are under the FOLLOW set of a symbol and all other productions lie under the FIRST set of the symbol.

Another Example.
Given the grammar
S --> A | a
A --> a

FIRST() set.
FIRST(S) = { a }
FIRST(A) = { a }

FOLLOW() set.
FOLLOW(S) = { $ }
FOLLOW(A) = { $ }

The parsing table.

| Non-terminals | FIRST() set | FOLLOW() set |
|---|---|
| S -> A/a | {a} | {$} |
| A -> a | {a} | {$} |

Question.

Which of the two productions is feasible for LL(1) parser?

Actions of predictive parser involve;
Shift - next input symbol is shifted to the top of the stack
Reduce - handle within the stack is replaced with a non-terminal
Accept - parsing completes successfully.
Error - a syntax error occurs and error recovery is initiated.

Bottom-up parsing

This is the construction of a parse tree for an input string starting from the leaves(bottom) to the root(top).
A shift-reduce parser is a type of a bottom up parser.

Drawbacks of shift reduce parser.

Shift-reduce conflict - This is whereby the parser cannot decide whether to shift or reduce.
Reduce-reduce conflict - Whereby the parser cannot decide which reductions to make among the several.

Operator precedence parsing

This is an efficient way of constructing a shift-reduce parser.
An Operator-grammar is a grammar used to define mathematical operators, they have the property that no production has either an empty right hand side(null productions) or two adjacent non-terminals in its right hand side.
An operator grammar is used for the construction of an operator precedence parser.

Given the grammar.
E -> EAE | (E) | -E | id
A -> + | - | * | / | ↑

The right side has three consecutive non-terminals, that is EAE, therefore the grammar is written as

E -> E + E | E - E | E * E | E / E | E ↑ E | -E | id.

Precedence relations.

a < b (a yields precedence to b).
a = b (a has same precedence tp b).
a > b (a takes precedence over b).

Advantages pf operator precedence.

Easy implementation.
The grammar can be ignored once a precedence relation has been made between all pairs of non-terminals therefore the grammar is not refered to during implementation.

Drawbacks.

Only a small class of grammar can be parsed using operator-precedence parser.
Handling tokens is hard, that is (-) has two different precedences.

LR parsers

This parsers implement an efficient bottom-up syntax analysis used to parse a large class of CFGs(LR(k)) parsing.
L -> left to right scanning
R -> construction of the right most derivation in reverse
k -> represent the number of input symbols.

Types of LR parsers.

Simple LR parser(SLR).
Canonical LR parser(CLR)
LookAhead LR parser (LALR)

Advantages.

It is efficient and there is no backtracking
Detects syntactic errors as soon as possible
Recognizes all programming language constructs for which a CFG can be written.

Drawbacks.

Involves a lot of work to construct hence a specialized tool called a LR parser generator is used.

Parser generators

This is a tool that takes grammar as input and automatically generates source code that can parse streams of characters using the grammar.
The source code is a parser that takes the sequence of characters and tries to match the sequence against grammar.
A parse tree is the output of this operation. It will show how grammar productions are expanded into a sentence that matches the characters sequence.

With this article, you must have a strong idea of Syntax Analysis in Compiler Design.

Syntax Analysis in Compiler Design

Compiler Design

Definitions

The parser

Context free grammars (CFGs)

Components of context free grammars

Derivations

Parse Tree

Ambiguity

Left recursion

Left factoring

Top down parsing

1. Recursive descent.

2. Predictive Parser.

Parsing table construction

The FIRST set.

The FOLLOW Set.

LL(1) Grammar

Question.

Bottom-up parsing

Drawbacks of shift reduce parser.

Operator precedence parsing

Precedence relations.

Advantages pf operator precedence.

Drawbacks.

LR parsers

Types of LR parsers.

Advantages.

Drawbacks.

Parser generators

Constant Folding and Constant Propagation in Compiler Design

Xavier Initialization