
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explained the concept of Xavier Initialization which is a weight initialization technique used in Neural Networks.
Table of contents:
- What is the Definition of Initialization?
- Weight Initialization Techniques
- What Are the Disadvantages of the Sigmoid Function and tanh function?
- What is Xavier Initialization?
- Xavier Initialization in TensorFlow
What is the Definition of Initialization?
The process of setting the initial values of weights for our models, neural networks, or other deep learning architecture is known as initialization.Choosing the proper initializer is critical to our model's performance and training results in a faster convergence time and a lower loss function by adjusting our initial weights.
Weight Initialization Techniques
There are 3 main weight Initialization techniques:
- Zero Initialization
- Initialization with the same Random value
- Xavier Initialization
Zero Initialization
Putting all of the weights equal to zero is one of the simplest ways to initialize them.Because neurons learn the same characteristic throughout each cycle, this type of initialization is unsuccessful.
Rather, the identical problem occurs throughout any type of constant initialization.
As a result, constant initializations aren't recommended.
Initialization with the same Random value
Random initialization adds random values other than zeros as weights to neuron routes in an attempt to address the inadequacies of Zero or Constant Initialization.
Overfitting, Vanishing Gradient Problem, and Exploding Gradient Problem may arise if the weights are assigned values at random. As a result, this strategy isn't used.
What Are the Disadvantages of the Sigmoid Function and tanh function?
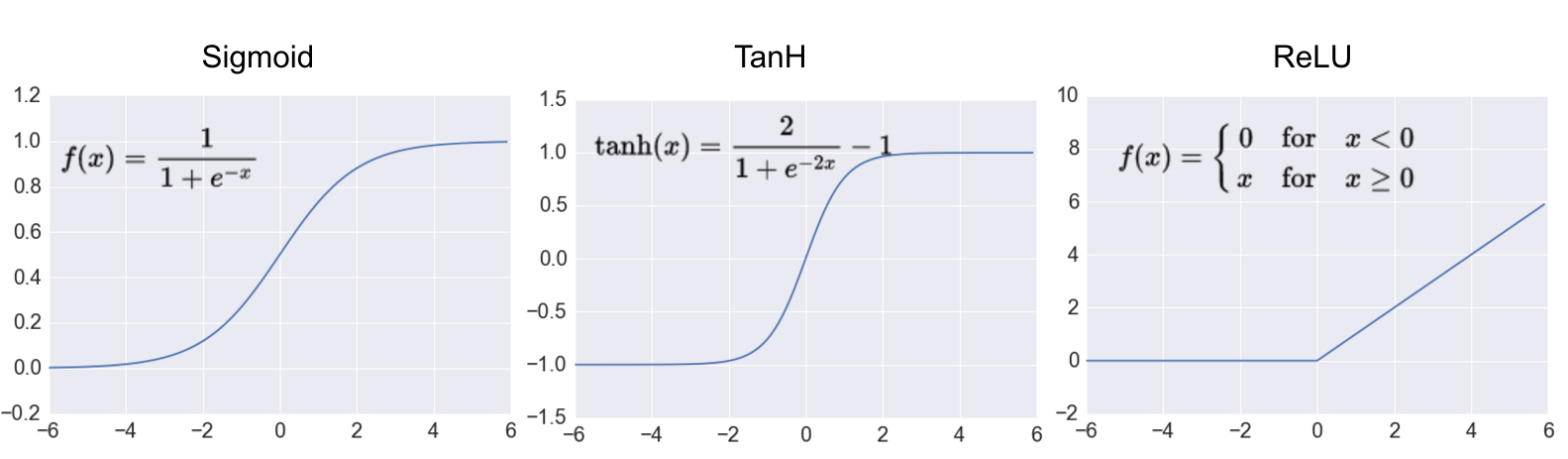
When we look at the activation functions (TanH and Sigmoid), we can see that they are mainly flat (at both ends). It only curves across a relatively tiny range of values. If you send a random input x into an activation like the Sigmoid function, the result is almost always 0 or 1. The activation function can only return a value between 0 and 1 if your x is sampled within a limited range close to 0.
Machine learning models, as you may have noticed, are extremely sensitive to weight initialization. The same neuron network trained with the same data that converges swiftly sometimes may not converge at all if the initialization is not done carefully.
And the above characteristic of activation functions is substantially to blame for this phenomenon.
Remember that an activation function's input is a weighted sum of inputs Xi.
If the weighted sum lies outside the activation function's sweet spot, the neuron's output is nearly fixed at the maximum or lowest.
The "adjust-ability" of this neuron in this case is quite bad from the standpoint of backpropagation, because the activation function is virtually flat at the input point and the gradient evaluated at that point is close to zero.
You don't know which direction to change the input if it's near to zero.
The neuron is being caught in this scenario (commonly referred to as "saturated"). Because the neuron lacks "adjust-ability," it will be difficult for it to escape the stuck condition. (ReLU is superior because it only has one flat end.) As a result, while initializing the weights of a neuron network, attention must be taken. You will most likely start with saturated neurons if the initial weights are too large or small. This will result in a sluggish or non-existent convergence.
If you want your neural network to run effectively, you must first set up the network with the appropriate weights. Before we begin training the network, we must ensure that the weights are within a reasonable range. Xavier initialization comes into play at this point.
What is Xavier Initialization?
Xavier Initialization, also known as Glorot Initialization, is a neural network initialization strategy. Weights are assigned from values of a uniform distribution in Xavier/Glorot weight initialization as follows:
- fan_in = Number of input paths towards the neuron
- fan_out = Number of output paths towards the neuron
- U is uniform distribution
- σ=√2inputs+outputs
- wi is the i-th weight
Xavier/Glorot Initialization, also known as Xavier Uniform Initialization, is appropriate for layers with Sigmoid activation functions.
The Xavier initialization keeps the variance in some limits as each layer passes, allowing us to fully utilize the activation functions.
This method can be broken down into two parts.
Uniform Xavier initialization: for x=√6inputs+outputs, draw each weight, w, from a random uniform distribution in [-x,x].
Initialize each weight, w, using a normal distribution with a mean of 0 and a standard deviation equal to σ=√2inputs+outputs
Xavier Initialization in TensorFlow
import tensorflow as tf
w2 = tf.Variable(tf.contrib.layers.xavier_initializer()(([4,4])),name="weights")
w = tf.get_variable('w', shape=[4, 4])
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
print(sess.run(w))
print(sess.run(w2))
Weight Initialization is a crucial topic in Neural Networks, and choosing the proper Initialization strategy can have a significant impact on the model's accuracy. As a result, an appropriate weight initialization technique must be adopted, taking into account numerous parameters such as the activation function used.
With this article at OpenGenus, you must have the complete idea of Xavier Initialization.

