
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 35 minutes
In this problem we are given with a string and a dictionary of words, we need to find if the string can be segmented to words so that all the segmented words are present in the dictionary.
For Example:
dictionary: {i, hello, mango, man, how, ice, cream, like, cell}
string: "icelikemango"
Output: Yes
The string can be segmented as "ice like mango".
The above problem can be solved by backtracking, taking consideration of all the possible segmentation, i.e if we need to print all those possible segmentation then we can do this with backtracking in O(n2*s) time. But if we only need to find that it is possible to segment the string in such a way or not then we can solve it efficiently with memoization and dynamic programming in O(n*s) time where s is the length of the largest string in the dictionary and n is the length of the given string.
Algorithm
We have explored two approaches:
- Brute force approach
- Dynamic Programming
1. Brute force approach
This is a simple recursive approach where we take each prefix of the string and match it with the dictionary and if it is present then we take the suffix of the string and recur the same. if the recursive call for suffix returns true then we return true, else we try for prefix of greater size. if none of the recur call of suffix returns true then we return false as the string cannot be segmented as per the words present in the dictionary.
def word_break_recursive(string, dictionary):
n = len(string)
if n == 0:
return True
for i in range(1,n + 1):
if dictionary.__contains__(string[0: i]) and word_break_recursive(string[i: n], dictionary) :
return True
return False
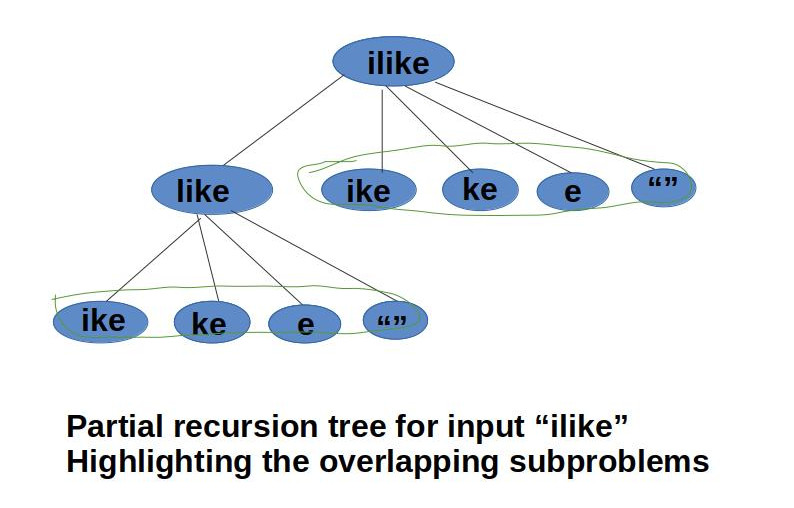
The partial recursion tree of string "ilike" is shown below, the recursive algorithm first checks for the prefix, if it is present in the dictionary, then it recurs for the suffix. If both prefix and suffix is present in dictionary, i.e both returns true then we return the function as true, else we check for different prefixes if all returns False then we return false as the output of program.
2. Dynamic Programming approach
The word break problem has overlapping subproblems and optimal substructure. In recursion we solve the overlapping subproblems multiple times. So in DP approach we memoize the olution of each subproblem so that we don't need to solve it multiple times and we can use the pre-computed results to solve the problem.
Let's understand the overlapping subproblems with a string "ilike". The partial recursion tree is shown below, in which we can see that upto depth 2 the substring "like" is already solved 2 times.
In DP approach we use a dp array of size n+1(length of string) to store the results of prefixes and apart from this we use matched_index to further optimze the complexcity. Then we will check the substrings from those indexes to the he current index. If anyone of that matches then we can divide the string up to that index and start from index next to that.
def word_break(string, dictionary):
n = len(string)
if n == 0:
return True
dp = [False for _ in range(n + 1)]
matched_index = [-1]
for i in range(n):
msize = len(matched_index)
is_matched = False
for j in range(msize - 1, -1, -1):
sub_string = string[matched_index[j] + 1: i + 1]
if dictionary.__contains__(sub_string):
is_matched = True
break
if is_matched:
dp[i] = True
matched_index.append(i)
return dp[n - 1]
The time complexity of the algorithm is O(n * s) where s is the length of the largest string in the dictionary and n is the length of the given string.
As we run the loop only once, which takes O(n) time and each time we match it with the dictionary word which can have a length <=s so overall time taken by the program is O(n * s).
Implementation
Code in python3
def word_break(string, dictionary):
n = len(string)
if n == 0:
return True
dp = [False for _ in range(n + 1)]
matched_index = [-1]
for i in range(n):
msize = len(matched_index)
is_matched = False
for j in range(msize - 1, -1, -1):
sub_string = string[matched_index[j] + 1: i + 1]
if dictionary.__contains__(sub_string):
is_matched = True
break
if is_matched:
dp[i] = True
matched_index.append(i)
return dp[n - 1]
dictionary = ["hello", "man", "mango", "icecream", "and", "go", "i", "like", "ice", "cream", "cell"]
# print 'Yes' if the dictionary conatins the segmented words else print 'No'
print("Yes" if word_break("ilike", dictionary) else "No")
Output
"Yes"
Recursive Approach Implementation in python3
def word_break_recursive(string, dictionary):
n = len(string)
if n == 0:
return True
for i in range(1,n + 1):
if dictionary.__contains__(string[0: i]) and word_break_recursive(string[i: n], dictionary) :
return True
return False
dictionary = ["mobile", "samsung", "sam", "sung", "man", "mango", "icecream", "and", "go", "i", "like", "ice", "cream"]
print("Yes" if word_break_recursive("ilike", dictionary) else "No")
Output
Yes
Complexity
Time complexity
- Time Complexity of word break program in dp approach is O(n * s).
- Time complexity of word break program in recursive approach is O(2n*s).
Space complexity
- The word break problem takes O(n) auxiliary space.
