
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 10 minutes
The N-Queens problem is a puzzle of placing exactly N queens on an NxN chessboard, such that no two queens can attack each other in that configuration. Thus, no two queens can lie in the same row,column or diagnol.
We have already discussed the backtracking solution to the 8 Queen problem here. In the backtracking algorithm, we consider possible configurations one by one and backtrack if we hit a dead end.
The branch and bound solution is somehow different, it generates a partial solution until it figures that there's no point going deeper as we would ultimately lead to a dead end.
In the backtracking approach, we maintain an 8x8 binary matrix for keeping track of safe cells (by eliminating the unsafe cells, those that are likely to be attacked) and update it each time we place a new queen. However, it required O(n^2) time to check safe cell and update the queen.
In the 8 queens problem, we ensure the following:
- no two queens share a row
- no two queens share a column
- no two queens share the same left diagnol
- no two queens share the same right diagnol
we already ensure that the queens do not share the same column by the way we fill out our auxiliary matrix (column by column). Hence, only the left out 3 conditions are left out to be satisfied.
Applying the branch and bound approach :
The branch and bound approach suggets that we create a partial solution and use it to ascertain whether we need to continue in a particular direction or not. For this problem, we create 3 arrays to check for conditions 1,3 and 4. The boolean arrays tell which rows and diagnols are already occupied. To achieve this, we need a numbering system to specify which queen is placed.
The indexes on these arrays would help us know which queen we are analysing.
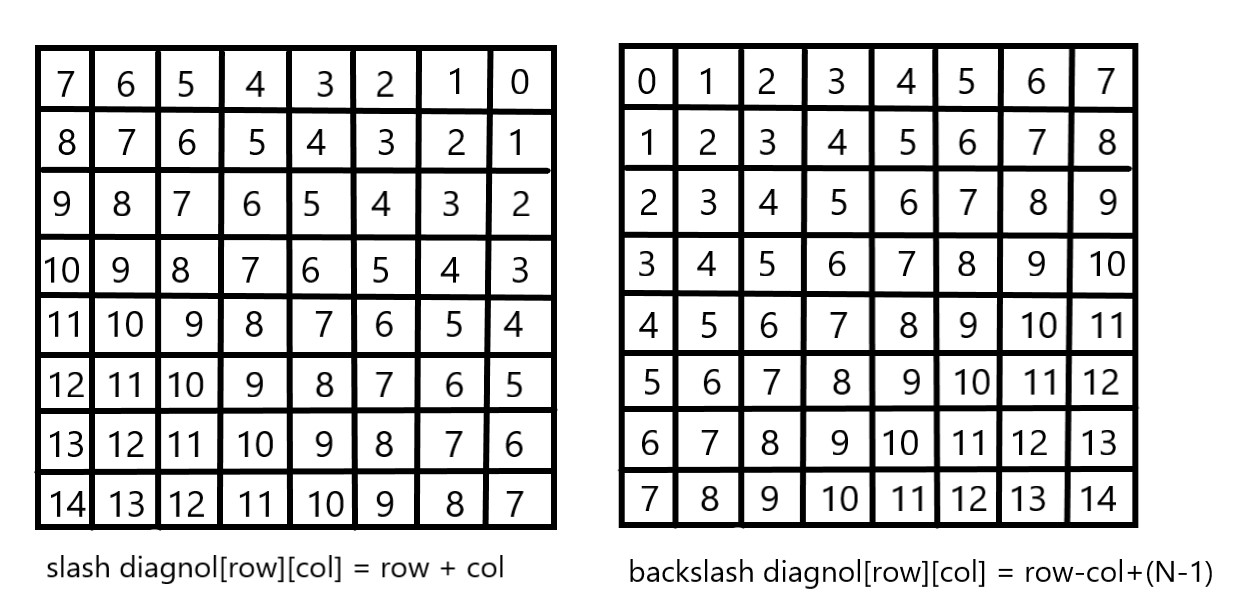
Preprocessing - create two NxN matrices, one for top-left to bottom-right diagnol, and other for top-right to bottom-left diagnol. We need to fill these in such a way that two queens sharing same top-left_bottom-right diagnol will have same value in slashDiagonal and two queens sharing same top-right_bottom-left diagnol will have same value in backSlashDiagnol.
slashDiagnol(row)(col) = row + col
backSlashDiagnol(row)(col) = row - col + (N-1) { N = 8 }
{ we added (N-1) as we do not need negative values in backSlashDiagnol }
For placing a queen i on row j, check the following :
- whether row 'j' is used or not
- whether slashDiagnol 'i+j' is used or not
- whether backSlashDiagnol 'i-j+7' is used or not
If the answer to any one of the following is true, we try another location for queen i on row j, mark the row and diagnols; and recur for queen i+1.
Implementation
#include<bits/stdc++.h>
using namespace std;
int board[8][8]
int n
// function to print solution
void printSolution(int board[n][n])
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{ cout<<board[i][j]<<" ";
}
cout<<endl;
}
}
//function to check if queen can
// be placed on board[row][col]
bool isPossible(int row, int col, int slashDiagnol[n][n],
int backSlashDiagnol[n][n], bool rowLook[n],
bool slashDiagnolLook[], bool backSlashDiagnolLook[])
{
if (slashDiagnolLook(slashDiagnol[row][col] || backSlashDiagnol[row][col]
|| rowLook[row] )
return false;
return true;
}
//A recursive utility function to solve N Queen problem
bool solveNQueensUtil(int board[n][n], int col,
int slashDiagnol[n][n],int backSlashDiagnol[n][n],
bool rowLook[n], bool slashDiagnolLook[],
bool backSlashDiagnolLook[] )
{
//base case: If all queens are placed
if (col >= N)
return true;
//Consider this column and try placing
// queen in all rows one by one
for (int i = 0; i < n; i++)
{
if ( isPossible(i, col, slashDiagnol, backSlashDiagnol,
rowLook, slashDiagnolLook,
backSlashDiagnolLook) )
{
board[i][col] = 1;
rowLookup[i] = true;
slashDiagnolLook[slashDiagnol[i][col]] = true;
backSlashDiagnolLook[backSlashDiagnol[i][col] = true;
//recur to place rest of the queens
if ( solveNQueensUtil(board, col + 1, slashCode, backslashCode,
rowLookup, slashCodeLookup, backslashCodeLookup) )
return true;
// placing queen in board[i][col]
// dosen't yield a solution, backtrack
board[i][col] = 0;
rowLook[i] = false;
slashDiagolLook[slashDiagnol[i][col]] = false;
backSlashDiagnolLook[backSlashDiagnol[i][col]] = false;
}
}
//If queen can not be place in any row in
//this colum col then return false
return false;
}
/* This function solves the N Queen problem using
Branch and Bound. It mainly uses solveNQueensUtil() to
solve the problem. It returns false if queens
cannot be placed, otherwise return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
bool solveNQueens(n)
{
memset(board, 0, sizeof(board));
// helper matrices
int slashDiagnol[n][n];
int backSlashDiagnol[n][n];
// arrays to tell us which rows are occupied
bool rowLook[n] = {false};
//keep two arrays to tell us which diagonals are occupied
bool slashDiagnolLook[2*n-1] = {false};
bool backSlashDiagnolLook[2*n-1] = {false};
// initialize helper matrices
for (int r = 0; r < n; r++)
for (int c = 0; c < n; c++)
{
slashDiagnol[r][c] = r+c;
backSlashDiagnol[r][c] = (r+c-7);
}
if (solveNQueensUtil(board, 0, slashDiagnol, backSlashDiagnol,
rowLook, slashDiagnolLook, backSlashDiagnolLook) == false)
{
cout<<"No solution"<<endl;
return false;
}
// solution found
printSolution(board);
return true;
}
// main function
int main()
{
cin>>n; // can take any size from 0 to 8
solveNQueens(n);
return 0;
}
Output-
for (n = 8)
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
Breaking down lines of Code
'void printSolution(board)' -> this function prints the solution matrix (composed of 0s and 1s)
'bool isPossible(row,col,slashDiagnol,backSlashDiagnol,rowLook,slashDiagnolLook,backSlashDiagnolLook)'
-> this function makes use of the 'OR' operator to check whether any of the 3
arrays hold the value true for the same queen or not.
If they do, we need to select any other position else we continue with
the position we selected first.
'bool solveNQueensUtil(board,col,slashDiagnol,backSlashDiagnol,rowLook,slashDiagnolLook
,backSlashDiagnolLook)' -> this is a recursive function
that checks the 3 arrays for rows and diagnols to
determine the appropriate position for placing a queen.
If any of the arrays *rowLook, slashDiagnolLook or backSlashDiagnol*
holds the value true for a particular queen,
we need to search for some other location.
This is due to our algorithmic design, if we consider the chessboard
configuration in our minds and take the arrays parallel to it,
if for a particular index, we have the same truth value
in 2 or more arrays, that would imply overlap in position of different
queens; which is undesirable.
Finally, we recur the function for subsequent columns.
'bool solveNQueens(n)' -> this function simply initializes the board matrix,
the pre-processing matrices, and the row and diagnol arrays.
Consequently, it calls the utility function to solve the N-Queens problem.
'int main()' -> driver program to test above functions.
Explanation
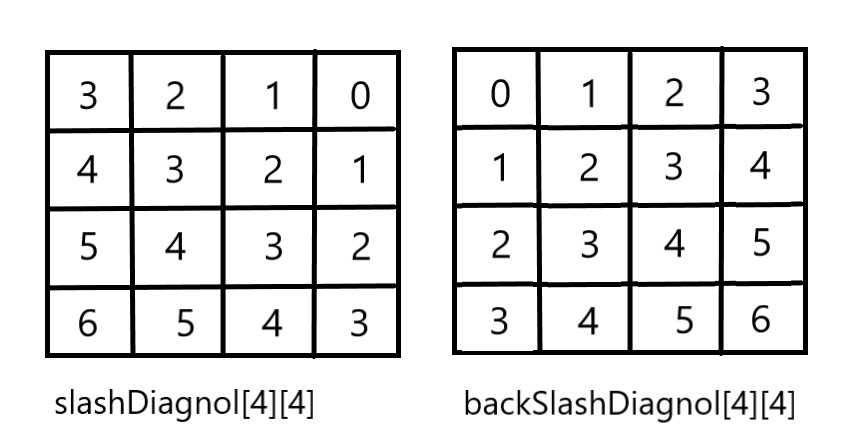
consider the example of a 4x4 chessboard
initially, board matrix:
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
rowLook array:
[ false, false, false, false]
slashDiagnolLook array (size = 2xn-1 = 7):
[ false, false, false, false, false, false, false]
backSlashDiagnolLook array (size = 2xn-1 = 7):
[ false, false, false, false, false, false, false]
preprocessed matrices are as follows:
solveNQueensUtil(arguments){
col < n : 0 < 4
for(i = 0; i<4; i++){
isPossible() = true
{
board[0][0] = 1
rowLook[0] = true
slashDiagnol[3] = true
backSlashDiagnol[0] = true
recur for (col+1) : col = 1
solveNQueensUtil(){
isPossible() = false
}
backtrack:
board[0][0] = 0
rowLook[0] = false
slashDiagnol[3] = false
backSlashDiagnol[0] = false
}
i = 1
// same layout
// for i = 1, col = 0; we obtain solution
// for i = 2, col = 0; we obtain another solution
}
Output-
0 1 0 0 0 0 1 0
0 0 0 1 1 0 0 0
1 0 0 0 0 0 0 1
0 0 1 0 0 1 0 0
Time Complexity
It has the same time complexity O(N!) as that of the backtracking algorithm, though it's performance is much better due to partial solution creation.
Question-
Solve the 0/1 Knapsack problem using branch and bound algorithm. First implement it using backtracking, then optimise it with branch and bound.
0/1 Knapsack = Given weights and profits associated with n different values respectively. Put these items in a knapsack of weight W to obtain the maximum profit. You cannot break an item, either put it whole or do not put the item in the knapsack.
