Reading time: 35 minutes

In this article, we will go through a simple yet elegant algorithm to find a clique of a given size. Clique is an interesting topic in itself given that the clique decision problem is NP-Complete and clique arises in almost all real-life applications involving graphs. Before we go into the wonderful algorithm, we will go through some basic ideas.

A clique is a subset of vertices of an undirected graph G such that every two distinct vertices in the clique are adjacent; that is, its induced subgraph is complete. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs. So we can say that a clique in an undirected graph is a subgraph that is complete.

A maximal clique is a clique that cannot be extended by including one more adjacent vertex, that is, a clique which does not exist exclusively within the vertex set of a larger clique. Maximal cliques can be very small. A graph may contain a non-maximal clique with many vertices and a separate clique of size 2 which is maximal. While a maximum (i.e., largest) clique is necessarily maximal, the converse does not hold.

A clique of size k in a graph G is a clique of graph G containing k vertices, i.e. the degree of each vertex is k-1 in that clique.
So particularly, if there is a subset of k vertices that are connected to each other in the graph G, we say that graph contains a k-clique.
A k-clique can be a maximal clique or can be a subset of a maximal clique, so if a graph contains a clique of size more than k then it definitely contains a clique of size k.
For example the graph shown below:

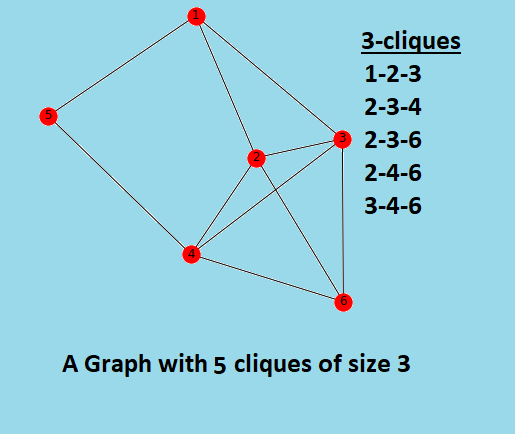
Algorithm

We can find all the 2-cliques by simply enumerating all the edges.

To find k+1-cliques, we can use the previous results. Compare all the pairs of k-cliques. If the two subgraphs have k-1 vertices in common and graph contains the missing edge, we can form a k+1-clique.

def k_cliques(graph):
    # 2-cliques
    cliques = [{i, j} for i, j in graph.edges() if i != j]
    k = 2

    while cliques:
        # result
        yield k, cliques

        # merge k-cliques into (k+1)-cliques
        cliques_1 = set()
        for u, v in combinations(cliques, 2):
            w = u ^ v
            if len(w) == 2 and graph.has_edge(*w):
                cliques_1.add(tuple(u | w))

        # remove duplicates
        cliques = list(map(set, cliques_1))
        k += 1

The above algorithm of finding k-clique in a graph G takes polinomial time for its execution. The algorithm starts from 2-clique pairs and use this as base data to find 3-cliques and more.

To generate 3-cliques from 2-cliques we take each combination pair of 2-cliques and take intersection of the pair, if the intersection is an edge and it is present in the graph then the union of the pair is a clique of size 3. By doing intersection of the pair we find the missing edge so that the 2-clique can be extended to 3-clique, and if the edge is present in the graph then we extend the 2-clique pair into 3-clique and store it. In similar way we generate k+1-clique from k-clique.

Let's understand with it with a graph with 4 vertices:

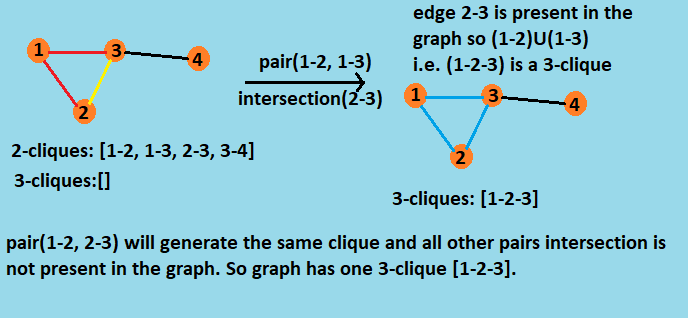
To find k-cliques we iterate the same method O(k) times. The method which finds the p+1-clique from p-clique takes O(n) time where n is number of vertices. So in overall the algorithm takes O(n^k) time in the worst case.

Implementation

Code in Python3

from itertools import combinations
import networkx as nx


def k_cliques(graph):
    # 2-cliques
    cliques = [{i, j} for i, j in graph.edges() if i != j]
    k = 2

    while cliques:
        # result
        yield k, cliques

        # merge k-cliques into (k+1)-cliques
        cliques_1 = set()
        for u, v in combinations(cliques, 2):
            w = u ^ v
            if len(w) == 2 and graph.has_edge(*w):
                cliques_1.add(tuple(u | w))

        # remove duplicates
        cliques = list(map(set, cliques_1))
        k += 1


def print_cliques(graph, size_k):
    for k, cliques in k_cliques(graph):
        if k == size_k:
            print('%d-cliques = %d, %s.' % (k, len(cliques), cliques))


nodes, edges = 6, 10
size_k = 3
graph = nx.Graph()
graph.add_nodes_from(range(nodes))
graph.add_edge(1, 2)
graph.add_edge(1, 3)
graph.add_edge(1, 5)
graph.add_edge(2, 3)
graph.add_edge(2, 4)
graph.add_edge(2, 6)
graph.add_edge(3, 4)
graph.add_edge(3, 6)
graph.add_edge(4, 5)
graph.add_edge(4, 6)

print_cliques(graph, size_k)

Output

3-cliques = 5, [{3, 4, 6}, {2, 3, 6}, {2, 4, 6}, {1, 2, 3}, {2, 3, 4}].

Complexity

Time Complexity

• The k-clique algorithm takes O(n^k) (i.e. polynomial) time in the worst case.

Space Complexity

• The k-clique algoorithm takes O(n²) auxiliary space in the worst case.

Related articles

References

• Publication of K-clique on springer.com
• discussion page on K-clique on cs.stackexchange