Augmented Data Structures

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Augmenting a data structure (or Augmented Data Structure) means using a existing data structure and making some changes in that data structure to fit our needs. This helps us take advantage of stock data structure that almost, but not quite, solves our problem, and add some finishing touches that makes it solve our problem.

for example -

let take the example of a binary tree , In the binary tree if we define a binary tree in such a way that for any node in the tree it's left subtree will have all the node values smaller then the current node and all the nodes in the right subtree will have node values greater then the current node then in this case we have created a binary search tree and we can search any element in the tree in O(logn) time and this is the basic idea of augmenting data structure in which we change an existing data strucuture and change it's properties and structure a little to solve our problem.

iq10

More examples based on augmenting the data structure

There are numerous examples of augmenting data structures and augmenting is all about making changes in the existing data structure to solve our problem.

1.let's take a hash map and add a pointer to each element, which points to yet another element of the hash map. It effectively creates a singly linked list on top of the hash map. This data structure is often used to implement the LRU cache eviction algorithm.

let's take a binary search tree and add add some sort of topology information to each node, so that you can keep the tree depth close to log n, where n is the size of the tree. You end up with a self-balancing binary search tree.
let's take a singly linked list, and add an additional node in one direction. name the existing node left and the new node right. You also call the current node the parent of left and right. You end up with a binary tree

Effect on time complexity on augmenting the data structure

We must ensure that after augmenting the data structure the time complexity of the data structure with respect to other operations should not change a lot , let's say

we have a data structure ( say D ) having Time complexity before augmenting as

search - O(n)
insert - (logn)
delete - (logn)

and after augmenting the D the time complexities are changed to

search - O(logn)
insert -O(n)
delete - O(n)

and let's say that in this data structure there are very frequent inserts and deletes and very few searches then augmenting this way would result in slower overall performance and instead of increasing the performance we have degraded the performance of D .

So we should always keep in mind the effects of augmenting the data structure and we should only augment the data structure if it would result in overall better performance of the data structure.

In the above example let's say after augmenting D complexities are changed to -

search - O(logn)
insert - O(logn)
delete - O(logn)

Then this would serve the true purpose of augmenting D as the overall performance of the data strucure has improved.

Things to keep in mind before augmenting

Simply imposing new conditions and adding new constraints is not enough we must ensure that after adding , deleting and updating new element the data strucure must retain it's properties that's why you must have good understanding of the data structure before trying to augment it.

Algorithm for augmenting data structures

Choose underlying data structure on which you want to add additional information to make new data structure.
Add additional information on the selected data structure.
Verify that information can be maintained for modifying operations.
(Insertion,Deletion,etc)

4.add new operations to our data strucure according to our needs and that can be performed on the data structure.

let's solve a problem using augmentation of data structure

Problem

Given a binary search tree and a integer k our task is to find out sum of all the elements which is less or equal to the k th smallest element in binary search tree

Naive approach

we can solve this problem by maintaining a x variable which keeps the count of visited nodes and a sum variable both initialzed to zero then we can do a inorder traversal of the binary tree and keep summing the value of node until the count of visited node is not equal to k , when visited nodes reaches the value k we can simply return the value of sum.

for detailed explanation you can refer to this article -https://iq.opengenus.org/sum-of-k-smallest-elements-in-binary-search-tree/

Augmenting

The complexity of solving the problem using the above method is O(n) where n is the no. of the nodes in the binary tree.

we can also solve this problem with much better O(h) time complexity
(here h is the height of the binary search tree)

here augmentation of the binary search tree comes in picture , we will use the existing binary search tree and do some structural changes to our data structure to reduce the time complexity of finding the answer.

Structure of Augmented Tree

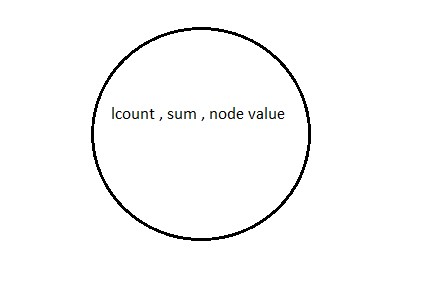
Binary Search Tree Node contain to extra fields : lCount , Sum

For each Node of Binary Search Tree
lCount : store how many left child it has
Sum : store sum of all left child it has
node value : store value at the current node

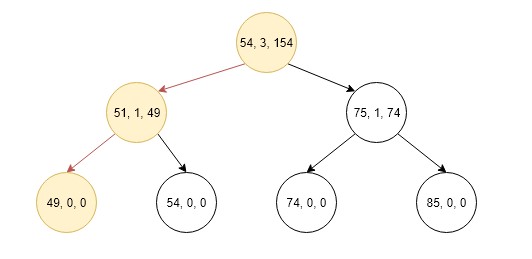
consider the following augmented binary search tree

for detailed explanation on how insertions work in this augmented binary search tree and how this binary tree is created with code explanation you can refer to the following article-

https://iq.opengenus.org/sum-of-k-smallest-elements-in-binary-search-tree/

Algorithm for finding sum of k smallest elements in Binary Search Tree

Find Kth smallest element
[ temp_sum store sum of all element less than equal to K ]

ksmallestElementSumRec(root, K, temp_sum)

  IF root -> lCount == K + 1
      temp_sum += root->data + root->sum;
      break;
  ELSE
     IF k > root->lCount   // Goto right sub-tree
        temp_sum += root->data + root-> sum;
        ksmallestElementSumRec(root->right, K-root->lcount+1, temp_sum)
     ELSE
        // Goto left sun-tree
        ksmallestElementSumRec( root->left, K, temp_sum)

Implementation of above algorithm is given below.

// C++ program to find Sum Of All Elements smaller 
// than or equal t Kth Smallest Element In BST 
#include <bits/stdc++.h> 
using namespace std; 

/* Binary tree Node */
struct Node 
{ 
	int data; 
	int lCount; 
	int Sum ; 
	Node* left; 
	Node* right; 
}; 

//utility function new Node of BST 
struct Node *createNode(int data) 
{ 
	Node * new_Node = new Node; 
	new_Node->left = NULL; 
	new_Node->right = NULL; 
	new_Node->data = data; 
	new_Node->lCount = 0 ; 
	new_Node->Sum = 0; 
	return new_Node; 
} 

// A utility function to insert a new Node with 
// given key in BST and also maintain lcount ,Sum 
struct Node * insert(Node *root, int key) 
{ 
	// If the tree is empty, return a new Node 
	if (root == NULL) 
		return createNode(key); 

	// Otherwise, recur down the tree 
	if (root->data > key) 
	{ 
		// increment lCount of current Node 
		root->lCount++; 

		// increment current Node sum by adding 
		// key into it 
		root->Sum += key; 

		root->left= insert(root->left , key); 
	} 
	else if (root->data < key ) 
		root->right= insert (root->right , key ); 

	// return the (unchanged) Node pointer 
	return root; 
} 

// function return sum of all element smaller than and equal 
// to Kth smallest element 
void ksmallestElementSumRec(Node *root, int k , int &temp_sum) 
{ 
	if (root == NULL) 
		return ; 

	// if we fount k smallest element then break the function 
	if ((root->lCount + 1) == k) 
	{ 
		temp_sum += root->data + root->Sum ; 
		return ; 
	} 

	else if (k > root->lCount) 
	{ 
		// store sum of all element smaller than current root ; 
		temp_sum += root->data + root->Sum; 

		// decremented k and call right sub-tree 
		k = k -( root->lCount + 1); 
		ksmallestElementSumRec(root->right , k , temp_sum); 
	} 
	else // call left sub-tree 
		ksmallestElementSumRec(root->left , k , temp_sum ); 
} 

// Wrapper over ksmallestElementSumRec() 
int ksmallestElementSum(struct Node *root, int k) 
{ 
	int sum = 0; 
	ksmallestElementSumRec(root, k, sum); 
	return sum; 
} 

/* Driver program to test above functions */
int main() 
{ 
    Node *root = NULL; 
	root = insert(root, 20); 
	root = insert(root, 8); 
	root = insert(root, 4); 
	root = insert(root, 12); 
	root = insert(root, 10); 
	root = insert(root, 14); 
	root = insert(root, 22); 

	int k = 3; 
    cout<<"Sum of k smallest is " << ksmallestElementSum(root, k) << endl; 
	return 0; 
}

Output

Sum of k smallest element is 152

Explanation

1.First of all go to the root and compare k with lcount + 1 if it is equal then temp_sum = 208 and return otherwise if k < lCount then go the left child of the root.

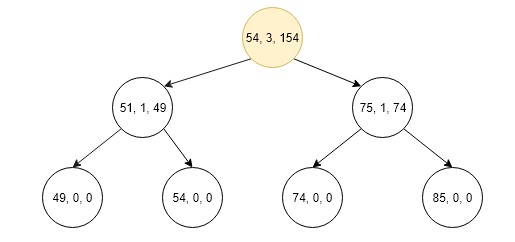
2.Now compare the lCount + 1 of current node with k if it is equal then temp_sum = 100 and return if k>lCount the go to right and temp_sum = 100 and k = 1.

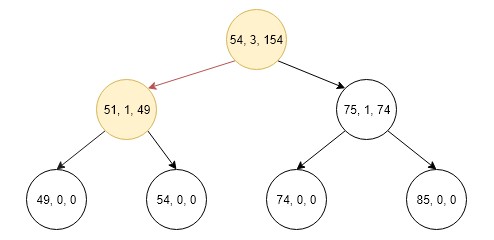
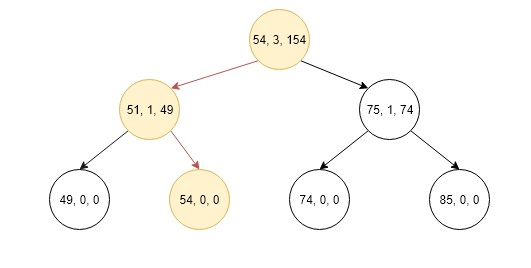
3.Now again compare lCount + 1 with k if it is equal then temp_sum = 152 and return.

Conclusion

The basic idea of augmenting a data strucure is to modify the existing data structure to solve our problem without degrading the overall performance of the data strucure.