Binary Lifting with k-th ancestor and lowest common ancestor (LCA)

Reading time: 30 minutes | Coding time: 12 minutes

The first step is to find out the 2j ancestor of every node where 0 <= j <= log(n). This can be done by dynamic programming.
The DP relation is given by:

    dp[i][j] = dp[dp[i][j-1]][j-1]

Where dp[i][j] denotes the 2j th ancestor of the node i. The expression essentially breaks down the path between a node and its ancestor into two parts. The following figure illustrates this relation

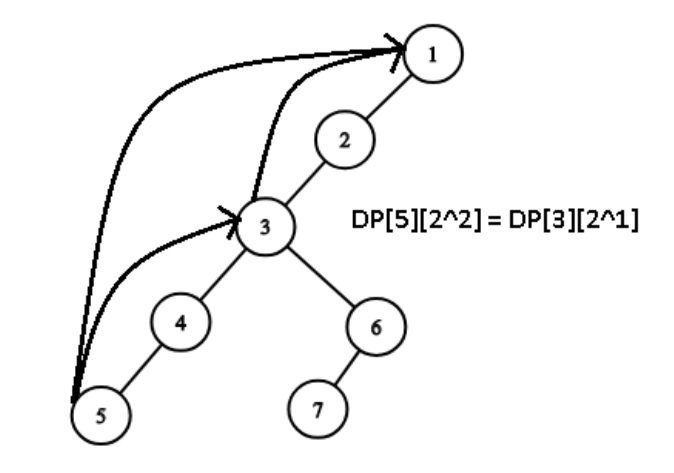
Note here that the fourth ancestor of Node 5 is the same as the second ancestor of Node 3.

To find the kth ancestor of a node, use the appropriate powers of two to sum up to the value k and move to the corresponding node in every step.

To find the LCA between two nodes a and b:

• Find the node at the lowest level (let us say a, otherwise swap them)
• Find the ancestor of a at the same level as b (let’s call this node c).
• Find the lowest ancestors of b and c which are not equal.
• Return the parent of one of the nodes found in step 3.

Pseudocode

The dp table can be computed by the following method:

	Precalculate():

		dp[i][j] = -1 for each pair i and j

for i = 1 to n
dp[i][0] = parent[i];

for h = 1 to logn
for i = 1 to n
If dp[i][h-1] not equal to -1
dp[i][h] = dp[dp[i][h-1]][h-1]

The k’th ancestor can be calculated as follows

Findkthancestor():	

	//find kth ancestor of currentNode

	for i = logn to 0
		If dp[currentNode][i] != -1 and 2^i <= k:
			currentNode = dp[currentNode][2^i]
			k = k - 2^i

	return currentNode 

The LCA between two nodes can be found as follows:

	FindLCA():

		//find lca between two nodes a and b

		If level[a] < level[b] 
			swap a and b

		c = a

		//find the ancestor of a at the same level of b
		for i = logn to 0
			If level[c] - 2^i >= level[b]
				c = dp[c][i]

		If b is equal to c
			return b

		for i = logn to 0
			If dp[b][i] != -1 and dp[b][i] != dp[c][i]
				b = dp[b][i]
				c = dp[c][i]

		return parent[b]

Complexity

Preprocessing :

• Best Case Complexity: O(N log N)
• Average Case Complexity: O(N log N)
• Worst Case Complexity: O(N log N)
• Memory Complexity: O(N log N)

Find kth ancestor:

• Best Case Complexity: O(log N)
• Average Case Complexity: O(log N)
• Worst Case Complexity: O(log N)
• Memory Complexity: O(1) (Ignoring dp table)

Find LCA between two nodes:

• Best Case Complexity: O(log N)
• Average Case Complexity: O(log N)
• Worst Case Complexity: O(log N)
• Memory Complexity: O(1) (Ignoring dp table)

Implementations

#include<bits/stdc++.h>
using namespace std;

// the total number of nodes in the tree
#define N 7

// log(N)
#define LG 5


//Find out the parent and level of each node using a depth first search
void dfs(int s, vector<int> graph[], int &depth, int parent[], int level[], int visited[]){
	
	visited[s] = 1;
	
	level[s] = depth;
	
	for(int i = 0; i < graph[s].size(); i++){
		if(!visited[graph[s][i]]){
		    
		    //going one level deeper
			depth++;
			
			dfs(graph[s][i], graph, depth, parent, level, visited);
			
		    parent[graph[s][i]]=s;
			
			//backtracking to the parent node
			depth--;
		}
	}
}

void findKth(int a, int k, int dp[][LG]){
    
    int c = a;
    
    int cur_level = k;
    
    for(int i = LG; i >= 0; i--){
        if(dp[c][i] != -1 && (1 << i) <= cur_level){
            c = dp[c][i];
            cur_level = cur_level - (1 << i);
        }
    }
    
    cout << "The " << k << "nd ancestor of " << a << " is " << c << '\n';
    
}

void lca(int a, int b, int level[], int dp[][LG], int parent[]){
	
	int lg;
	
	if(level[a]<level[b])
	    swap(a,b);
	
	//calculate the maximum value of height we might need
	for(lg =0 ; (1<<lg) <= level[a]; lg++);
	
	
	// find the ancestor of a at the same level of b
	for(int i = lg - 1; i >= 0; i--)
		if((level[a] - (1<<i)) >= level[b]){
			a = dp[a][i];
		}
		
	if(a == b){
	    cout << "The lowest common ancestor of a and b is " << a << '\n';
        return;
	}
	
	// find the lowest ancestors of a and b which are not equal
	for(int i = lg; i >= 0; i--){
		if(dp[a][i] != dp[b][i]){
			a = dp[a][i];
			b = dp[b][i];
		}
	}
	cout << "The lowest common ancestor of a and b is " << parent[a] << '\n';
}

void precalculate(int dp[N][LG], int parent[]){

    
    
    //initialize 2^0 th ancestor as parent
    for(int i = 0; i < N; i++)
        dp[i][0] = parent[i];
    
    for(int h = 1; h < LG; h++){
        for(int i = 0; i < N; i++){
            if(dp[i][h-1] != -1)
                dp[i][h] = dp[dp[i][h-1]][h-1];
        }
    }
    
}
int main(){
    
    //adjacency list to store the graph
    vector<int> graph[N];
    
    int parent[N], level[N], visited[N], dp[N][LG];
    
    //intialize all arrays with zero
    memset(parent, 0, sizeof(parent));
    memset(level, 0, sizeof(level));
    memset(visited, 0, sizeof(visited));
    
    
    //initialize dp table with -1(which denotes unreachable ancestor)
    memset(dp, -1, sizeof(dp));
    
    /* create an undirected graph of the structure:
            0
          /   \
         1     2
        / \   / \
       3   4 5   6
    */
    
    
    graph[0].push_back(1);
    graph[1].push_back(0);
    graph[0].push_back(2);
    graph[2].push_back(0);
    graph[1].push_back(3);
    graph[3].push_back(1);
    graph[1].push_back(4);
    graph[4].push_back(1);
    graph[2].push_back(5);
    graph[5].push_back(2);
    graph[2].push_back(6);
    graph[6].push_back(2);
    
    
    int depth = 0;
    dfs(0, graph, depth, parent, level, visited);
    
    precalculate(dp, parent);
    
    //find out the 2nd ancestor of node 3
    findKth(3, 2, dp);
    
    //find LCA of 5 and 6
    lca(5, 6, level, dp, parent);
    
    
}

Applications:

• LCA is used in compiler design to find the LCA of two basic blocks so that some basic computation can be inserted into the ancestor and it is available for both of them.
• Used in computer graphics to find out the smallest cube which contains two given cubes.
• LCA can be used to find the most specialised superclass which has been inherited by two different classes.