
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 15 minutes
Linear Regression is a simple yet effective prediction that models any data to predict an output based on the assumption that it is modeled by a linear relationship. This algorithm searches the Regression line, which is nothing more than a straight line, considering the mean of all values matched by the correlation between the variables. It is used to predict values and is simple to use.
In this guide, we will implement Linear Regression in Python with TensorFlow
TensorFlow
In Python, we have many libraries that was created to help Data Scientists to do their jobs. That is why this language is so many used and his user base is growing. With a few lines of code, you call multiple functions in order to achieve the result you need. Among all the libraries, we have TensorFlow which can be used for many Machine Learning applications and we can use it to do a Regression.
In this article I will show you a Linear Regression case, using TensorFlow.
During the code explanation, there are explanations about the key terms.
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
First we start importing some libraries, Numpy for create the arrays, TensorFlow to do the regression and Matplotlib to plot data.
x = np.linspace(0, 25, 100)
y = np.linspace(0, 25, 100)
# Adding noise to the random linear data
x += np.random.uniform(-4, 4, 100)
y += np.random.uniform(-4, 4, 100)
n = len(x) # Number of data points
Now we have to generate a random linear data. In this case we will have 100 data points ranging from 0 to 25.
plt.scatter(x, y)
plt.xlabel('x')
plt.xlabel('y')
plt.title("Training Data")
plt.show()
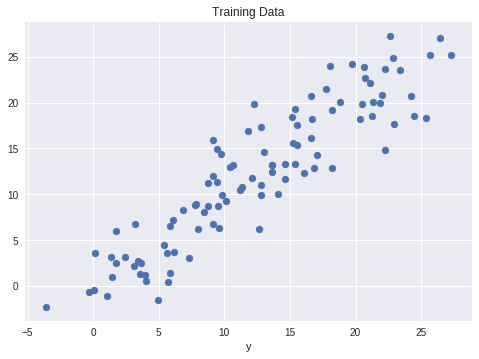
Plot the Training Data
X = tf.placeholder("float")
Y = tf.placeholder("float")
Creating our model by defining the placeholders X and Y. Declaring X and Y as placeholders mean that we need to pass in values at a later time.
Placeholder?
A placeholder works like anyother variable, but it doesn´t need a initial value.
W = tf.Variable(np.random.randn(), name = "W")
b = tf.Variable(np.random.randn(), name = "b")
Definition of our W (weight) and b (bias) using random values.
learning_rate = 0.01
training_epochs = 1000
Definition of our hyperparameters
Learning Rate?
Learning rate is a hyper-parameter that controls how much we are adjusting the weights of our network with respect the loss gradient.
Epoch?
An epoch is a full iteration over samples.
# Hypothesis
y_pred = tf.add(tf.multiply(X, W), b)
# Mean Squared Error Cost Function
cost = tf.reduce_sum(tf.pow(y_pred-Y, 2)) / (2 * n)
# Gradient Descent Optimizer
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
# Global Variables Initializer
init = tf.global_variables_initializer()
Creation of the Hypothesis, Cost Function and the Optimizer.
Hypothesis?
This is the relationship betweent x and y.
Cost Function?
This formula is used to determine the value of the weight and bias from the given dataset.
Gradient Descent Optimizer?
It is an alghoritm that is used to find the optimized paramaters.
# Starting the Tensorflow Session
with tf.Session() as sess:
# Initializing the Variables
sess.run(init)
# Iterating through all the epochs
for epoch in range(training_epochs):
# Feeding each data point into the optimizer using Feed Dictionary
for (_x, _y) in zip(x, y):
sess.run(optimizer, feed_dict = {X : _x, Y : _y})
# Displaying the result after every 50 epochs
if (epoch + 1) % 50 == 0:
# Calculating the cost a every epoch
c = sess.run(cost, feed_dict = {X : x, Y : y})
print("Epoch", (epoch + 1), ": cost =", c, "W =", sess.run(W), "b =", sess.run(b))
# Storing necessary values to be used outside the Session
training_cost = sess.run(cost, feed_dict ={X: x, Y: y})
weight = sess.run(W)
bias = sess.run(b)
Output:
Epoch: 50 cost = 5.8868036 W = 0.9951241 b = 1.2381054
Epoch: 100 cost = 5.7912707 W = 0.99812365 b = 1.0914398
Epoch: 150 cost = 5.7119675 W = 1.0008028 b = 0.96044314
Epoch: 200 cost = 5.6459413 W = 1.0031956 b = 0.8434396
Epoch: 250 cost = 5.590799 W = 1.0053328 b = 0.7389357
Epoch: 300 cost = 5.544608 W = 1.007242 b = 0.6455922
Epoch: 350 cost = 5.5057883 W = 1.008947 b = 0.56222
Epoch: 400 cost = 5.473066 W = 1.01047 b = 0.48775345
Epoch: 450 cost = 5.4453845 W = 1.0118302 b = 0.42124167
Epoch: 500 cost = 5.421903 W = 1.0130452 b = 0.36183488
Epoch: 550 cost = 5.4019217 W = 1.0141305 b = 0.30877414
Epoch: 600 cost = 5.3848577 W = 1.0150996 b = 0.26138115
Epoch: 650 cost = 5.370246 W = 1.0159653 b = 0.21905091
Epoch: 700 cost = 5.3576994 W = 1.0167387 b = 0.18124212
Epoch: 750 cost = 5.3468933 W = 1.0174294 b = 0.14747244
Epoch: 800 cost = 5.3375573 W = 1.0180461 b = 0.11730931
Epoch: 850 cost = 5.3294764 W = 1.0185971 b = 0.090368524
Epoch: 900 cost = 5.322459 W = 1.0190892 b = 0.0663058
Epoch: 950 cost = 5.3163586 W = 1.0195289 b = 0.044813324
Epoch: 1000 cost = 5.3110332 W = 1.0199214 b = 0.02561663
Starting the TensorFlow session, initializing the variables and showing the results of each 50 epochs.
predictions = weight * x + bias
print("Training cost =", training_cost, "Weight =", weight, "bias =", bias, '\n')
Calculating and printing the prediction
Output:
Training cost = 5.3110332 Weight = 1.0199214 bias = 0.02561663
Output of the prediction
# Plotting the Results
plt.plot(x, y, 'ro', label ='Original data')
plt.plot(x, predictions, label ='Fitted line')
plt.title('Linear Regression Result')
plt.legend()
plt.show()
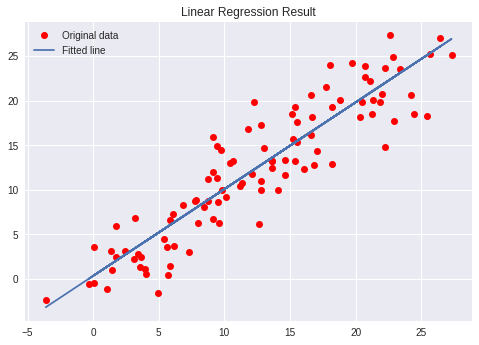
Plot of the result, with the Regression Line.
