Boolean Parenthesization Problem

We will solve Boolean Parenthesization Problem using Dynamic Programming and understand the algorithm with a step by step explanation. The time complexity to solve this problem is O(N^3) with a space complexity of O(N^2).

Given a boolean expression with following symbols.:

• 'T' ---> true
• 'F' ---> false

And following operators filled between symbols

• & ---> boolean AND
• | ---> boolean OR
• ^ ---> boolean XOR

Count the number of ways we can parenthesize the expression so that the value of expression evaluates to true.
Let the input be in form of two arrays one contains the symbols (T and F) in order and other contains operators (&, | and ^}

Explanation:

Let S1: "TFTF" and S2: &| ^

S2 length is one less than S1. Such that the final string formed is T&F|T^F
By boolean algebra following are true:

T & T = T		T|T= T			T^T= F
T & F = F		T|F= T			T^F= T
F & F = F		F|T= T			F^T= T
F & T = F		F|F= F			F^F= F

Suppose in the above given string T&F yields 3 ways to produce 3 trues, and 2 falses:
And T^F yields 2 ways to produce True and 3 ways to produce false.
So the total ways to produce True in the given string is
3* 2(true of first half and true of second half)= 6
3* 3(true of first have and false of second half)= 9
2* 2(false of first have and true of second half)=4
Because the OR(|) operation yields true in 3 conditions(true and true, false and true, true and false), therefore total ways to produce true in the given string would be 19 by the example above.

Take:

• ltc- left side true count
• lfc- left side false count
• rtc- right side true count
• rfc- right side false count

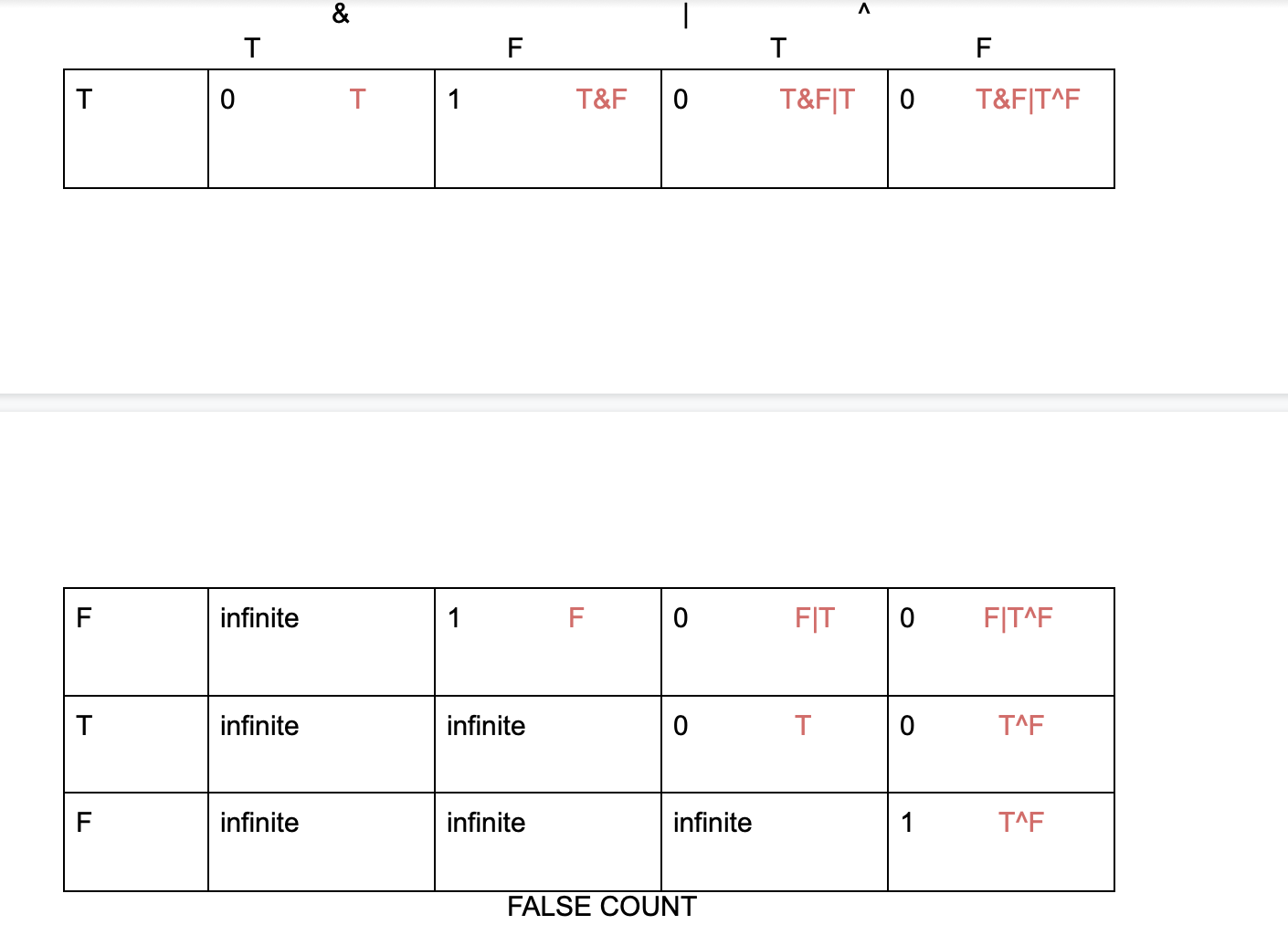
Now we draw two DP tables, one for true count and the other for false counts.

**Filling the Dp tables, **

• T&F never producee true , so we fill 0 in that marked cell in true count dp table.
• T&F produces false once , so we fill 1 in that marked cell in the false count dp table.
• F|T produces true once, so we will fill 1 in that marled cell in the true count dp table.
• F|T never produces false, so we will fill 0 in that marled cell in the false count dp table.
• T^F produces true once, so we will fill 1 in that marled cell in the true count dp table.
• T^F never produces true, so we will fill 0 in that marled cell in the false count dp table.
• Also for T in true count dp table, it produces true once only and false will never produce true
• In the True count dp table.
• Also for F in False count dp table, it produces false once only and false will never produce true In the True count dp table.

Now for other cells,

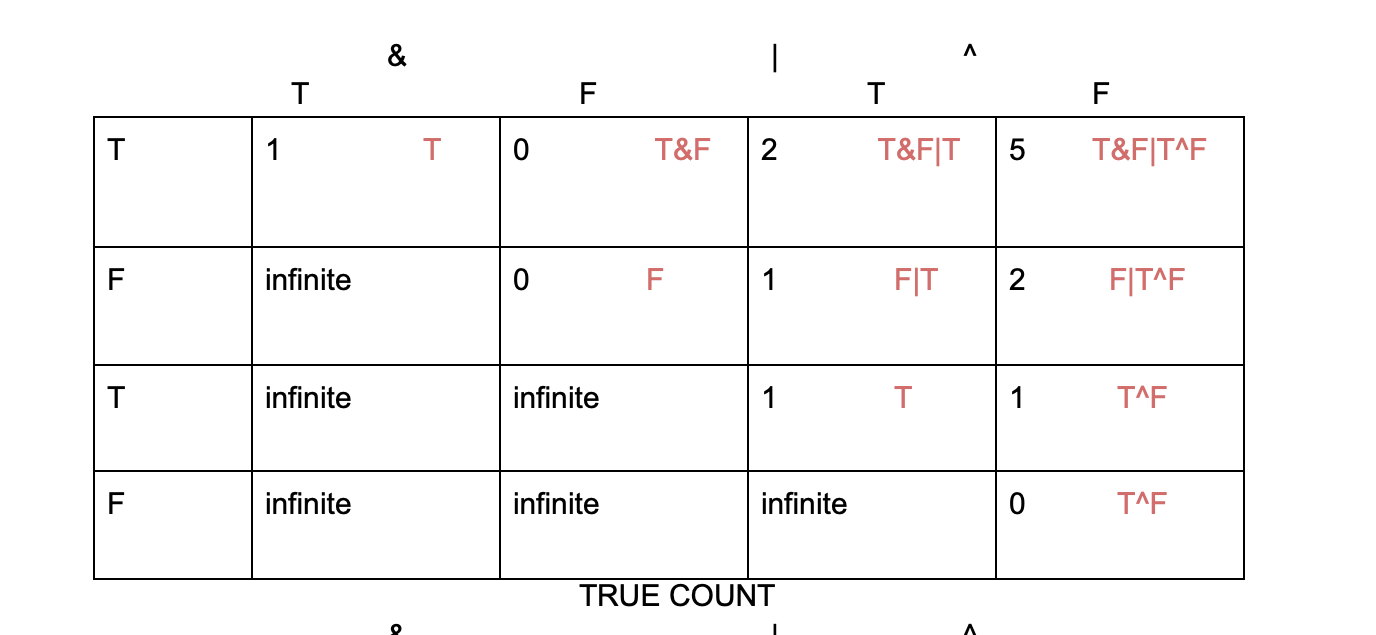
1. T&F|T: (T&F)|T and T&(F|T)

T&(F|T)-        true count 

ltc* rtc     -  1* 1     =  1
		
		False count 
ltc* rfc  + lfc* rtc +lfc* rfc -            1* 0 + 0* 1 + 1* 0 =  0

(T&F)|T-        true count 

ltc* rtc+ ltc* rfc+ lfc* rtc     -  0* 1 + 0* 0 +1* 1     =  1
		
		False count 
 lfc* rfc -            1* 0  =    =0

Total true count-  1+1 = 2
Total false count-   0+0= 0

2. (F|T)^F: true count

ltc* rfc +lfc* rfc  -      1* 1 +0* 1 =    1

False count	
lfc* rfc +ltc* rtc-        0* 1 + 1* 0 =    0
  
F|(T^F) -              	true count

ltc* rft +ltc* rfc +lfc* rtc -      0* 1 +0* 0 + 1* 1 =    1

False count	
lfc* rfc-         1* 0 =    0

Total true count = 1+1 =2 
Total false count = 0+0 =0

3. (T&F|T^F)- T&(F|T^F) and (T&F)|(T^F) and (T&F|T)^F

T&(F|T^F)			true count

ltc* rtc  -      1* 2 =    2

False count	
lfc* rtc+ ltc* rfc+lfc* rfc -        1* 0 + 0* 2 +0* 0 =    0

(T&F)|(T^F)

true count

ltc* rtc + ltc* rfc + rtc* lfc  -      0* 1 + 0* 0 + 1* 1 =    1

False count	
lfc* rfc -        1* 0 =    0
  
(T&F|T)^F

true count

ltc* rfc + lfc* rtc -     2* 1 + 0* 0 =    2

False count	
lfc* rfc + ltc* rtc  -        0* 1+ 2* 0=    0


Total true count- 2+1+2 =  5
Total false count-  0+0+0+0= 0

BASE CASE

Filling the cells of the DP tables, with 1 and 0.
In the true count DP table, we fill the ,cells with T, as 1, and with F as 0,
and vice versa in the false count DP table.

for (int i = 0; i < n; i++) 
{
    F[i][i] = (symb[i] == 'F') ? 1 : 0;
    T[i][i] = (symb[i] == 'T') ? 1 : 0;
}

Recursion for True Dp table-

T and F are two DP arrays, for true count and false count respectively.

For the recursion relations, for when the operator is &,

T(i,j)  = Summation ( T(i,k) * T(k+1,j)) 

for all k such that i < k < j

For the recursion relations, for when the operator is |,

T(i,j) = sum ( Total(i,j) - F(i,k)* F(k+1,j)) 

for k such i < k

For the recursion relations, for when the operator is XOR,

T(i,j) = sum(T(i,k)* F(k+1,j) + F(i,k)* T(k+1,j)) 

for k such i < k

k=i is the subsript of summation and j-1 is the superscript

T(i,j) = ∑(k=i)(j-1)  {    T(i,k)* T(k+1,j) 	if operator k is ‘&’

Total(i,k) * Total(k+1,j) - F(i,k)* F(k+1,j)    if operator  k  is ‘|’

T(i,k) * F(k+1,j) +F(i,k) * T(k+1,j)  		    if operator k is ‘xor’  }

Total(i,j)= T(i,j)+ F(i,j)

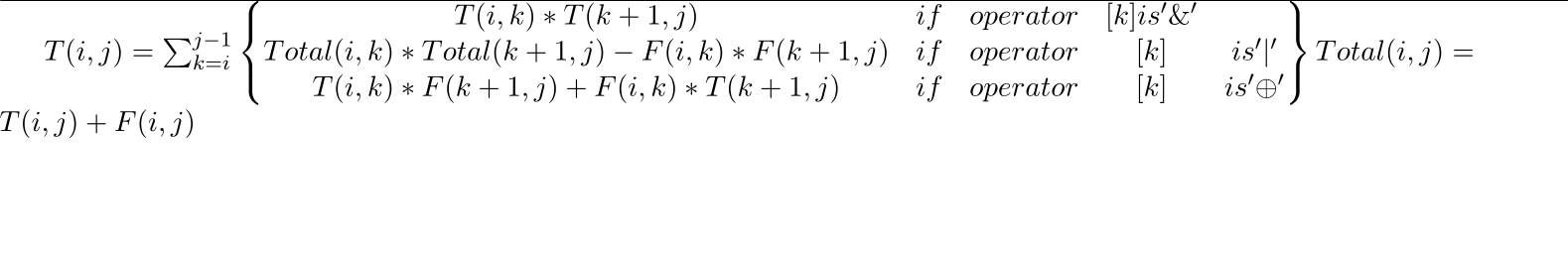
Recursion for False Dp table-

For the recursion relations, for when the operator is &,

F(i,j) = Sum ( Total (i,j) - T(i,k)* T(k+1))

for all k for i< k< j

For the recursion relations, for when the operator is |,

F(i,j) = Summation (F(i,k)* F(k+1,j)) 

for all  i < k < j

For the recursion relations, for when the operator is XOR,

F(i,j) = sum(T(i,k)* F(k+1,j) + F(i,k)* T(k+1,j)) 

for k such i < k

k=i is the subsript of summation and j-1 is the superscript

T(i,j) = ∑(k=i)(j-1)  {    F(i,k)* F(k+1,j) 		if operator k is ‘|’
 Total(i,k) * Total(k+1,j) - T(i,k)* T(k+1,j)       if operator  k  is ‘&’
T(i,k) * T(k+1,j) +F(i,k) * F(k+1,j)  		        if operator k is ‘xor’  }

Total(i,j)= T(i,j)+ F(i,j)

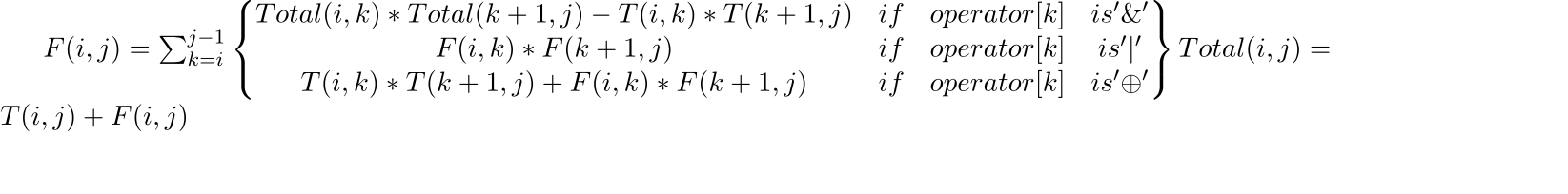
CODE FOR THE PROGRAM-

class boolparenthesis
{
 
    static int counter(char symb[],
                            char oper[],
                            int n)
    {
        int F[][] = new int[n][n];
        int T[][] = new int[n][n];
 
        for (int i = 0; i < n; i++) {
            F[i][i] = (symb[i] == 'F') ? 1 : 0;
            T[i][i] = (symb[i] == 'T') ? 1 : 0;
        }
 
        for (int g1 = 1; g < n; ++g1)
        {
            for (int i = 0, j = g1; j < n;++i, ++j)
            { T[i][j] = F[i][j] = 0;
                for (int g = 0; g < g1; g++)
                 
                { int k = i + g;
 
                    int tpp = T[i][k]+ F[i][k];
                    int tkj = T[k + 1][j] + F[k + 1][j];
 
                    if (oper[k] == '&')
                    {
                        T[i][j] += T[i][k]* T[k + 1][j];
                        F[i][j]+= (tpp * tkj- T[i][k]* T[k + 1][j]);
                    }
                    if (oper[k] == '|')
                    {
                        F[i][j] += F[i][k]* F[k + 1][j];
                        T[i][j]+= (tpp * tkj- F[i][k]* F[k + 1][j]);
                    }
                    if (oper[k] == '^')
                    {
            T[i][j] += F[i][k]* T[k + 1][j]+ T[i][k]* F[k + 1][j];
        F[i][j] += T[i][k]* T[k + 1][j]+ F[i][k]* F[k + 1][j];
                    }
                }
            }
        }
        return T[0][n - 1];
    }
 
    public static void main(String[] args)
    {
        char symbol[] = "TTFT".toCharArray();
        char operator[] = "|&^".toCharArray();
        int n = symbol.length;
               System.out.println(
            counter(symbol, operator, n));
    }
}

Runtime for the algorithm-

Time Complexity: O(N^3) by the three for loops
Auxiliary Space: O(N^2)