Count all subsequences in an array with product less than K

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

Reading time: 25 minutes | Coding time: 10 minutes

Finding subsequences in an array with product less than a given number is another area of application of Dynamic programming. Our aim is to find the combinations of elements that when multiplied give the product less than an arbitrary number K. We can either go about it by brute-forcing through all the elements which will require a lot of time and calculations, or we can make use of dynamic programming to break this down into smaller sub-problems and use the result of each to build up to our solution.

Introduction

In order to find the number of subsequences that will give the product less than the given number, we create a matrix whose row represents different values of K and each column contains the maximum possible number of elements from original array that will give the product less than K.

Every column represents the first j number of elements taken from the original array. This makes it easier as we already have the result available from previous column, so for our j^th column we have the number of available sequences from j-1 elements and now only need to calculate subsequences when we introduce the j^th element. Thus, at every step our calculation is reduced and we are able to make use of previously calculated results to arrive at newer results. Now in every column j we have the number of sequences formed from j-1 elements plus the number of sequence formed with j elements.

Method

We arrive at the question as to how we will find the number of sequences with j^th element introduced after we have calculated the number for j-1 elements. The number of these subsequences is already present within our matrix and simply needs to be added over the number of sequences we found previously using j-1 elements. The location for the cell where the number of subsequences with j elements will be located is given through -

(floor(i/arr[j-1])^th row and (j-1)^th column) + 1

where i represents the current row number, arr[] is our original array and j is the index of the current column.

The floor operation is used to round off the lower value since matrix rows are numbered as discrete integers. The (i/arr[j-1])^th row is calculated through the premise that before adding (j-1)^th element our product was i so in the current column(j-1), we have to locate subsequences x such that we can multiply the (j-1)^th element to them and the product will not exceed K.

Basically, we have X such subsequences to which we can multiply the (j-1)^th element from the array and the result will be lesser than or equal to i. Simplifying further, when we divide the current target product(row number) by the last element, we only need to check the number of subsequences that have product lesser than or equal to that result from our array, which we have already done. Since our element gave a product that is less than or equal to current target, that must mean the element also is less than or equal to i, so the +1 for having a subsequence of only the (j-1)^th element alone.

Algorithm

Create a matrix with K rows and N columns, where N is the length of our array, and fill with zeros.
For every element that is smaller than K :
- add previous element
- add the (i/array[j-1])^th element where i is current row and j is current column
- add 1
The last element of the matrix contains the total number of subsequences.

Example

Let us take an array [1,2,3,4]
with K = 10
The subsequences formed here will be:

[{1} ,{2} ,{1, 2}, {3}, {1, 3}, {2, 3}, {1, 2, 3}, {4}, {1, 4}, {2, 4}, {1, 2, 4}]

(not accounting for permutations with redundant elements)
The total number of subsequences here is 11

The matrix formed is :

mtrx

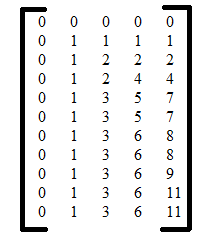
Here, let us assume we have to calculate number of subsequences from first three term such that product is less than 7. Now, j=3 and i=7.

Which means we calculate the result using only the first three elements from the array. Now, we see at matrix[7][2] we have 3 subsequences using 2 elements which give a product less than 7, so we can include these in our current assessment. Now to find how many subsequences would possibly give a product less than 7, we divide 7 by the 3rd element of the array i.e. floor(7/3) which is equal to 2. So, in the current column, we have number of subsequences that give a result less than or equal to 7/3 as 2, we add this to the current result, and add 1 for the number itself.

Thus we have:

3 + matrix[floor(7/3)][2] + 1 = 3 + 2 + 1 = 6

We get 6 possible subarrays that have a product less than 7, and these are:

[{1},{2},{1,2},{3},{1,3},{1,2,3}]

Pseudocode

note: we are using 1 based indexing to simplify the operation and make it easier to understand.

function subSequence(array, length, k){
	for(i=0 to length+1)
		for(j=0 to k+1)
			matrix[i][j] = 0
	for(i=1 to k+1)
		for(j=1 to n+1)
			matrix[i][j] = matrix[i][j-1]  
			if(array[j-1] <= i and array[j-1] > 0) 
				matrix[i][j] = matrix[i][j] + matrix[floor(i/array[j-1])][j-1] + 1
	return matrix[k][length]

Note: To change from less than or equal to strictly less than K, simply change to if(array[j-1] < i)

Implementation

C++
Python

C


   #include <bits/stdc++.h> 
   using namespace std;
   int subSeqence(vector &array, int n, int k){  
       int matrix[k + 1][n + 1]; 
       memset(matrix, 0, sizeof(matrix)); 
       for (int i = 1; i <= k; i++){ 
           for (int j = 1; j <= n; j++){  
               //number of subsequence using j-1 terms 
               matrix[i][j] = matrix[i][j - 1]; 
               // if matrix[j-1] < i the product is definitely greater than i 
               if (array[j - 1] <= i && array[j - 1] > 0) 
                   // number of subsequence from 1 to j-1 terms plus the j^th term
                   matrix[i][j] += matrix[i/array[j-1]][j-1] + 1; 
           } 
       } 
           return matrix[k][n]; 
   }
   

   int main(){
       vector<int> A;
       int i, n, x, k;
       cout << "How many elements in the array? ";
       cin >> n;
       for(i=0; i < ;n; i++){
           cout << "Enter a number: ";
           cin >> x;
           A.push_back(x);
       }
       cout << "Enter limit of product for subsequences: ";
       cin >> k; 
       cout << subSeqence(A, n, k) << endl; 
   }

C++


   def subSequence(array, n, k):  
       matrix = [[0 for i in range(n + 1)] for j in range(k + 1)]              
       for i in range(1, k + 1): 
           for j in range(1, n + 1):    
               #number of subsequence using j-1 terms  
               matrix[i][j] = matrix[i][j - 1]    
               #if matrix[j-1] < i the product is definitely greater than i   
               if array[j - 1] <= i and array[j - 1] > 0: 
                   #number of subsequence from 1 to j-1 terms plus the j^th term  
                   matrix[i][j] += matrix[i // array[j - 1]][j - 1] + 1
        return matrix[k][n]
   

   array = []
   n = input("How many elements in the array? ")
   array.append(input("Enter a number: ") for _ in range n)
   k = input("Enter limit of product for subsequences: ")
   subSequence(array, n, k)

Note: You can use numpy array instead of python's default list type to speed up larger calculations

Complexity

Time complexity: Θ(KN)
Space complexity: Θ(KN)

Where N is length of our array