Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 40 minutes | Coding time: 10 minutes
Understand the problem we have solved in this article:
- if a[i]>a[j] for i<j then pair (i,j) is called inversion of an array.
- Number of Inversion in array is indicated how far array is sorted.
- Inversion is number of steps required to apply on array to get it sorted.
- If array is already sorted then number of inversion is 0.
- If array is sorted in descending then number of inversion in array will maximum.
- We can use Merge Sort to find inversion in array but Fenwick tree is easier way to count inversion in array compare to Merge Sort.
- If you don't about Fenwick tree then go to [Fenwicktree] (https://iq.opengenus.org/p/bd991645-36f7-4142-a2e6-b21e6122919d/) before further reading this post.
Fenwick tree is usually used for range query problems but it can be used to solve the problem of finding the number of inversions in an array efficiently.
Steps to find number of inversion :
- convert(map) an elements of an array with in range [1,..n] (n is size of an array).We do this due to following reason .
- Array elements can be negative. We use value of an array elements to count inversion. We passed value of array element as an index for Fenwick tree. index can not be negative.
- Elements of array are not uniformly distributed. so we have to create an Fenwick tree whose size is =maximumelement+1.
- to map an array between [1,..n] we first sort the array.
- create an one hashmap.
- Traverse in array and store mapping of numbers and their values (in converted array) in hash table.
- Traverse given array and change elements to their positions using hash table.
- This convert process will take O(nlogn) time.
- count the number of inversions in an array by traversing the array from N-1 to 0. When we are at the position array[i] we count the numbers that are less than array[i] at that point. We get this count from the sum() method of the Fenwick tree.
- update the value in Fenwick tree using update(index i) method.
- Example :
- Input array ={1,-9,5,4,3}.
- convert(map) an elements of an array with in range [1,..n]

- Initial Fenwick tree
- count the number of inversion in array by traversing the array from N-1 to 0. update value in Fenwick tree .
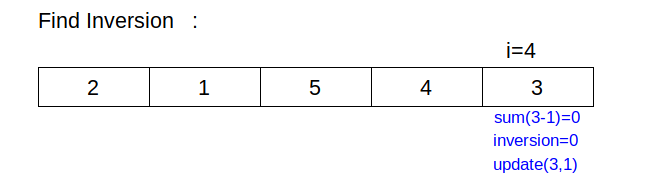
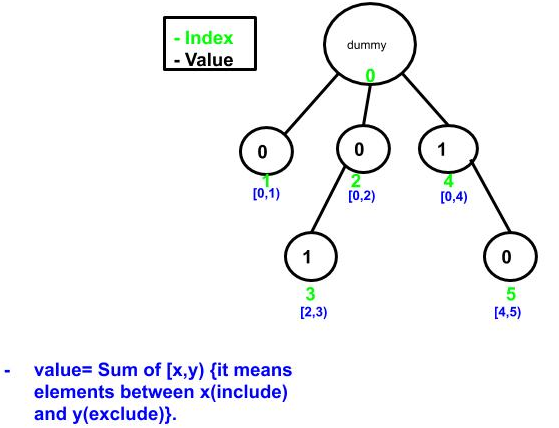
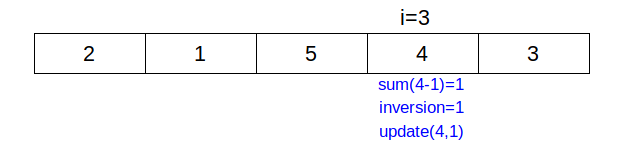
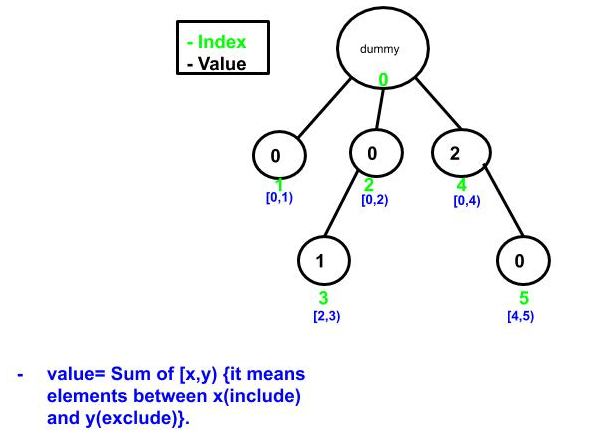

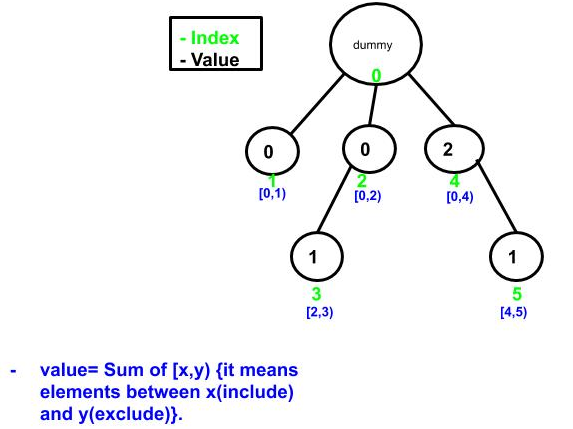
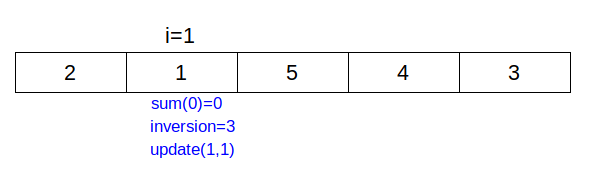
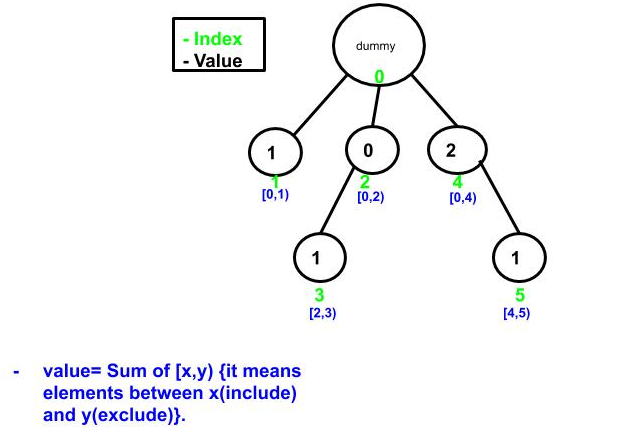
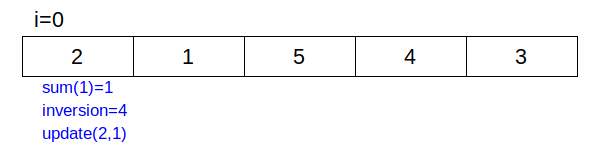
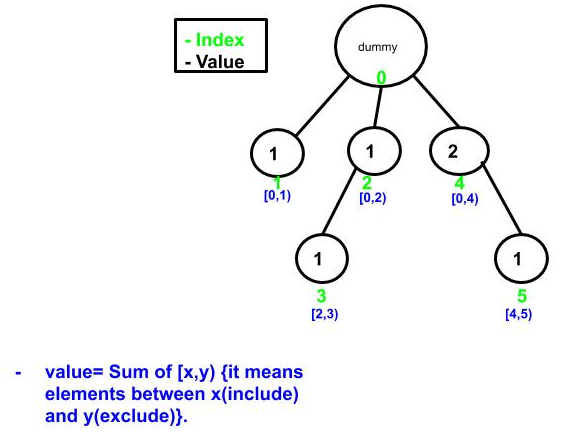
- Input array ={1,-9,5,4,3}.
Implementation :
import java.util.Arrays;
import java.util.HashMap;
public class FenwickInversion {
public static int n=0;
public static int FT[];
public static void main(String[] args) {
int a[] = {1,-9,5,4,3};
int p[]=a.clone();
n=a.length;
FT =new int[n+1];
System.out.println("Input array :"+Arrays.toString(a));
System.out.println("Number of Inversions in given input array :" +inversions(a,n));
clearFT(); // clear Frnwick tree
Arrays.sort(p);
System.out.println("number of Inversions in sorted(ascending order) array :"+inversions(p,n));
int desc[] = {5,4,3,1,-9};
clearFT(); // clear Fenwick tree
System.out.println("number of Inversions in sorted(descending order) array :"+inversions(desc,n));
}
public static int [] convert(int arr[]) //convert(map) an array in [1,..n] example [1,-3,5,4]
{ // will convert into [2,1,4,3].
int tmp[]=arr.clone();
Arrays.sort(tmp); //sort an array in ascending order
HashMap<Integer,Integer> map =new HashMap();
int value=1;
for(int j=0; j<tmp.length; j++)
map.put(tmp[j], value++); // we map the array in [1,...n]
for (int i =0; i<map.size(); i++)
arr[i] = map.get(arr[i]); //store the new value (mapped) value into array
return arr;
}
public static void construct(int arr[]) // create a fenwick tree of given array
{
for(int i=0; i<=n; i++) // intitalize all node with zero
{
FT[i]=0;
}
// Store the values in FT[] using update()
for(int i=0; i<n; i++)
update(i,arr[i]);
}
public static void update(int i,int value) // add value to element with index i
{
while(i<=n)
{
FT[i]+=value;
i=i+(i&(-i));
}
}
public static int sum(int i) // returns the sum of input array[0,..i]
{
int sum=0;
while (i>0)
{
sum+=FT[i];
i=parentnode(i);
}
return sum;
}
public static int parentnode(int i) // returns the parent node(index) of index i
{
int index = i-(i&(-i));
return index;
}
public static int inversions(int arr[],int n) // returns the number of inversion in array
{
int inversion=0;
convert(arr);
for(int i=n-1; i>=0; i--)
{
inversion+=sum(arr[i]-1); //// count the elements smaller than arr[i]
update(arr[i],1); // add current element into FT[]
}
return inversion;
}
public static void clearFT()
{
FT=null;
FT=new int[n+1];
}
}
Output :
Input array :[1, -9, 5, 4, 3]
Number of Inversions in given input array :4
number of Inversions in sorted(ascending order) array :0
number of Inversions in sorted(descending order) array :10
Complexity :
- array conversion will take O(nlogn). (it will depend on the sorting algorithm you use).
- sum and update function take O(logn). we are traversing over n elements so overall time complexity is O(nlogn).
Application :
- Based on the number of inversion in array we should that are is sorted or not.
- number of inversion we could find the number of step require to sort an array.