
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will explore stack and its properties and operation, then we will cover recursion and explain why stack is used for recursion, finally we will discuss how to convert recursive to iterative approach.
Table of contents:
- Introduction to Stack
- Add Elements into Stack
- Delete Elements from Stack
- Recursion
- Stack for Recursion
- Converting Recursive to Iterative Approach
In short, the Data Structure used for Recursion is Stack (LIFO) Data Structure.
Pre-requisites:
Introduction to Stack
Stack is one of the most fundamental data structures in computer science. It's called that because that's the exact best metaphor. Suppose we want to store 6 cubes one by one, we would probably organize them into a neat stack to efficiently use shelf space. Illustration is as followed:

The picture above shows that if we want to add additional cube to the stack, where would we add it? To the top of the stack or at the bottom? Of course we should add it at the top since adding it to the bottom would involve moving the entire stack.
What if we want to dispense a cube? Again, where would we take it from? Would we grab the cube at the top of the stack or would we move every other cube on the heavy stack to take the cube from the very bottom? I think most of us would add cubes to and take cubes from the top of the stack.
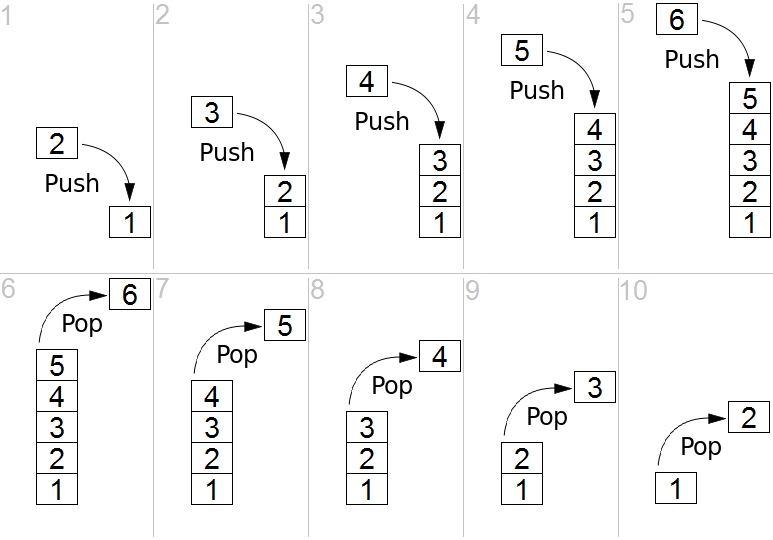
The operations mentioned above is what a computer stack ADT emulates. The behavior of the stack implies that the most recently added item will always be the first thing removed therefore a stack is referred to as a "last-in / first-out", or LIFO data type. For a Stack ADT the essential functions are called push() and pop(). Push() adds the value to top of the stack and pop() removes and returns that value at the top of the stack.
Add Elements into Stack
If we want add an element into a stack, we should add it at the top, and we name this operation as push():
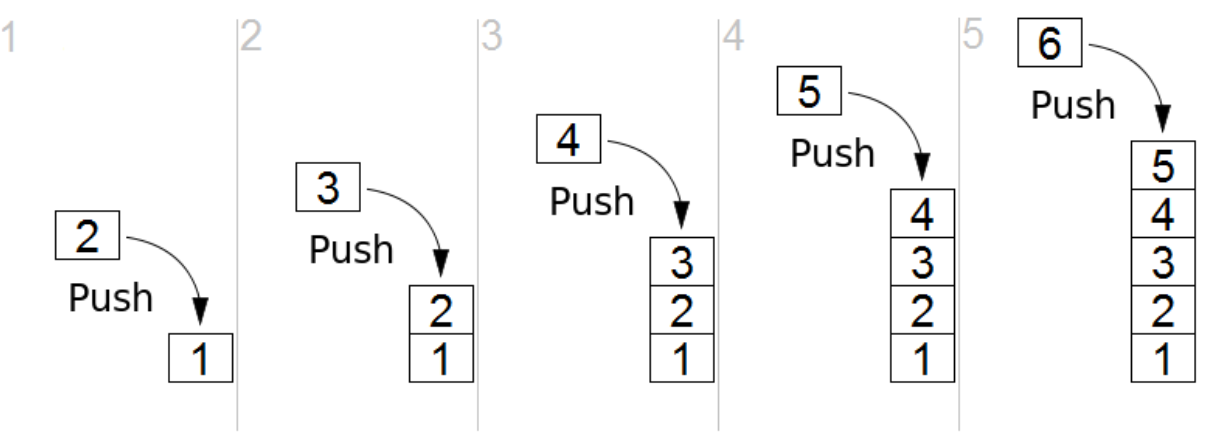
Sample code -- example of implementing the push():
Python
class Stack:
def __init__(self, size):
''' Constructor
Parameters:
self -- the current object
size -- the initialize size of our stack
'''
self.data = [0] * size
self.end = 0
def push(self, item):
''' push -- adds something to the top of the stack
Parameters:
self -- the current object
item -- the item to add to the stack
Returns nothing
'''
if self.end >= len(self.data):
print("Full!")
return
self.data[self.end] = item
self.end += 1
Delete Elements from Stack
If we want delete an element from a stack, we should take it at the top, and we name this operation as pop():
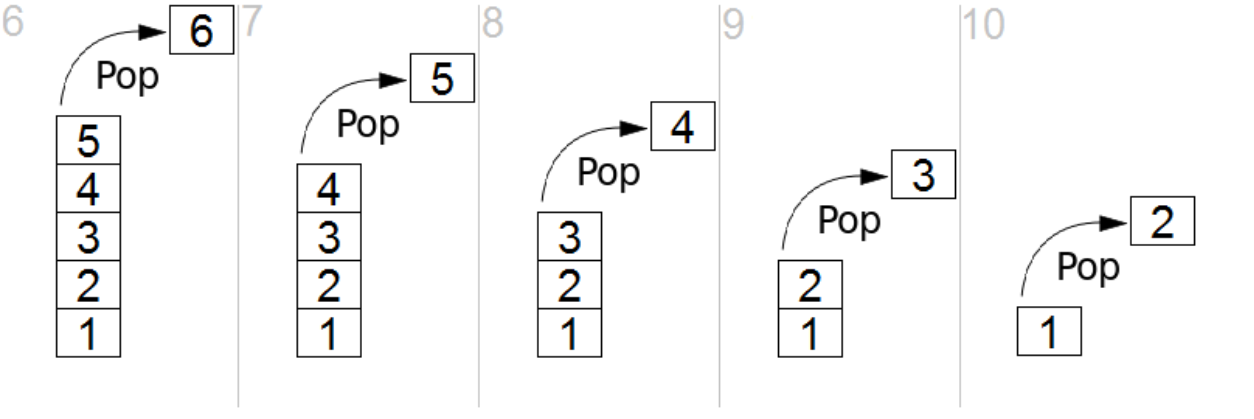
Sample code -- example of implementing the pop():
Python
class Stack:
def __init__(self, size):
''' Constructor
Parameters:
self -- the current object
size -- the initialize size of our stack
'''
self.data = [0] * size
self.end = 0
def push(self, item):
''' push -- adds something to the top of the stack
Parameters:
self -- the current object
item -- the item to add to the stack
Returns nothing
'''
if self.end >= len(self.data):
print("Full!")
return
self.data[self.end] = item
self.end += 1
def pop(self):
''' pop -- removes something from the top of the stack
Parameters:
self -- the current object
Returns the top element after removing it from the stack
'''
if self.end <= 0:
print("Empty!")
return
self.end -= 1
return self.data[self.end]
Recursion
Recursion is a concept that many people seem to struggle with. However, what is exactly recursion? Basically, recursion is a successive application of a rule or process multiple times to achieve the answer to a large problem. It does this by starting with the basic answer to most trivial version of the problem and then repeatedly applying a process where each success application generates the solution to an incrementally larger version of the same problem.
The idea of recursion is that we have a problem to solve, and we are looking for a way to solve this problem by demonstrating that the final answer is the result of applying a set of sequential computations to the result of solving a smaller version of the same problem. Since the smaller problem is the same type, the solution for that in turn comes from the same process applied to an even smaller version of problem.
Generally speaking, recursion involves two stages:
- Base case – the trivial/easy case where the solution is “obvious”
- Recursive case – the “magic” part where we split the problem up, do a little computation, and then call the function on the subparts
Stack for Recursion
We can recall the Stack data structure:
- a list of items
- push an item onto the stack
- pop an item off of the stack
- “Last In First Out”
The four properties above can perfectly realize the process of recursion.
When computers execute a programming language, they provide a context containing all the variables (and other names) currently in scope. When a function gets called, that context is saved and a new context for the function is “pushed” on top of the old context. This is the (system) call stack and the contexts are stack frames. Each stack frame has entries for all the variables (and functions) defined in the called function.
Python
def sum(k):
if (k <= 1):
// base case
return(1)
else:
// recursive case
return(k + sum(k - 1))
Suppose we want to execute sum(3):
When we execute sum(3), a stack frame is saved and a new stack frame for the function will be "pushed" on the top of stack, the top of system stack is exactly the base, the illustration is as followed:

When the base case has been executed, the top stack frame will be popped off the system stack:
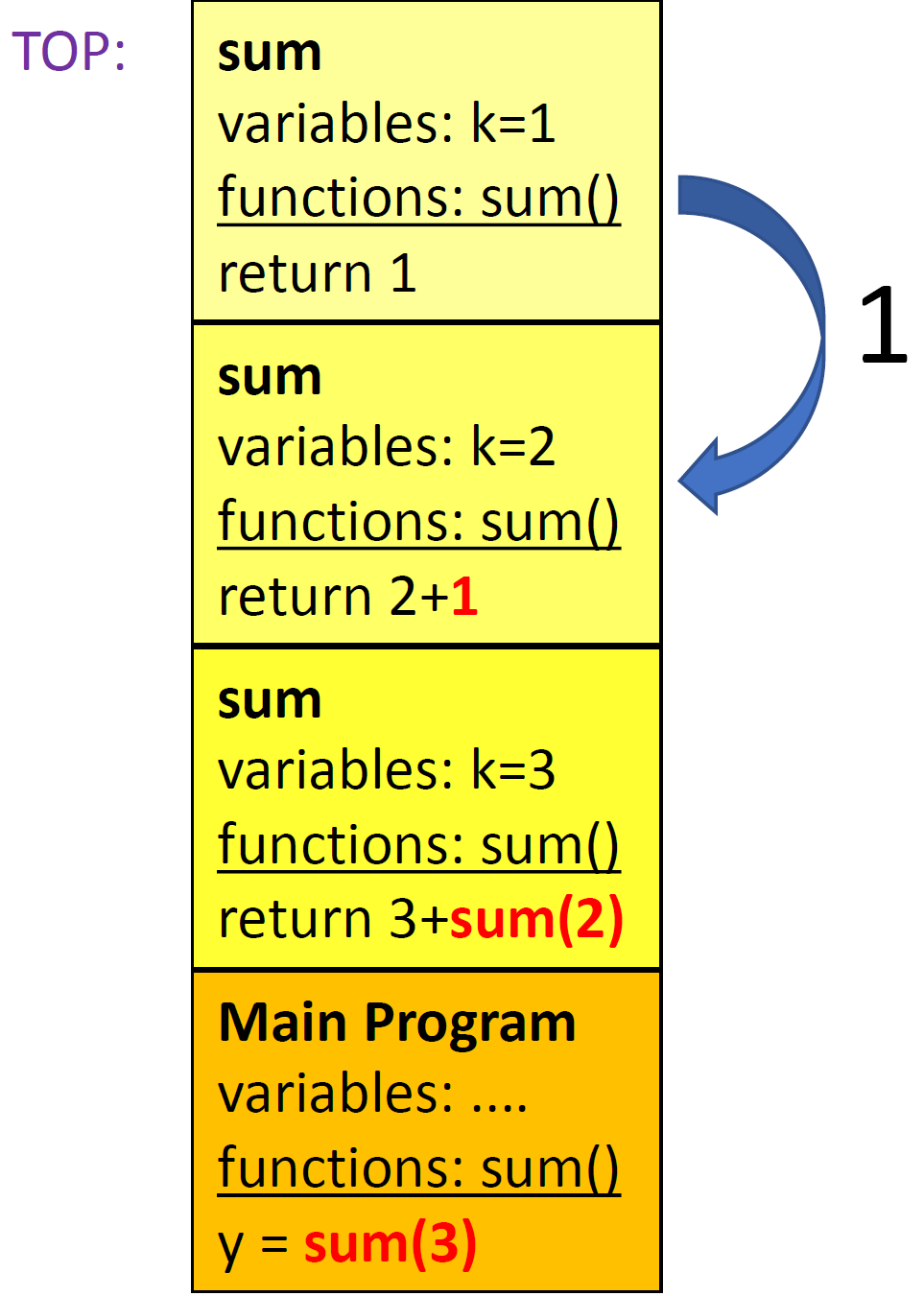
Following this, the next top stack frame will also be popped:

As the process goes, the computer will finally execute the original program and return the correct answer:

Converting Recursive to Iterative Approach
Consider our recursive sum example mentioned above:
Recursive:
def sum(k):
if (k <= 1):
// base case
return(1)
else:
// recursive case
return(k + sum(k - 1))
We can clearly see that the last operation that sum does is to call itself recursively. For recursive implementations like sum, we call them "tail-recursion".
Any recursive solution to a problem has an iterative alternative and vice versa. This principle holds true in tail-recursive operations as well. Recursive implementations realize elegance on coding styles when being done correctly. However, they suffer from one possible problem: stack overflow. The phenomenon of stack overflow occurs when there are too many recursive calls, which fill up the program stack. For the sum function above, the number of recursive calls is exactly equal to k, even though stack overflow will not happen in this scenario, but we may encounter this problem for large numbers.
How can we convert recursion to iteration? In fact, from the recursive implementation, we can conclude that the whole process can be described as ''start with 0, increment the final result by k for every positive k", which shows that a loop can be used for this purpose. The conversion from recursion to iteration is as followed:
Iterative:
def sum(k):
res = 0
while k > 0:
res += k
k--
return res
From the code above we can readily see that we have excellently avoided stack overflow by converting recursive function to iterative one, and that is the power of iteration.
It is worth emphasizing that iteration is not only an alternative for recursion but also an important design technique by itself. In real life, both recursion and iteration play an important role in problem solving.
With this article at OpenGenus, you must have the complete idea of which Data Structure is used for Recursion.
