Stack

Reading time: 20 minutes

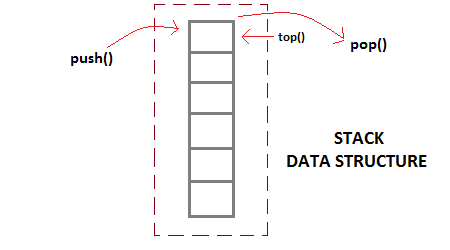
Basic Operations

• Stack - Instantiate the Stack Class

Just instantiate an empty stack object.

Stack() {
  numberOfElements = 0;
}

• push - Add the new element to the stack

If the number of elements pushed on stack are greater than the maximum size of the stack, we have a “Stack Overflow”. Otherwise, we can add a new element to the stack.

void push(int element) {
  if (numberOfElements >= MAX_STACK_SIZE) {
    cout << "Error: Stack Overflow";
  } else {
    container[numberOfElements] = element;
    numberOfElements++;
  }
}

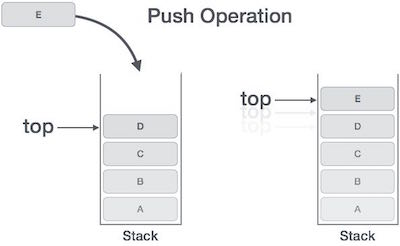
• pop- Remove the last element placed on the stack

If the stack doesn’t have any element (empty), we can’t pop. Otherwise, we just decrease the numberOfElements value.

Note: you can see that we don’t remove the element. It’s not necessary, because top method will always know the element in the top of the stack. And if we add another element to stack, we’ll just reassign the value in that position.

int pop() {
  if (isEmpty()) {
    cout << "Error: No element to pop";
  } else {
    numberOfElements--;
    return container[numberOfElements];
  }
}

• top → Returns the last element placed on the stack

int top() {
  return container[numberOfElements-1];
}

• isFull − check if stack is full.

bool isfull() {
   if(top == MAXSIZE)
      return true;
   else
      return false;
}

• isEmpty - Returns if the stack is empty or not

Verify if there are any element in the stack. Returns true if the stack is empty, and false otherwise.

bool isEmpty() {
  return numberOfElements == 0;
}

• peek − get the top data element of the stack, without removing it.

int peek() {
   return stack[top];
}

Stack Errors

Two things can go wrong with stacks:

• Underflow: An attempt was made to pop an empty stack. Just like with any container class, it doesn't make sense to remove something from an empty collection. Stack underflow is a common error - calls to isEmpty should be used to guard against it. Often times an empty stack is a sign that some part (or all) of a computation is completed.

• Overflow: An attempt was made to push an item onto a full stack. Just like with any container class, we can only add items to a collection if there is enough available memory to store the collection. Some implementations of stacks specify a particular finite size. Others may attempt to emulate infinite stacks (of course, we know that everything in the real world is finite) and only result in stack overflow errors when the computer runs out of memory. Stack overflow is probably most commonly due to recursion that has "gone too far."

Implementation of stack as array

A (bounded) stack can be easily implemented using an array. The first element of the stack (i.e. bottom-most element,) is stored at 0th index in the array (assuming a zero based indexing). The second element will be stored at index 1 and so on. We also maintain a variable top to keep track of the size of the stack by recording the number of items pushed so far. It points to a location in the array where the next element is to be inserted. Thus, the stack itself can be effectively implemented as a 3 element structure.

Complexity

For all the standard stack operations (push, pop, isEmpty, size), the worst-case run-time complexity can be O(1).

Advantages of using Stack

There are many situations where a stack can be useful, a few implementations of it’s use could be found in:

• Backtracking features - This could be an undo feature in a text editing application or to a previous choice point in a game. The stack simply allows us to pop the previous item from it’s data structure.

• Recursive algorithms - When recursing we sometimes need to push temporary data onto a stack, popping the data as we back track through the stages of our algorithm.
  Example:

#include <iostream>
#include <stack>
#include <string>
using namespace std;

// Reverse a string using stack container in C++
// Note that the string is passed by reference
void reverse(string &str)
{
	// create an empty stack
	stack<int> stk;

	// Push each character in the string to the stack
	for (char ch: str) {
		stk.push(ch);
	}

	// pop all characters from the stack and
	// put them back to the input string
	for (int i = 0; i < str.length(); i++) {
		str[i] = stk.top();
		stk.pop();
	}
}

// main function
int main()
{
	string str = "Reverse me";

	reverse(str);
	cout << str;

	return 0;
}

OUTPUT:

em esreveR