Area of Polygon: Shoelace formula

Given Co-ordinates of vertices of polygon, Area of Polygon can be calculated using Shoelace formula described by Mathematician and Physicist Carl Friedrich Gauss where polygon vertices are described by their Cartesian coordinates in the Cartesian plane. This takes O(N) multiplications to calculate the area where N is the number of vertices.

Different Approaches

There are various methods to calculate Area of Polygon, Following are some of the ways :

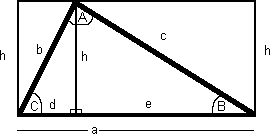
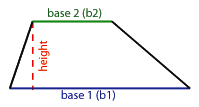
1. Finding Area of Regular Polygon using their Apothems

   1.1 Area = 1/2 * Perimeter * Apothem
   Perimeter = sum of length of all sides.
   Apothem = a segment that joins the polygon's center to the midpoint of any side that is perpendicular to that side

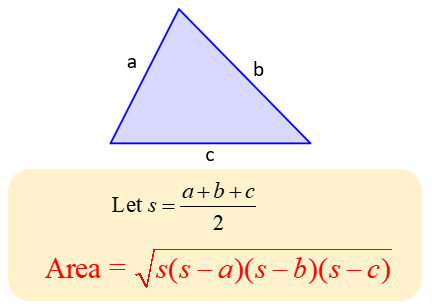
2. Finding Area of known Basic Regular Polygon :

   1. Area of Regular Triangle :
      
      
      
      1.1 Area = 1/2 * Base * Height
      1.2 Area = (a * b * sin(C)) / 2
      1.3 Area = (a2 * sin(B) * sin(C)) / (2 * sin(B + C))
      1.4 Using Heron's Formula
      
      
      
      1.5 Area of Equilateral Triangle = (sqrt(3)/4)(aa)

      2. Area of Square :
         2.1 Area = (side)*(side)
         
         
         

      3. Area of Rectangle :
         3.1 Area = length * breadth
         
         
         

      4. Area of Trapezoid :
         4.1 Area = [(Base-1 + Base-2) x height]/2.
         
         
         

Formula

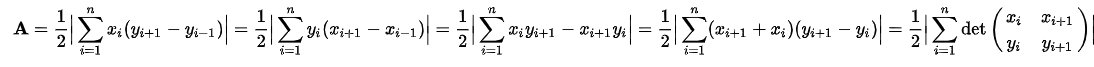
where x is the x-th coordinate of vertice, similarly y is the y-th coordinate of vertice. Indexing of vertices starts from 1,2,3.....n. det is the determinant of successive cross-multiplication of coordinate vertices of polygon.

From above algorithm-formula the computer have to calculate two different sums that could potentially lead to very high numbers, and these numbers could generate an overflow error if they reach the maximum capacity of an double-value. Hence,
The Shoelace formula can be rewritten as follows:

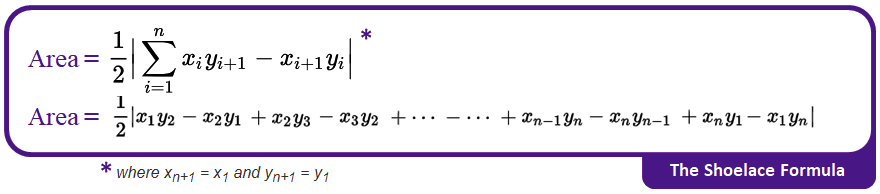
Algorithm

This algorithm consists of rigorous cross-multiplication between corresponding coordinate pairs of the different vertices of a polygon to find the magnitude of area enclosed.

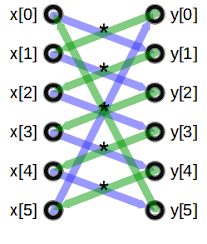
step 1 : List down all the coordinates of vertices of Polygon and note the x and y coordinates in two separate columns in the table having same entry of coordinates in first and last row of table.
step 2 : Calculate the sum of multiplying each x coordinate with the y coordinate in the row below (wrapping back to the first line when you reach the bottom of the table).
step 3 : Calculate the sum of multiplying each y coordinate with the x coordinate in the row below (wrapping back to the first line when you reach the bottom of the table).
step 4 : Subtract the second sum from the first sum, get the Absolute value Difference.
step 5 : Divide the resulting Absolute Difference value by 2 to get the magnitude of Area of the Polygon.
step 6 : Exit.

Example

Let the vertices of polygon be (1, 2), (3, 4), and (5, 7).

step 1 : According to Shoelace Algorithm arrange the given coordinates in tabular form.

Vertices in Tabular Form as follows :

  1    2
  3    4
  5    7
  1    2  [written twice]

step 2: Calculating the sum of multiplying each x coordinate with the y coordinate in the row below,

  1  \  2
  3  \  4
  5  \  7
  1     2
 i.e : 1*4 + 3*7 + 5*7 = 60
 i.e : sum-1 = 60

step 3: Calculating the sum of multiplying each y coordinate with the x coordinate in the row below,

  1  /  2
  3  /  4
  5  /  7
  1     2
 i.e : 2*3 + 4*5 + 7*1 = 33
 i.e : sum-2 = 33

step 4 :

 absolute(sum-1 - sum-2) = |60 - 33|
                         = 27

step 5 :

 Area of Polygon = 1/2 * (absolute(sum-1 - sum-2))
                 = 1/2 * (27)
                 = 13.5

 Area of Polygon is 13.5 square units.

Implementation

        #include <iostream>
        class AreaOfPolygon
        {
        public:
            AreaOfPolygon(int numberOfVertices, double *x, double *y) : numberOfVertices_(numberOfVertices), X(x), Y(y) {}

            double calculateArea();

        private:
            int numberOfVertices_;
            double* X;
            double* Y;

        };

        double AreaOfPolygon::calculateArea()
        {
            //dynamic allocating array to store coordinates of vertices of polygon.
            X = new double[numberOfVertices_];
            Y = new double[numberOfVertices_];

            std::cout << "\nEnter the Coordinates of Vertices of Polygon. ";
            for (int i = 0; i < numberOfVertices_; i++)
            {
                std::cout << "\nEnter X[" << i + 1 << "]-Coordinate : ";
                std::cin >> X[i];
                std::cout << "\nEnter Y[" << i + 1 << "]-Coordinate : ";
                std::cin >> Y[i];
            }

            // Initialze area
            double areaOfPolygon = 0.0;

            // Implementing shoelace formula
            int j = numberOfVertices_ - 1;
            for (int i = 0; i < numberOfVertices_; i++)
            {
                areaOfPolygon += (X[j] + X[i]) * (Y[j] - Y[i]);
                j = i;  // j is referring to previous vertex to i
            }

            return abs(areaOfPolygon / 2.0);

        }

        int main()
        {
            int tnumberOfVertices;
            std::cout << "\nEnter the Number of Vertices of Polygon : ";
            std::cin >> tnumberOfVertices;
            AreaOfPolygon aArea(tnumberOfVertices, NULL, NULL);
            std::cout << "\nArea of Polygon : " << aArea.calculateArea() << " square units.";
        } 
 

Complexity

The time and space complexity of Shoelace Algorithm is :

• Worst case time complexity: Θ(n)
• Average case time complexity: Θ(n)
• Best case time complexity: Θ(n)
• Space complexity: Θ(1)

where n is the Number of Vertices present in Polygon. The value of Complexity depends on the number of cross-multiplication of corresponding coordinates done of vertices of Polygon, which inturn depends on number of vertices polygon is containing, hence time complexity of algorithm is directly proportional to n.