In this problem, we have to formulate an algorithm to find the minimum number of characters to be deleted to make the string a palindrome. This can be solved using the Dynamic Programming approach for longest palindromic subsequence in O(N^2) time.

Examples

Input: 'adbcbea'
Output: 2
As removing 'd' and 'e' will make this string a palindrome string.
Input: 'bbbab'
Output: 1
As removing 'a' will make this string a palindrome string.

Solution

To solve this problem we will use the concept of longest palindromic subsequence. Longest palindromic subsequence is a string is the longest subsequence which is a palindrome. For example in the string 'aabcabc' the longest palindromic subsequence is 'abab'.

So in order to find out the longest palindromic subsequence we will use the following algorithm.

Algorithm-LPS(s):

1. n = s.Length
2. Create M[n][n] matrix
3. for l = 0 to n
    4. for x = 0, y = x+l to x < n and y < n
        5. if l == 0
            6. M[x][y] = 1
        7. else if l == 1
            8. if s[x] == s[y]
                9. M[x][y] = 2
            10. else
                11. M[x][y] = 1
        12. else
            13. if s[x] == s[y]
                14. M[x][y] = 2 + M[x+1][y-1]
            15. else
                16. M[x][y] = max(M[x][y-1], M[x+1][y])
17. return M[0][n-1]

This algorithm returns the length of the longest palindromic subsequence.
Now the minimum number of character to be deleted in order to make this string palindrome is the difference of value returned by the algorithm and the length of the actual string.

The time complexity of this algorithm is O(n^2).

Explanation

The LPS algorithm is based on the dynamic programming approach. In this we create a matrix to store lengths of palindromic subsequences beginning from the first diagonal M[0][0] to M[n][n].

Lets take input string = 'abbcb'.
Now we will follow the steps of the above LPS algorithm.

• Setting n = 5(length of the input string).

• Creating a 2D array M.
  

• Now we will start filling the values in the array.
  for l = 0
  The diagonal values of the matrix from M[0][0] to M[4][4] will be = 1 as l = 0.
  (It means that the subsequence is of length 1 and any string of length 1 is already a palindrome)
  
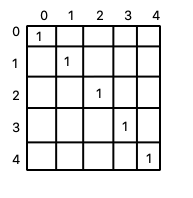
  for l = 1
  if the character at position x and y in the string is same M[x][y] will be = 2 else it will be = 1.
  (It means that there are two characters and we are checking that whether they are same or not, if they are same that means we have a palindromic subsequence of length 2)
  So after repeating this process the array will be.
  
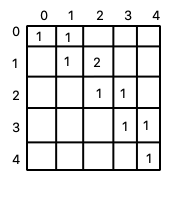
  for l = 2 & 3
  Again we will check the condition according the algorithm and if s[x] == s[y] then M[x][y] = 2 M[x+1][y] else M = max(M[x][y-1], M[x+1][y]).
  (Now finally for subsequences of length more than 2 we need to check if they are palindrome of not to check this we recursively call the same algorithm to calculate the values based on our previous results)
  So finally our matrix will contain the following values.
  

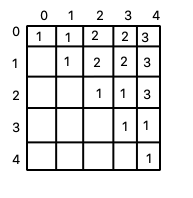
• Now the value of M[0][n-1] is = 3 and length of the string is 5, so our answer is 1.

Implementation (Java):

public class Main {

    static int longestPalindromicSubsequence(String s){
        int n = s.length();
        int[][] dp = new int[n][n];
        for(int l = 0; l < n; l++){
            for(int x = 0, y = x+l; x < n && y < n; x++,y++){
                if(l == 0){
                    dp[x][y] = 1;
                }else if(l == 1){
                    dp[x][y] = s.charAt(x) == s.charAt(y) ? 2 : 1;
                }else{
                    dp[x][y] = s.charAt(x) == s.charAt(y) ? 2 + dp[x+1][y-1] : Math.max(dp[x][y-1], dp[x+1][y]);
                }
            }
        }
        return dp[0][n-1];
    }

    public static void main(String[] args) {
	    String input = "aebcbda";
	    System.out.println(input.length() - longestPalindromicSubsequence(input));
    }
}

Output:

2

With this article at OpenGenus, you must have a complete idea of finding the minimum number of characters to be deleted to make the string a palindrome. Enjoy.