
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes
For numbers from 1 to given n, we have to find the division of the elements into two groups having minimum absolute sum difference. We will explore two techniques:
- Brute force which will take O(2^N) time complexity
- Greedy algorithm which will take O(N) time complexity
Hence, we have reduced an exponential time complexity O(2^N) to a linear time complexity O(N).
Naive Approach O(2^N)
A naive approach would be to generate all subsets of the array of length N and calculating the difference for each of the two subsets in them. Since generating all subsets takes exponential time, this approach is very inefficient.
The steps involved are:
- Generate all subsets of the array and their corresponding complements.
- Calculate the sum of all the elements over the two subsets.
- Compute the absolute sum difference between the two subsets.
- Update the minimum value of the absolute difference.
Pseudocode:
Input: Set[], set_size
1. Get the size of power set
powet_set_size = pow(2, set_size)
min_sum = INT_MAX
2 Loop for counter from 0 to pow_set_size
(a) Loop for i = 0 to set_size
(i) Initialize temp_sum to 0
(ii) If ith bit in counter is set
Print ith element from set for this subset
Update temp_sum by summing with ith element and taking difference with complement sum
(iii) Set min_sum to min(min_sum, temp_sum)
(b) Print seperator for subsets i.e., newline
Greedy Algorithm O(N)
We can divide numbers from 1 to n into two groups such that their absolute sum difference is always 1 or 0. So the absolute difference is atmost 1.
We maintain two counters a and b, both of them initialized to 0 and one temporary variable initialized to half of the sum of the elements.
- Run a loop from n to 1.
- If the element does not exceed sum, insert it into Group 1, increment a by the element and decrement sum by the element.
- Else, insert the element into Group 2.
Implementation
#include <bits/stdc++.h>
using namespace std;
int main()
{
//Obtaining bound of n
int n;
cin >> n;
//Setting half sum value
int sum = (n*(n+1)/2)/2;
//Initializing counter variable
int a = 0, b = 0;
//Maintaining two groups
vector<int> group1, group2;
//Running loop from n to 1
for(int i=n;i>=1;i--){
if(sum-i>=0){
group1.push_back(i);
sum -= i;
a += i;
}else{
group2.push_back(i);
b += i;
}
}
//Printing minimum sum difference
cout << "Minimum difference: " << abs(a-b) << endl;
//Printing the elements of the two groups
cout << "Size of Group 1: " << group1.size() << endl;
for(int i=0;i<group1.size();i++){
cout << group1[i] << " ";
}
cout << endl;
cout << "Size of Group 2: " << group2.size() << endl;
for(int i=0;i<group2.size();i++){
cout << group2[i] << " ";
}
return 0;
}
Examples
//Console input
3
//Console output
Minimum difference: 0
Size of Group 1: 1
3
Size of Group 2: 2
2 1
Here is the state of the two groups for all iterations:

- Here sum is initialized to 3. Since sum - 3 is 0, 3 is inserted into Group 1. For each subsequent element, sum - i is less than 0, so it is inserted into Group 2.
//Console input
6
//Console output
Minimum difference: 1
Size of Group 1: 2
6 4
Size of Group 2: 4
5 3 2 1
Here is the state of the two groups for all iterations:
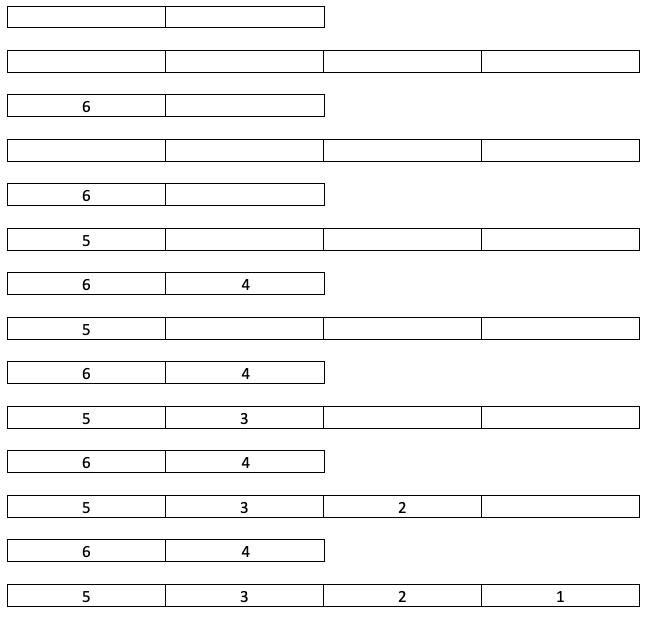
- Here sum is initialized to 10. Since sum - 6 is 4, 6 is inserted into Group 1. Since sum - 5 is less than 0, it is inserted into Group 2. Since sum - 4 is 0, it is inserted into Group 1. For each subsequent element, sum - i is less than 0, so it is inserted into Group 2.
Complexity
The time complexity of this algorithm is O(N), as we loop from N to 1.
