Dynamic Stack

Dynamic Stack, just like Dynamic Array, is a stack data structure whose the length or capacity (maximum number of elements that can be stored) increases or decreases in real time based on the operations (like insertion or deletion) performed on it.

Stack is one of the most popular used data structure which has multiple applications in real life. So we must be familiar with its structure and implementation, so that we can use stack in our program with ease.

We know that stack could be implemented using array and such stack is known as static stack but since we are using array to implement it we cannot insert elements more than the size of array, it will show memory overflow because the size of array is fixed. To overcome this drawback i.e to make stack dynamic we implement stack using linkedlist and such stack is known as dynamic stack and in this section we are going to learn dynamic stack.

Since we are using linkedlist to implement stack, lets get a brief idea about structure of Linkedlist so that we can use it with more ease.
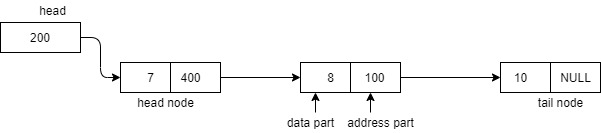
Linkedlist consists of consecutive linked nodes where each node consists of two parts data part and address part, data part stores the value and address part contains the address of next node. There is a pointer called head which stores the address of first node and the address part of last node is set to null since it does not point to any node.

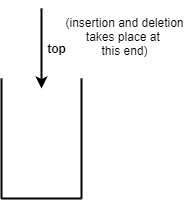
Stack has a container like structure with one open end known as top. Since stack is a ordered list so we can say it is a collection where insertion and deletion are performed at one end(top) only. It always follows the LIFO (Last in First Out) Principle for the insertion and deletion of elements. It's structure look like this-

Since we are implementing stack using linkedlist so we have to store data in form of nodes and follow the all rules of stack i.e LIFO principle. we know that we can perform operation only at the one end of stack, so while implementing it using linkedlist we can take this end either a head node or a tail node. But to perform an operation at the last node we need to traverse the whole linkedlist which results in O(n) time complexity and if we perform operation at first node it results in O(1) time complexity and since we are implementing stack it should be O(1) thats why we choose to perform all the operations at head node. head in linkedlist is termed as top in stack.

Now let us see all the operations on stack using linkedlist one by one , first by code and then by example.

1. push() : We use this method to insert element in stack.
code:

class Node
{
    int data;
    Node next;
    public Node(int data) 
    {
        this.data = data;
        this.next = null;
    }
    Node top = null;     //top is set to null initially, i.e top is not pointing to any node
    void push(int data)
    {
        Node newnode =new Node(data);     // new node is created and data part is set to  "data".
        newnode.next = top;                // newnode will point to previous node, which                                        //top was pointing before
        top = newnode;                   //now top will point to newnode 
        return;
    }

Time complexity: O(1)
Example
Suppose we have to perform operations push(2), push(5), push(7).

• in starting stack was empty and top is pointing to null.
  
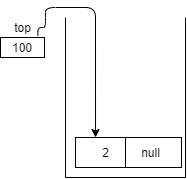
• To insert 2 we will first create a new node and set its data part as 5, lets suppose new node memory address is 100. since we are doing operation at the head end so top should now point to newly created node (i.e address 100) and the address part of node is set to null.
  
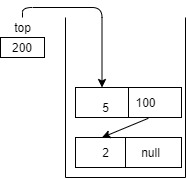
• To insert 5 in the stack we again create a new node, data part is set to 5 and lets suppose new node memory address is 200 now since this new node should point to previous node and top should now point to new node, we will copy the address contained in top to address part of new node and set top pointing to memory address of new node.
  
• And similarly 7 is inserted (lets suppose new node memory address is 300).
  
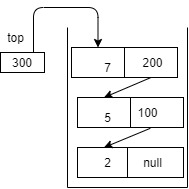
  In this linkedlist implementation of stack we don't need to check if memory overflow is happening while inserting data in stack, because we have not fixed the size of stack, we are creating node dynamically based on demand at runtime, so no issue of overflow arises.

2. pop() : We use this method to delete element from the stack.
code:

void pop()
    {
        if(top == null)
        {
            System.out.println("underflow");
        }
        else
        {
            System.out.println("popped element is :"+ top.data);
            top = top.next;
        }
        return;
    }

Time complexity: O(1)
Example:

Suppose we have to perform pop() operations on the following stack.

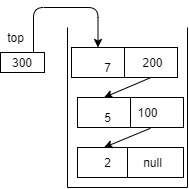
• On pop(), node containing 7 will be deleted and top now will point to next node i.e node containing data 5. So top will point to address 200. So after the first pop() operation, stack will look like-

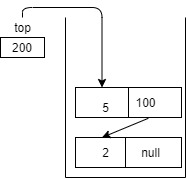
3. display() : This method is used to print the elements of stack.
For this we have to traverse stack from top to bottom i.e we have to traverse linkedlist from head till node becomes null. For this we take another pointer lets say 'temp' which initially point to same address pointed by top pointer. Now we will traverse through linked list using this temp pointer.

code:

void display()
{
    Node temp = top;
    if(temp == null) {
        System.out.println("nothing to display, stack is empty");
        // underflow condition
    }
    else
    {
        while(temp != null)
        {
            System.out.print(temp.data+",");
            temp = temp.next;
        }
    }
    return
}

Time complexity: O(n)
Example:

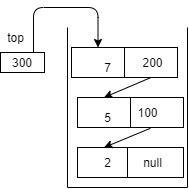
for the above stack output is : 7,5,2

4. peek(): This method gives the element present on top of the stack.
code

void peek()
{
    if(top == null) 
    {
        System.out.println("stack is empty");
        //stack underflow
    }
    else
    {
       System.out.println(top.data); 
    }
    return;
}

Time complexity: O(1)
Example:
for the stack:

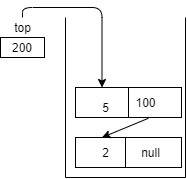
output is : 5

5. isEmpty() : It tells if the stack is empty or there is some element present in stack.
   code

void isEmpty()
{
    if(top == null)
        System.out.println("stack is empty");
    else 
        System.out.println("stack is not empty");
}

Time complexity: O(1)
Example
for stack

output is: stack is empty
for stack
output is: stack is not empty

• To understand this topic in more better way here is a code having all methods altogether.

public class DynamicStack
{
    class Node {
        int data;
        Node next;
        public Node(int data) {
            this.data = data;
            this.next = null;
        }
    }
    Node top = null;
    void push(int x)
    {
        Node newnode = new Node(x);
        newnode.next = top; 
        top = newnode; 
        System.out.println("pushed element is: "+ top.data);
    }

    void display()
    {
        Node temp = top;
        if(temp == null) {
            System.out.println("no data to display");
            // underflow condition
        }
        else
        {
            System.out.println("Elements in stack are:");
            while(temp != null)
            {
                System.out.println(temp.data);
                temp = temp.next;
            }
        }
    }

    void peek()
    {
        if(top == null) {
            System.out.println("stack is empty");
            //stack underflow
        }
        else
        {
            System.out.println("top element is : " + top.data);
        }

    }

    void pop()
    {
        if(top == null)
        {
            System.out.println("underflow");
        }
        else
        {
            System.out.println("popped element is :"+ top.data);
            top = top.next;
        }
        return;
    }
    void isEmpty()
    {
        if(top == null)
        System.out.println("stack is empty");
        else 
        System.out.println("stack is not empty");
    }
    public static void main(String[] args) {
        DynamicStack stack = new DynamicStack();
        stack.push(2);
        stack.push(5);
        stack.push(7);
        stack.display();
        stack.pop();
        stack.peek();
        stack.isEmpty();
        stack.pop();
        stack.pop();
        stack.display();
        stack.isEmpty();
        stack.push(60);
        stack.push(78);
        stack.push(110);
        stack.push(208);
        stack.peek();
        stack.isEmpty();
        stack.display();

    }
}

Output:

pushed element is: 2
pushed element is: 5
pushed element is: 7
Elements in stack are:
7
5
2
popped element is :7
top element is : 5
stack is not empty
popped element is :5
popped element is :2
no data to display
stack is empty
pushed element is: 60
pushed element is: 78
pushed element is: 110
pushed element is: 208
top element is : 208
stack is not empty
Elements in stack are:
208
110
78
60