In this article, we will understand the difference between two key data structures namely Fenwick Tree/ Binary Indexed Tree (BIT) and Segment Tree. We solve the problem "Sum Query Mutable" to explore the differences.

Fenwick Tree(BIT) vs Segment Tree

The differences between Fenwick Tree(BIT) and Segment Tree are:

1. Fenwick tree can compute only sums from 1..x we need to subtract sum(1,y-1)accordingly to obtain answer where as segment tree computes between x,y range and manipulation is not required.
2. Since BIT computes from 1...x , we cannot use fenwick trees for other purposes like max or other functions which are not invertible.
3. Fenwick trees are online data structures , which means that even if you add elements to the end it will remain same.
4. Even though memory for both is O(n) but Fenwick tree requires lesser memory than Segment tree as worst case is 4n and BIT it is n.
5. BIT are easier to code than segment tree.Recursion is not required in fenwick trees and few operations are required to perform thus contributing to the speed , segment trees can also be modified similarly but requires extra effort.
6. Segment Trees can be used to solve more problems than fenwick tree.
7. Preprocessing of segment trees is O(N) whereas of fenwick tree is O(NLogN) because of the update function involved in n complexity for loop.

Problem

Given an integer array nums, handle multiple queries of the following types:

1. Update the value of an element in nums.

2. Calculate the sum of the elements of nums between indices left and right inclusive where left <= right.

Brute Force

1. Array of elements .
2. Update in O(1) time.
3. Then find the sum across the given range which would take O(n).
4. With q queries , this could have worst case O(q*n)

Segment tree

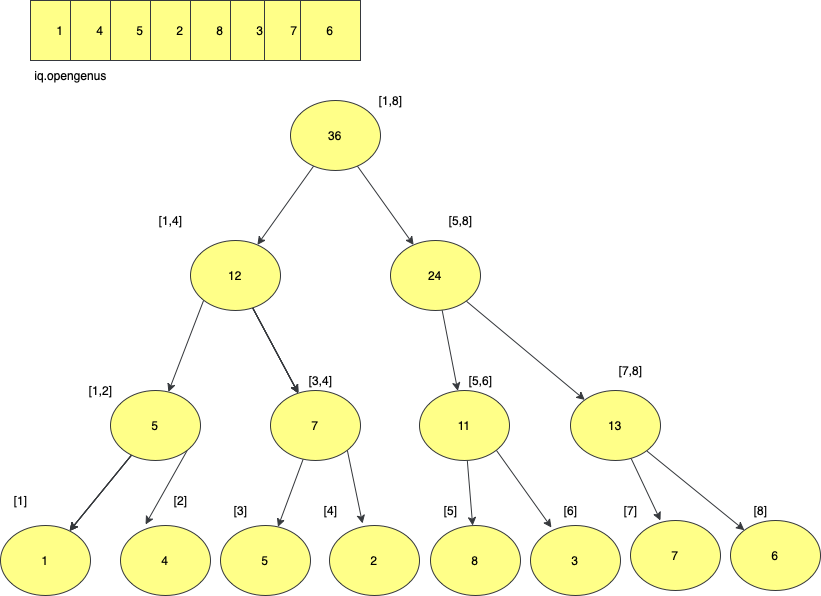
Idea -

In brute force approach we updated the value in constant time but when it came to sum updation , it took O(n) time. This could be costly especially if you have many queries . Segment is a type of tree that stores the sums and during updation can update the sum in O(logn) time .

Characteristics of segment tree:

1. Root - Represents sum of all the elements.
2. Leaves - Individual elements of the array.
3. Other nodes - represents sum across a certain range.
4. Each node's left and right child represent sum of ranges [a,b/2] and [b/2+1,c] respectively.
5. And that particular node to would store the sum of range [a,c].
6. Hence the relation that occurs node_value = right_node_value+left_node_value.

If you observe the tree image embedded you can see that at :

• 1st level - 1 node
• 2nd level - 2 nodes
• 3rd level - 4 nodes
• 4th level - 8 nodes ....
  so the sequence would be 1,2,4,8...,n/4,n/2,n.
  Total no of nodes = 1+2+4+8...+n/4+n/2+n which is a form of geometric progression.
  Let x be no of terms,
  Last term = ar^x-1 where a is 1st term and r is common ratio
  so common ratio(r) is 2 and 1st term(a) is 1.

Therefore Last term = 2^x-1.
We know that Last term = n.
n=2^x-1
Applying logn on both sides ,
logn = x-1;
x=logn+1

Thus no of terms(height of tree) = logn+1.
But to find number of nodes we need to find sum of the above G.P.

sum = a(r^(x)-1)/(r-1)
= > (2^(logn+1)-1)/(2-1)
Total no of nodes = > 2^(logn+1)-1

Using property,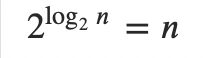

Total no of nodes = 2n-1

But in worst case if the segment tree has odd levels, then the no of nodes can be more and max it can be extended to 4n.

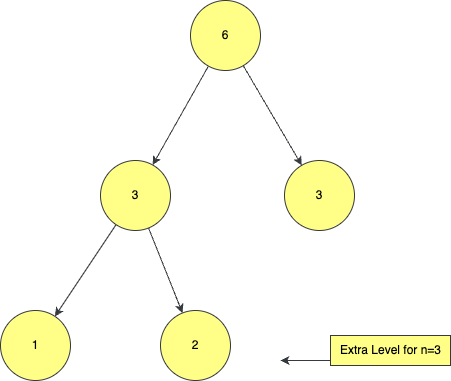
Implementation

Build Operation

 void buildTree(vector<int>& nums, int i, int left, int right){
        if (left == right){
            tree[i] = nums[left]; 
            return;
        }
        int mid = (left+right)/2;
        buildTree(nums, 2*i, left, mid);
        buildTree(nums, 2*i+1, mid+1, right);
        tree[i]=tree[2*i+1]+ tree[2*i];
    }

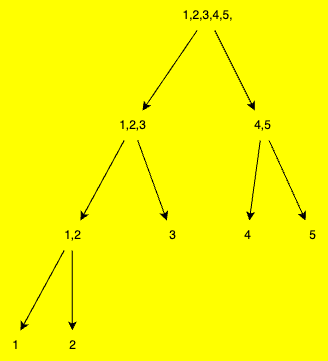
• Here we build tree with left child at 2*i and right child at 2*i+1.
• In case of the lone node we directly add the node and return.
• For the left node - we divide from [left...mid] sum.
• For the right node - we divide from [mid...right] sum.
  -

Update Operation

void updateUtil(int pos, int left, int right, int index, int val) {
        
        if(index <left || index >right) return;
        if(left==right){
            if(left==index)
                tree[pos]=val;
            return;
        }

        int mid=(left+right)/2;
        updateUtil(2*pos,left,mid,index,val); // left child
        updateUtil(2*pos+1,mid+1,right,index,val); // right child
        tree[pos]=tree[2*pos]+tree[2*pos+1];
    }

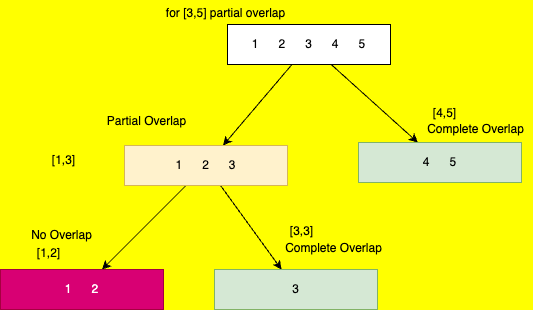
Sum Range Operation

int range(int qlow, int qhigh, int low, int high, int pos){
        if (qlow <= low && qhigh>= high){ // total overlap
            return tree[pos];
        }
        if (qlow > high || qhigh < low) { // no overlap
            return 0;
        }
        // partial overlap
        int mid = low+(high-low)/2;
        return (range(qlow, qhigh, low, mid, 2*pos) + range(qlow, qhigh, mid+1, high, 2*pos+1));
    }

Code

class NumArray {
public:

    vector<int> tree; 
    int n;
    void buildTree(vector<int>& nums, int pos, int left, int right){
        if (left == right){
            tree[pos] = nums[left]; 
            return;
        }
        int mid = (left+right)/2;
        buildTree(nums, 2*pos, left, mid);
        buildTree(nums, 2*pos+1, mid+1, right);
        tree[pos]=tree[2*pos+1]+ tree[2*pos];
    }
     void updateUtil(int pos, int left, int right, int index, int val) {
        
        if(index <left || index >right) return;
        if(left==right){
            if(left==index)
                tree[pos]=val;
            return;
        }

        int mid=(left+right)/2;
        updateUtil(2*pos,left,mid,index,val); // left child
        updateUtil(2*pos+1,mid+1,right,index,val); // right child
        tree[pos]=tree[2*pos]+tree[2*pos+1];
    }

    NumArray(vector<int>& nums) {
        if(nums.size() > 0){
            n = nums.size();
            tree.resize(4*n,0);  
            buildTree(nums, 1, 0, n-1);
    }
    }
    
    void update(int index, int val) {
         if(n==0)return;
        updateUtil(1,0,n-1, index, val);
    }
    int range(int qlow, int qhigh, int low, int high, int pos){
        if (qlow <= low && qhigh>= high){ // total overlap
            return tree[pos];
        }
        if (qlow > high || qhigh < low) { // no overlap
            return 0;
        }
        // partial overlap
        int mid = low+(high-low)/2;
        return (range(qlow, qhigh, low, mid, 2*pos) + range(qlow, qhigh, mid+1, high, 2*pos+1));
    }
    int sumRange(int left, int right) {
        if(n==0)return 0;
        return range(left, right, 0, n-1, 1); 
    }
};

Performance

Time Complexity

• Update - O(logn)
• Build - O(4*n)
• Sum finding -O(logn)
• Worst case time complexity - O(4*n)

Space Complexity

• O(4n) where n is no of elements

Fenwick Tree

Fenwick is also called Binary indexed tree. It is easy to code , with same time complexity and space as the segment tree.We have a bit array which is fenwick tree for us where we store the sum of the elements depending upon Least significant bit mechanism.

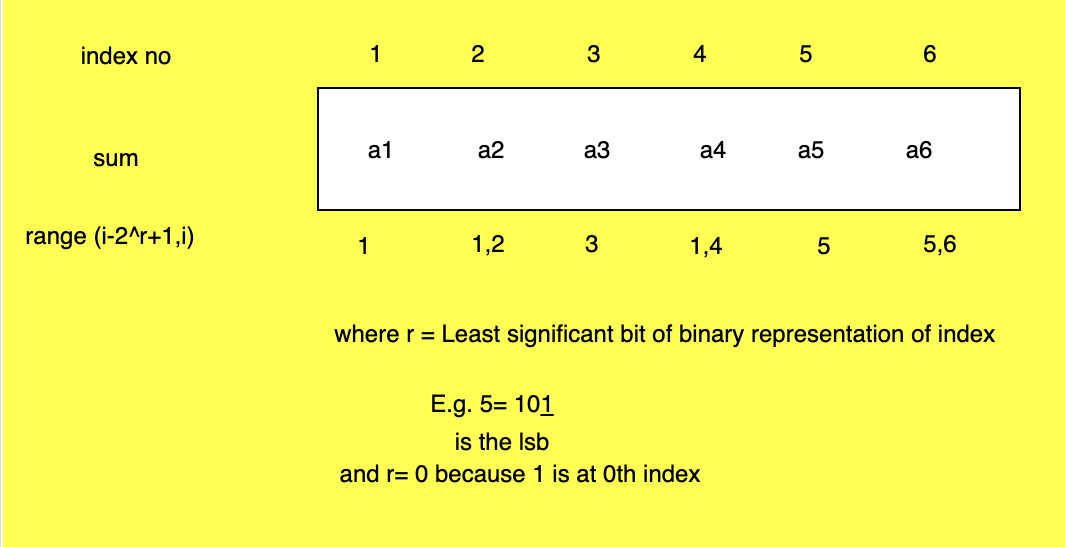
BIT Array :

We have 1-indexed array that stores sum at index according to formula i-2^r+1 to i where r= index of the LSB of the binary representation of i.
Let us refer to example of 5 where the sum has been stored only for 5th index because lsb's index is 0 and 5-2^0+1 = 5 and i = 5.

Implementation

class NumArray {
public:
vector<int> bit,arr;
int n;
    NumArray(vector<int>& nums) {
        arr=nums;
        n=nums.size();
        bit=vector<int>(nums.size()+1);
        for(int i=0;i<nums.size();i++)
          build(i,arr[i]);
    }
    void build(int i, int val) {//update value at index i
       i++;
		while (i <= n) {
			bit[i] += val;
			i += (i & -i); //update for subsequent indexes
		}
    }
    void update(int i, int val) {
        int d = val - arr[i];
		arr[i] = val;
		build(i, d);
    }
    int sum(int i) {
		int sum = 0;
		i++;
		while (i > 0) {
			sum += bit[i];
			i -= (i & -i);//find smaller sums by removing lsb
		}
		return sum;
	}
    
    int sumRange(int left, int right) {
        return sum(right) - sum(left - 1);
    }
};

Updating the value-

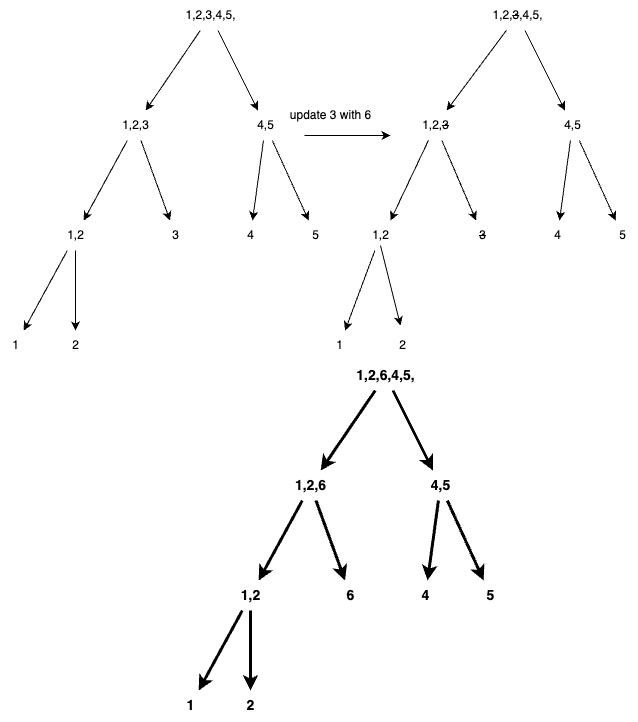
When we update the value at a particular index we know that , subsequent changes will be reflected in further indices too,so we need to update the value after the particular index too.

Therefore given an array , [1,2,3,4,5] and we need to change index=2 valued 2 as 6, i.e [1,6,3,4,5]. So we add least significant bit and add at each place till the end of the bit array.

We make use of this formula - i+=(i&-i) so that we can add Least significant bit till i is equal to size of bit array.

-i ==> ~i+1 where ~i means complement of i (eg i=1010, ~i = 0101 and ~i+1=0110)

when we have i&-i , we get ==> 1010 & 0110 ==> 0010 thus it gets us the least significang bit. Least significant bit refers to set bit at the rightmost index.

Finding sum-

While we increment i with (i&-i) while updating , we decrement while finding sum over a particular range [x,1].
while decrementing we add sum for i-2^r+1 to i where r = lsb index
For e.g.: [7,1] ==> for 7th index :

• at 7: 7,7 since lsb = 0 and i-2^0+1 = 7(7 binary is 111)
• at 6: 5,6 since lsb = 1 and i-2^1+1 = 5(6 binary is 110)
• at 5 : 5,5
• at 4 : 1,4 since lsb = 3 and i-2^2+1 = 1(4 binary is 100)

Thus for sum of range(1,7) we get -- sum(7,7)+sum(5,6)+sum(1,4).

finally for sum of range [l,r] we find sums for (r,1) and (l-1,1) and decrement (l-1,1) from (r,1) sum.

Performance

Time Complexity

• Update -O(logn)
• Build - O(n*logn)
• Sum - O(logn)

Space Complexity

O(n) where n is no of elements

With this article at OpenGenus, you must have a strong idea of Fenwick Tree(BIT) vs Segment Tree.