Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 5 minutes
In this problem, we are given two positive integers M and N. The task is to find the smallest number that has length M (number of digits) and sum of digits as N. We will solve this using a greedy approach in O(M).
Some examples:
For M=3 and N=5, the smallest number is 104.
We can have other numbers like 212 and 230 but these are not the smallest number.
For M=3 and N=15, the smallest number is 159.
Other numbers that satisfy the condition but are not the smallest are:
519 and 663.
Note that Numbers cannot start with leading zeros and 0 < N <= M * 9
We will attack this problem using a greedy approach and solve it in O(M) time complexity.
First I ask the readers to try and solve this problem alone (give 25 minutes ).
Couldn' solve it? No problem you have another task look at the problem and collect as many observations and patterns as you can! can u see the solution now?
I will aproach this problem throw observations
-
1- 600>599 and 2000>1999 We can see that with fixed number of digits (m) numbers with smallest most significant digit are smaller
-
2- 660>559 and 3300>3299 If two numbers have the most significant digits equal the digit second in order determines it's value.
-
3- the minmum value for the most significant digit is 1 why?
While other digits have a minmum value of 0.
These observation are intutive and 1000 being smallest number with M=3 and N=1 as an example.
Based on those observation we make some conclusions didn'u discover them already?
- 1- we should make left most digits as small as possible.
- 2- we can ditribut n(digit sum) on digits and from conclusion(1) we should put them on the right most digits.
How this strategy works?
Let's look at an example
m=4 , n=9 number should look like:
d0 d1 d2 d3
We know that d0 > 0 as the number can't contain leading zeros so we should make d3 as heavy as possible min(9,n-1) (why?) (because it can be maximum 9 or 1 less than N as 1 is the minimum value to be assigned to d0)
We get d4 = 8 and the number is 1008
Harder example
Let m=4 , n=30, the number format will be:
d0 d1 d2 d3
we make d3 as heavy as possible d3 = min(9,n-1).
Now what about d2? following same thinking model it should be as heavy as possible but sum of the remaining digits n= n-d3. why?
d3=min(9,30-1) = 9
d2=min(9,21-1) = 9
d1=min(9,12-1) = 9
last digit gets the remaining sum
d0 = n - (d1 + d2 + d3)
From the above algorithm we can build this code. The pseudocode will be as follows:
short digits[M]; // M digit number
for(long long i = m-1; i>0; i--)
{
digits[i] = min(( 9, n-1);
n-=digits[i];
}
digits[0]=n;
Implementation
Following is the implementation in C++:
// library
#include <bits/stdc++.h>
using namespace std;
int main ()
{
ios_base::sync_with_stdio(false);//these lines
cin.tie(NULL); // allows faster input
int testCases = 5; //number of test cases
while(testCases--)
{
long long m , n; // can this algorithm handle 64 bit input??
short digits[100000]; // to store digits
cin>>m>>n;
for(long long i=m-1;i>0;i--)
{
digits[i]=min((long long)9,n-1); // determine digit value
n-=digits[i]; // decrease sum of remaining digits
}
digits[0]=n; //assign the left most with the remainder
for( long long i=0;i<m;i++)//output
cout<<digits[i];
cout<<endl<<endl<<endl; // to sperate test cases
}
}
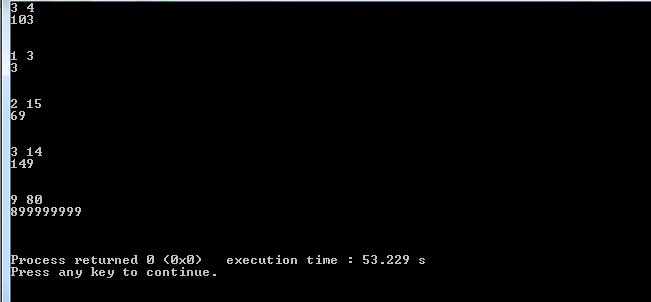
Some input output results
A serious issue arises with this code did u see it?
Memory this code needs at least 1 char (8 bits) of storage for each digit. This arises with huge values of m long long can handle (e.g. m= 10e17 ).
To solve this issue we need to think in reverse a bit. Try and solve it.
Hope you did find last task easy. We store data because we calculate digits we print last first if we could calculat d0 first then d1 we don't have to store it we can print it on the spot.
This code works on reverse (c++ again)
// library
#include <bits/stdc++.h>
using namespace std;
int main ()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int testCases = 5;
while(testCases--)
{
long long m , n;
short temp;
cin>>m>>n;
temp=max((long long)1,n-9*(m-1));
n-=temp;
cout<<temp;
for(long long i=1;i<m;i++)
{
temp=max((long long)0,n-9*(m-i-1));
n-=temp;
cout<<temp;
}
cout<<endl<<endl<<endl;
}
}
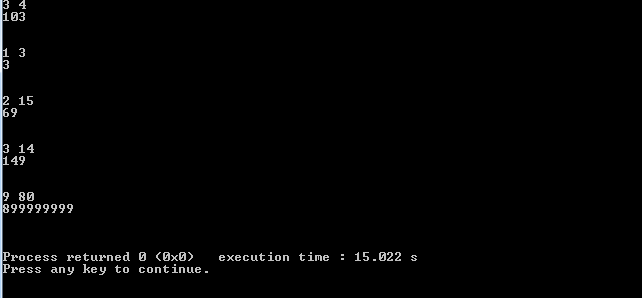
Some outputs:
We can see this code takes much less time obvioulsy both ways run in order of m O(M) but second implementation have much better constant.
Last task for you?
If you have knowlege about dp how would u solve this problem? does it has a greedy property? This should be easy if you could solve it already
Solve it to find the largest number satisfying the conditions.