Bucket in Unordered map in C++ STL

Reading time: 30 minutes | Coding time: 5 minutes

Unordered Map is a data structure that maps key value pairs using Hash Table.
This article is focused on what Buckets mean in Hashing and the function unordered_map::bucket for unordered map container in C++ STL. This function is used to check if 2 elements have the same hash and hence, falls into the same bucket.

The syntax of using it is:

map.bucket(key);

where map is the unordered map and key is the key of the key value pair.

What is a bucket ?

The std::unordered_map has a Bucket Interface in C++. Imagine a hash map, where each element is a pointer to a linked list and the actual data is stored in the linked list. Hence, each element is a bucket and contains several elements. Consider this image to get the idea:

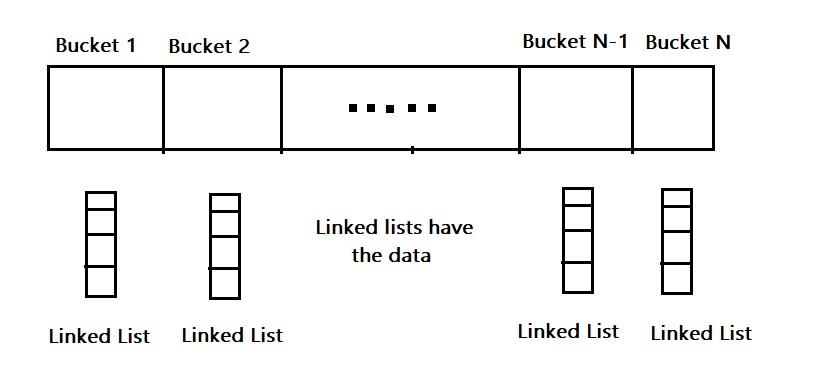
The keys of the unordered_map are stored in buckets. Each key belongs to a particular bucket. It is possible that two keys might be stored in the same bucket and this might be happening due to hash collisions.

Mathematically speaking : two keys (say x1 and x2) are said to have the same hash value if:

h(x1) = h(x2) (that is a collision)
Where h is the Hash Function.

Buckets are a mechanism to manage hash collisions in a Hash map.

The job of a Hash Function is to map potentially infinite keys to a finite number of locations or buckets. So hash collisions are inevitable and this phenomenon is merely an instance of the Pigeonhole Principle.

Pigeon Hole Principle states that if we distribute N items among M objects and M < N, then there will be atleast one object with more than 1 item.

In order to decide which bucket to place an element in, the container applies the hash function, Hash, to the element's key. This returns a value of type:

std::size_t(size_t is an alias of the unsigned integer type)

std::size_t has a much greater range of values then the number of buckets.

So for example size_t has a range from 0 to 4 * 10^9 (4 Billion) but the number of buckets present might be lesser. This is where the Pigeon Hole principle comes into play. So, the unordered_map applies another transformation to the hash value(size_t) to choose a bucket to place the element in.

Now when we search for a value in the unordered_map, the unordered_map can find the hash value of the element we are searching for and then apply the same transformation to the hash value to find out which bucket the element is expected to be present in and then looks for the key in that particular bucket.

So the unordered_map may place elements with the same hash value in the same bucket. Actually it depends on the type of transformation applied to the hash value. The method by which keys are placed in particular buckets can vary from one implementation to the other.

std::unordered_map::bucket

The bucket function returns the bucket number a particular key belongs to.
So 2 or more keys with the same hash value will have the same bucket number as they have the same hash value.

The syntax of using the function is as follows:

map.bucket(key);

where map is the unordered map and key is the key of the key value pair.

Example

Consider this complete example:

// unordered_map :: bucket
#include<iostream>
#include<string>
#include<unordered_map>
int main()
{
	std :: unordered_map < int, std :: string > mp = 
	{
		{1, "I"},
		{2, "Love"},
		{3, "OpenGenus"}
	};
    for(auto z : mp)
	{
		std::cout << "Element[" << z.first << ":" << z.second << "]";
		std::cout << " is in Bucket #" << mp.bucket(z.first) << std :: endl;
	}
	return 0;	
}

Output:

Element[3:OpenGenus] is in Bucket #3
Element[1:I] is in Bucket #1
Element[2:Love] is in Bucket #2

Complexity

• Worst case time complexity : Θ(1)
• Average case time complexity : Θ(1)
• Best case time complexity : Θ(1)

Further Reading

Microsoft docs
CPP Reference