Finding the number of sub matrices having sum divisible by K

Reading time: 30 minutes | Coding time: 10 minutes

You are given a N X N matrix of integral values and you have to find the count of the sub matrices such that the sum of the elements of the sub matrices is divisible by a positive integer k.

We use a Dynamic Programming approach to solve this in O(N^3)

For example if the N X N matrix is :

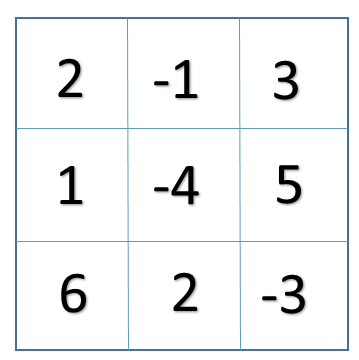
and the value of k=4

The different sub matrices which have sum divisible by k(4 in this case)are:
a). A sub matrix with sum=0

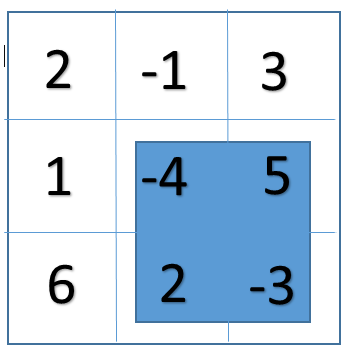
b). A sub matrix with sum=4

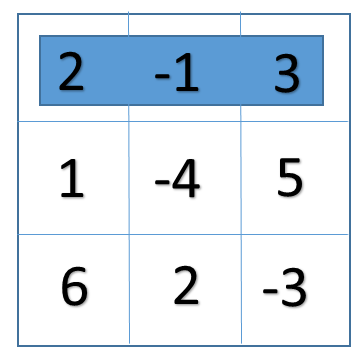
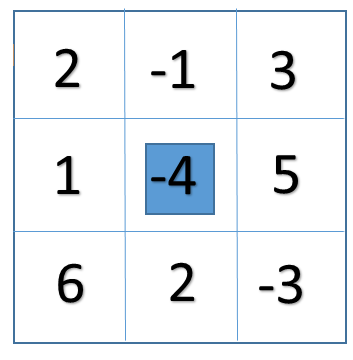
c). A sum matrix with sum=8

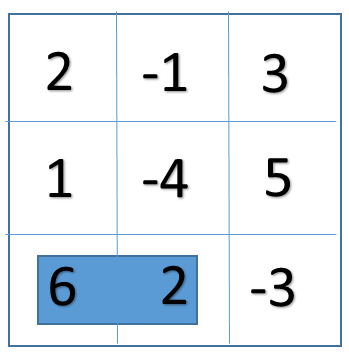
d). A sub matrix with sum=8

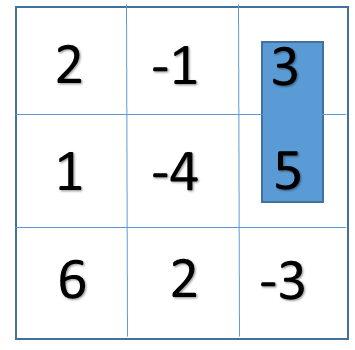
e). A sub matrix with sum=-4

Input format:

We will have to input the value of N for the N X N matrix and the value of k(for checking the divisible sub matrices).The matrix will also be entered by the user.

Output format:

The output will be a non negative value indicating the count of number of sub matrices having sum divisible by k.

Method of Implementation:

We will solve the problem by applying the following approach:

Step 1: One by one we will fix the left and right index for all the possible column in the matrix. For eg: If our N=5 then we will check for index pairs:

[ (0,0) (0,1) (0,2) (0,3) (1,1) (1,2) (1,3) .....(3,3) (3,4) (4,4) ]

Step 2: Now for every left and right index we will calculate the temporary sum[] array.

Step 3: Next we will apply the algorithm mentioned below to count the total number of subarrays having sum divisible by k.

Step 4: So likewise we will get the total number of subarrays (having sum divisible by k) for all the sum[] arrays for every possible left and right column index pair.

Step 5: Adding the result for all the left and right column index pair will give us the count of the number of the rectangular submatrix such that the sum of the elements is divisible by k.

Pseudocode:

1. Consider all the left and right indexes for every column pair.

2. Store the sum of every row within the left and right indexes in sum[].

3. Follow the steps to find the number subarray for sum[] which has sum of elements divisible by k.

4. Create a count[] array where count[i] stores the count of the remainder i after dividing current cumulative sum till any index in sum[].

5. Linearly traverse sum[] and keep on calculating the cumulative sum and find (curr_sum % k) and increment its count in the count[] array.

6. Now linearly traverse the count[] array and if count[i]>1 then we have to find the number of ways we can choose the indices for the subarray and it can be done in (count[i](count[i]-1))/2 ways i.e. result+=(count[i](count[i]-1))/2 .

result+=(count[i]*(count[i]-1))/2 

7. Next we will also have to include the count of the elements whose sum=0 and for that we will do, result += count[0].

result += count[0] // for sum = 0

8. Likewise we will get the result for all the left and right indices of columns and we will report the cumulative result.

Implementation:

#include<bits/stdc++.h>
using namespace std;

#define MAX 100

int NumberOfSubarrayDivSumK(int sum[], int n, int k);

void countOfSubMatrices(int mat[MAX][MAX], int n, int k)
{
	//Initialising the variables
   int AreaMaximum= 0;
   int left,right,i;

   int sum[n];
   int result = 0;
   
   //Considering all the left and right column pair indices
   for(left=0; left<n; left++)
   {
       
   	   for(i=0;i<n;i++)
   	   sum[i]=0;
   	   
   	  //end of the column index
   	   for(right=left; right<n; right++)
   	   {
             //Calculating the cumulative sum
              for(i=0;i<n;i++)
   	   	      {
   	   	        sum[i]=sum[i]+ mat[i][right];
	          }
			 
         result += NumberOfSubarrayDivSumK(sum , n , k);
	   }
   }
  cout<<"The total number of sub matrices divisible by k are: "<<result;
}

int NumberOfSubarrayDivSumK(int sum[], int n, int k)
{
	int count[k];
	int result=0;

	int presentSum=0;
	int LenMax=0;
	int i,j;
	
	//assigning all the values to 0
	for(i=0;i<k;i++)
	{
		count[i]=0;
	}
   
    //calculating the count of all the remainders possible
	for(i=0;i<n;i++)
	{
		presentSum=presentSum+sum[i];
	
		count[((presentSum % k )+ k) % k]++;
    }
    
	for(i=0;i<k;i++)
	{
		//if there are more than one subarrays with same remainder
        if(count[i]>1)
		{
            result += (count[i]*(count[i]-1))/2;
		}
    }
      //including the elements which add up to 0
      result += count[0];
      
    return result;
}
int main()
{
	cout<<"Enter the value for N: "<<endl;
	int N;
	cin>>N;
	cout<<"Enter the value for k : "<<endl;
	int k;
	cin>>k;
	cout<<"Enter your N X N matrix :"<<endl;
	int i,j;
	int mat[MAX][MAX];
	for(i=0;i<N;i++)
	{
		for(j=0;j<N;j++)
		{
			cin>>mat[i][j];
		}
	}
	countOfSubMatrices(mat, N, k);
	return 0;
}

Complexity Analysis:

Time complexity: O(n^3)
Space complexity (Auxillary Space): O(n)

Explaination with an example:

For eg: if for N=3 our matrix is:

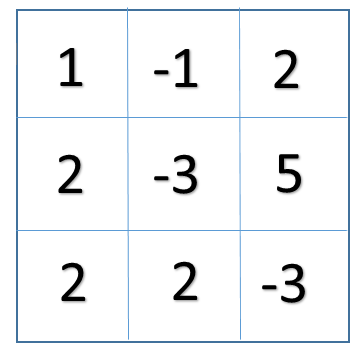
and the value of k=4
then first we consider all the possible pairs of columns: (0, 0) (0, 1) (0,2) (1, 1) (1, 2) (2, 2)
So now will calculate the sum[] which is a temporary array for storing the sum:
eg. for (0, 1) sum[]={0, -1, 4}
Now we will apply the above algorithm to calculate the number of subarrays such that the sum is divisible by k(4 in this case).
So the total number of sub matrices we get is 6. They are:

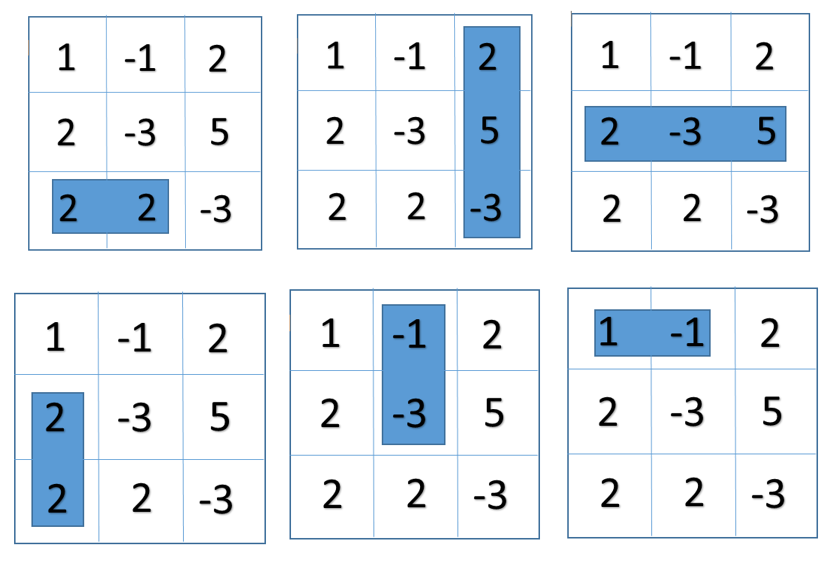
Applications:

The above code can be used to find the count of the number of the rectangular submatrix such that the sum of the elements is divisible by k.

Question

You are given a N X N matrix and you have to find out the number of rectangular submatrix such that the sum of all the elements in that submatrix is divisible by an integer k.

Input:
Enter the value for N: .........
Enter the value for k: .........
Enter your N X N matrix: .........

Output:
The total number of sub matrices divisible by k are: .........