Reading time: 40 minutes

A clique is a subset of vertices of an undirected graph G such that every two distinct vertices in the clique are adjacent; that is, its induced subgraph is complete. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs.

A maximal clique is a clique that cannot be extended by including one more adjacent vertex, that is, a clique which does not exist exclusively within the vertex set of a larger clique. Maximal cliques can be very small. A graph may contain a non-maximal clique with many vertices and a separate clique of size 2 which is maximal. While a maximum (i.e., largest) clique is necessarily maximal, the converse does not hold.

There can be more than one single maximal clique in a non-complete graph (since complete graph is a maximal clique itself). To find a single maximal clique in a graph we use a straightforward greedy algorithm.

Algorithm

In greedy approach of finding a single maximal clique we start with any Starting with an arbitrary clique (for instance, any single vertex or even the empty set), grow the current clique one vertex at a time by looping through the graph's remaining vertices.

For each vertex v that this loop examines, add v to the clique if it is adjacent to every vertex that is already in the clique, and discard v otherwise. The maximal clique can be different if we start with differnet vertex as a graph may have more than one maximal clique.

• Start from an arbitrary vertex
• Given a clique of size, repeat:
  • Add a vertex randomly from the common neighbors of the existing clique
  • If there is no common neighbors, stop and return the clique

The above algorithm runs in linear time in the size of the graph (Θ(n²) edges) because of:

• the ease of finding maximal cliques
• their potential small size

Following is an example graph with 6 vertices and 4 different maximal cliques. On selection of different arbitrary start vertex we may get different maximal clique as output of the algorithm.

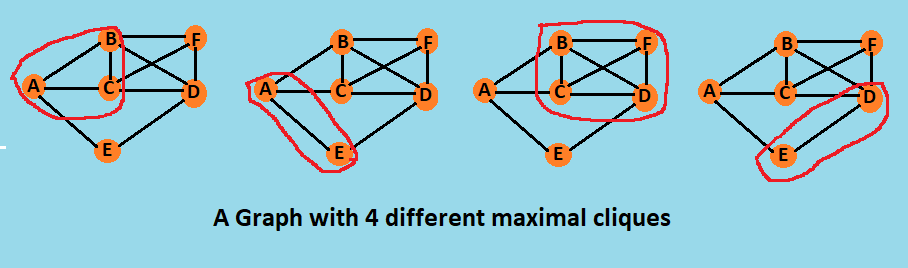
Implementation

Code in Python3

from collections import defaultdict
import random

def find_single_clique(graph):
    clique = []
    vertices = list(graph.keys())
    rand = random.randrange(0, len(vertices), 1)
    clique.append(vertices[rand])
    for v in vertices:
        if v in clique:
            continue
        isNext = True
        for u in clique:
            if u in graph[v]:
                continue
            else:
                isNext = False
                break
        if isNext:
            clique.append(v)

    return sorted(clique)

graph = dict()
graph['A'] = ['B', 'C', 'E']
graph['B'] = ['A', 'C', 'D', 'F']
graph['C'] = ['A', 'B', 'D', 'F']
graph['D'] = ['C', 'E', 'B', 'F']
graph['E'] = ['A', 'D']
graph['F'] = ['B', 'C', 'D']

clique = find_single_clique(graph)
print('A maximal clique in the graph is: ', clique)

Output

A maximal clique in the graph is:  ['B', 'C', 'D', 'F']

Complexity

Time Complexity

• The greedy algorithm takes O(n²) (i.e. O(Edges)) time in the worst case.

Space Complexity

• The greedy algoorithm takes O(n²) auxiliary space in the worst case.

Related articles

References

• lecture doc from yale.edu on greedy algorithm to find single maximal clique.