Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Given two linked lists, where the tail of the second list points to a node in the first list, find the node where both the lists intersect.
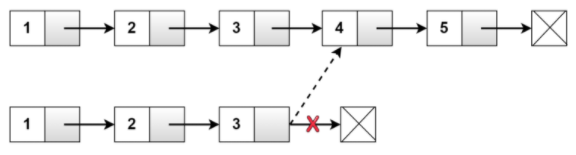
Consider the following example where the tail of second list points to the fourth node of the first list. The code should return 4 as the intersection point.
A simple (naive) solution is to consider each node of the first list and check if it can be reached from the second list. The first node in the first list that is reachable from the second list is the intersection point. The time complexity of this solution is O(m.n) where m represents the total number of elements in the first list and n represents the total number of elements in the second list.
However, the solution is far from optimal. There are many different ways in which the time complexity of this algorithm can be improved.
Idea behind solving this problem
We have explored 4 approaches to find Intersection point of two linked lists:
- Using hash table
- Using Floyd’s Cycle Detection Algorithm
- Using difference in node counts
- Using distance from intersection point
1. Using hash tables
The steps to find Intersection point of two linked lists using Hash tables are:
- Traverse the first list
- Store each node’s address in a hash table.
- Traverse the second list
- While traversing the second list, get the address of the first node present in the hash table.
- If the address matches, that node would be the intersection point.
2. Using Floyd’s Cycle Detection Algorithm
Another approach is to make the first linked list circular by linking its tail to the head. Then the problem reduces to finding a loop in the second linked list.
The idea is to get a pointer to the loop node using Floyd's Cycle Detection Algorithm. Floyd’s Cycle Detection Algorithm, also called the "tortoise and the hare algorithm" is a pointer algorithm that uses only two pointers, moving through the sequence at different speeds.
The steps of finding Intersection point of two linked lists using Floyd's Cycle Detection algorithm are:
- Use a fast pointer which moves at twice the speed as the other pointer.
- Increase the distance between the two pointers is by one at each step.
- If both the fast pointer and the slow pointer meet at some point, we have found a cycle in the list; otherwise, no cycle is present if the end of the list is reached.
3. Using difference in node counts
We can also use the difference in node counts of both lists to find the intersection point. The steps of finding Intersection point of two linked lists using difference in node counts are:
- Advance the bigger list by k nodes (where k is the difference in the number of nodes in both lists).
- Move both lists at the same speed.
- If the two lists intersect with each other, then the node at which both lists intersect is the intersection point.
4. Using distance from intersection point
It can be observed that:
The total number of nodes in the first list + distance of the head of the second list from the intersection point = The total number of nodes in the second list + distance of the head of the first list from the intersection point.
Thus, the method to find the intersection point using the distance is to take two pointers, x, which initially points to the head of the first list and y, initially pointing to the head of the second list. Then advance both pointers at the same pace until they meet at a common node. When x reaches its end, redirect it to the head of the second list. When y reaches its end, turn it to the head of the first list. The node where x and y meet would be our intersection node.
Code Implementation
Below is the code implementation of both the solutions: using recursion as well as using queue. The language of preference is C++. I have also created a Github repository that has the presented solution here as well as a solution in Python.
You can visit this link if you wish to see the repository.
1. Using hash table
#include <iostream>
#include <unordered_set>
using namespace std;
// A Linked List Node
struct Node
{
int data;
Node* next;
};
// Utility function to create a new node with the given data and
// pushes it onto the list's front
void push(Node*& headRef, int data)
{
// create a new linked list node from the heap
Node* newNode = new Node;
newNode->data = data;
newNode->next = headRef;
headRef = newNode;
}
// Function to find the intersection point of two linked lists using hashing
Node* findIntersection(Node* first, Node* second)
{
// maintain a set to store list nodes
unordered_set<Node*> nodes;
// traverse the first list and insert the address of each node into the set
while (first)
{
nodes.insert(first);
first = first->next;
}
// now traverse the second list and find the first node that is
// already present in the set
while (second)
{
// return the current node if it is found in the set
if (nodes.find(second) != nodes.end()) {
return second;
}
second = second->next;
}
// we reach here if lists do not intersect
return nullptr;
}
int main()
{
// construct the first linked list (1 —> 2 —> 3 —> 4 —> 5 —> null)
Node* first = nullptr;
for (int i = 5; i > 0; i--) {
push(first, i);
}
// construct the second linked list (1 —> 2 —> 3 —> null)
Node* second = nullptr;
for (int i = 3; i > 0; i--) {
push(second, i);
}
// link tail of the second list to the fourth node of the first list
second->next->next->next = first->next->next->next;
Node* addr = findIntersection(first, second);
if (addr) {
cout << "The intersection point is " << addr->data << endl;
}
else {
cout << "The lists do not intersect." << endl;
}
return 0;
}
2. Using Floyd’s Cycle Detection Algorithm
#include <iostream>
#include <unordered_set>
using namespace std;
// A Linked List Node
struct Node
{
int data;
Node* next;
};
// Utility function to create a new node with the given data and
// pushes it onto the list's front
void push(Node*& headRef, int data)
{
// create a new linked list node from the heap
Node* newNode = new Node;
newNode->data = data;
newNode->next = headRef;
headRef = newNode;
}
// Find the starting node of the loop in a linked list pointed by `head`.
// The `loopNode` points to one of the nodes involved in the cycle
Node* removeCycle(Node* loopNode, Node* head)
{
// find the count of nodes involved in the loop and store the count in `k`
int k = 1;
for (Node* ptr = loopNode; ptr->next != loopNode; ptr = ptr->next) {
k++;
}
// get pointer to k'th node from the head
Node* curr = head;
for (int i = 0; i < k; i++) {
curr = curr->next;
}
// simultaneously move the `head` and `curr` pointers
// at the same speed until they meet
while (curr != head)
{
curr = curr->next;
head = head->next;
}
// `curr` now points to the starting node of the loop
return curr;
}
// Function to identify a cycle in a linked list using
// Floyd’s cycle detection algorithm
Node* identifyCycle(Node* head)
{
// take two pointers – `slow` and `fast`
Node *slow = head, *fast = head;
while (fast && fast->next)
{
// move slow by one pointer
slow = slow->next;
// move fast by two pointers
fast = fast->next->next;
// if they meet any node, the linked list contains a cycle
if (slow == fast) {
return slow;
}
}
// return null if the linked list does not contain a cycle
return nullptr;
}
// Function to find the intersection point of two linked lists
Node* findIntersection(Node* first, Node* second)
{
Node* prev = nullptr; // previous pointer
Node* curr = first; // main pointer
// traverse the first list
while (curr)
{
// update the previous pointer to the current node and
// move the main pointer to the next node
prev = curr;
curr = curr->next;
}
// create a cycle in the first list
if (prev) {
prev->next = first;
}
// now get a pointer to the loop node using the second list
Node* slow = identifyCycle(second);
// find the intersection node
Node* addr = nullptr;
if (slow) {
addr = removeCycle(slow, second);
}
// remove cycle in the first list before exiting
if (prev) {
prev->next = nullptr;
}
// return the intersection node
return addr;
}
int main()
{
// construct the first linked list (1 —> 2 —> 3 —> 4 —> 5 —> null)
Node* first = nullptr;
for (int i = 7; i > 0; i--) {
push(first, i);
}
// construct the second linked list (1 —> 2 —> 3 —> null)
Node* second = nullptr;
for (int i = 3; i > 0; i--) {
push(second, i);
}
// link tail of the second list to the fourth node of the first list
second->next->next->next = first->next->next->next;
Node* addr = findIntersection(first, second);
if (addr) {
cout << "The intersection point is " << addr->data << endl;
}
else {
cout << "The lists do not intersect." << endl;
}
return 0;
}
3. Using difference in node counts
#include <iostream>
using namespace std;
// A Linked List Node
struct Node
{
int data;
Node* next;
};
// Utility function to create a new node with the given data and
// pushes it onto the list's front
void push(Node*& headRef, int data)
{
// create a new linked list node from the heap
Node* newNode = new Node;
newNode->data = data;
newNode->next = headRef;
headRef = newNode;
}
// Utility function to find the total number of nodes in a linked list
int size(Node* head)
{
int nodes = 0;
for (Node* curr = head; curr != nullptr; curr = curr->next) {
nodes++;
}
return nodes;
}
// Function to find the intersection point of two linked lists.
// Assume that the first list contains `k` nodes more than the second list
Node* findIntersection(Node* first, Node* second, int k)
{
// advance the bigger list by `k` nodes
for (int i = 0; i < k && first; i++) {
first = first->next;
}
// simultaneously move both lists at the same speed until they meet
while (first && second)
{
// if both lists meet any node, then that node is the intersection point
if (first == second) {
return first;
}
// advance both lists by one node
first = first->next;
second = second->next;
}
// return null if both lists don't meet
return nullptr;
}
// Function to find the intersection point of two linked lists
Node* findIntersection(Node* first, Node* second)
{
// get the difference in the number of nodes in both lists
int diff = size(first) - size(second);
// if the first list has a smaller number of nodes, exchange both lists
if (diff < 0) {
swap(first, second);
}
// find and return the intersection node
return findIntersection(first, second, abs(diff));
}
int main()
{
// construct the first linked list (1 —> 2 —> 3 —> 4 —> 5 —> null)
Node* first = nullptr;
for (int i = 7; i > 0; i--) {
push(first, i);
}
// construct the second linked list (1 —> 2 —> 3 —> null)
Node* second = nullptr;
for (int i = 3; i > 0; i--) {
push(second, i);
}
// link tail of the second list to the fourth node of the first list
second->next->next->next = first->next->next->next;
Node* addr = findIntersection(first, second);
if (addr) {
cout << "The intersection point is " << addr->data << endl;
}
else {
cout << "The lists do not intersect." << endl;
}
return 0;
}
4. Using distance from intersection point
#include <iostream>
using namespace std;
// A Linked List Node
struct Node
{
int data;
Node* next;
};
// Utility function to create a new node with the given data and
// pushes it onto the list's front
void push(Node*& headRef, int data)
{
// create a new linked list node from the heap
Node* newNode = new Node;
newNode->data = data;
newNode->next = headRef;
headRef = newNode;
}
// Function to find the intersection point of two linked lists
Node* findIntersection(Node* first, Node* second)
{
// Take two pointers pointing to the heads of respective lists
Node *x = first, *y = second;
// advance both pointers until they meet at a common node
while (x != y)
{
// When the first list reaches its end, redirect it to the
// head of the second list
if (x == nullptr) {
x = second;
}
else {
x = x->next;
}
// When the second list reaches its end, redirect it to the
// head of the first list
if (y == nullptr) {
y = first;
}
else {
y = y->next;
}
}
// return the common node
return x;
}
int main()
{
// construct the first linked list (1 —> 2 —> 3 —> 4 —> 5 —> null)
Node* first = nullptr;
for (int i = 7; i > 0; i--) {
push(first, i);
}
// construct the second linked list (1 —> 2 —> 3 —> null)
Node* second = nullptr;
for (int i = 3; i > 0; i--) {
push(second, i);
}
// link tail of the second list to the fourth node of the first list
second->next->next->next = first->next->next->next;
Node* addr = findIntersection(first, second);
if (addr) {
cout << "The intersection point is " << addr->data << endl;
}
else {
cout << "The lists do not intersect." << endl;
}
return 0;
}
Space and Time complexity analysis
1. Using hash table
Time Complexity: O(m + n) where m and n are the total number of elements in first and second linked lists respectively.
Space Complexity: O(m) since the algorithm stores the elements of the first linked list in a hash table.
2. Using Floyd’s Cycle Detection Algorithm
Time Complexity: O(m + n) where m and n are the total number of elements in first and second linked lists respectively.
Space Complexity: O(1) since no extra space is required to store the elements of the linked list.
3. Using difference in node counts
Time Complexity: O(m + n) where m and n are the total number of elements in first and second linked lists respectively.
Space Complexity: O(1) since no extra space is required to store the elements of the linked list.
4. Using distance from intersection point
Time Complexity: O(m + n) where m and n are the total number of elements in first and second linked lists respectively.
Space Complexity: O(1) since no extra space is required to store the elements of the linked list.
With this, you must have the complete idea of finding intersection point of two linked lists.