
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 35 minutes | Coding time: 10 minutes
Interval trees are, of course, a type of Binary Search Tree (BST) which carries different pay load then BST. By pay load, I mean node structure, or information the node stores, of the tree.
In this article, we will first see that how Interval trees differs from simple Binary Search Tree or BST. Then we will go through various Interval Tree operations such as populating the tree, searching the overlapping interval and deleting node operation. In the end, we will see python implementation and some application. So, lets get going.
Simple BST vs Interval Trees
I am assuming that you know what binary tree is and how it is structured. Just for the sake of confirmation, below image contains a simple binary tree. If you are confused, learn about Binary Search Tree (BST) by clicking here
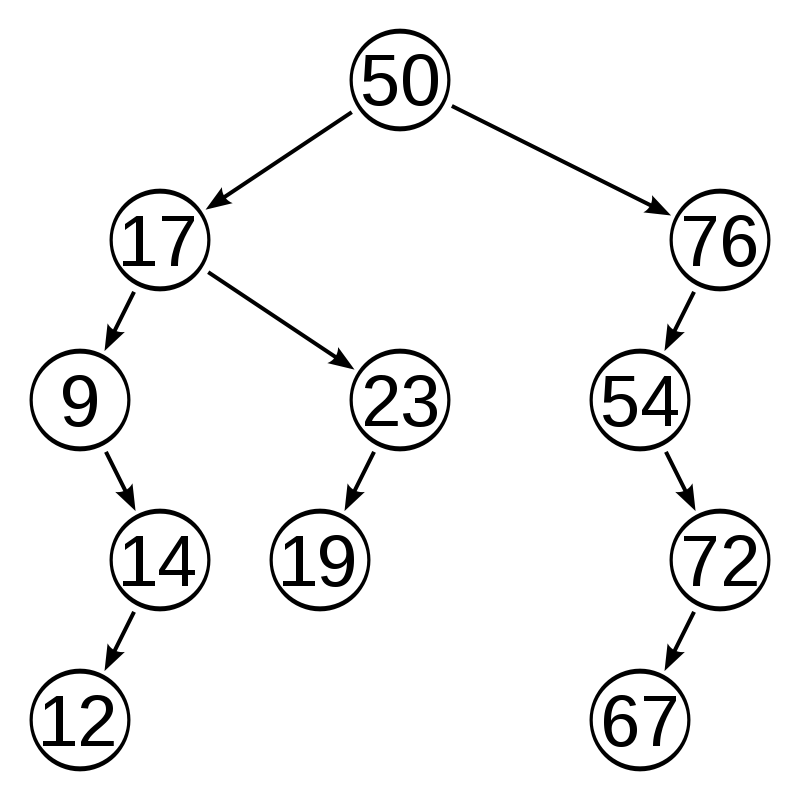
Well the tree in the image contains a balanced binary tree which means that left child of every node is smaller that the parent node and the right child is bigger. This simple rule makes our life easy when we want to some operation on it. Well how does it makes it easy? This left small and right great rule helps to keep the operation's complexity as low as possible. This is why balanced binary trees are great.
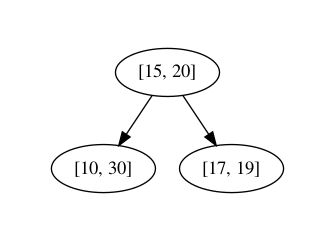
Moving on, lets get the idea of Interval tree from image below.
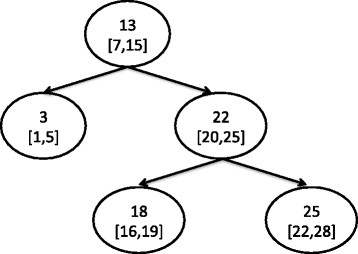
You might have observed the basic difference, that is, the node structure. Interval tree's node has an interval and also a single value which is known as max value of the sub-tree. I will explain this term later in the article.
Interval Tree - Population / Insertion O(log N)
Lets take an example to understand this. Consider this interval array,
(15, 20), (10, 30), (17, 19), (5, 20), (12, 15), (30, 40)
As usual, our first element will be the root node.
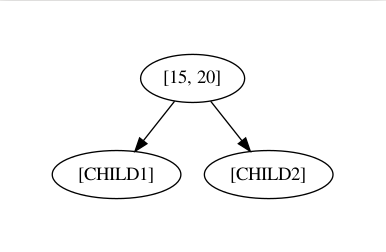
For the second element, we will compare its min value of the interval to the min value of the root node. If this min value is smaller than root node's min value than this node goes to the left of the root node or else right. So, here we have 15 and 10 where 10 is smaller than 15. So (10, 30) interval becomes left child of the root node.
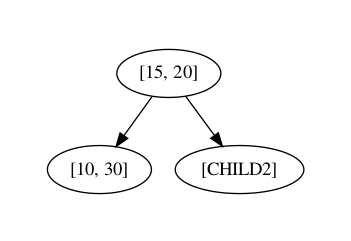
For third element (17, 19), as 17 is greater than 15 that's why this node will go on right.
For the fourth element (5, 20), 5 is smaller than 15 so we have to travel left. Now compare it will left child which is (10, 30). Of course, 5 is smaller than 10 so this node will go on the left of (10, 30). If do the same for all the remaining elements, your tree might look like this.
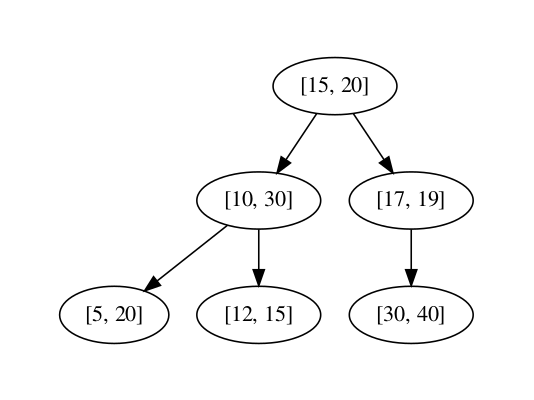
Congrats! You have successfully populated the tree. But we are missing one more component, Max value of the sub-tree. Lets see how it can be calculated for each node in our tree.
For this, we have to start with the leaves, here the leaves are (5, 20), (12, 15) and (30, 40). Starting with (5, 20), in order to find the max value of the sub-tree for this node, we have to check which is the greatest value in the sub-tree rooted with this node. Since it is a leaf, the max value will the max interval of that node. This is true of all the leaves in the tree.
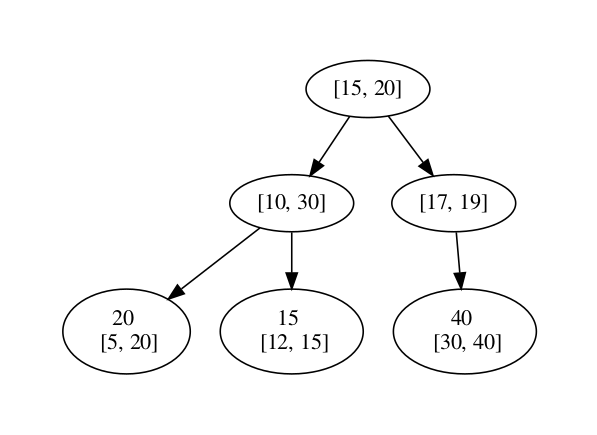
After leaves, we will start with their parents. Max value of the sub-tree at (10, 30) is the greatest number among the Max interval value at the this node, which is 30, and Max value of the sub-tree of its child node, which are 20 and 15. The greatest of all the three is 30 so that what will be the max value of the sub-tree of this node.
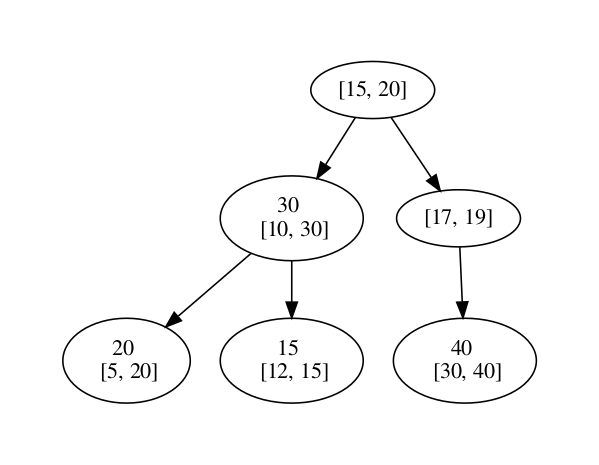
Just like that! If you continue this calculation for all the nodes, it would look like this.
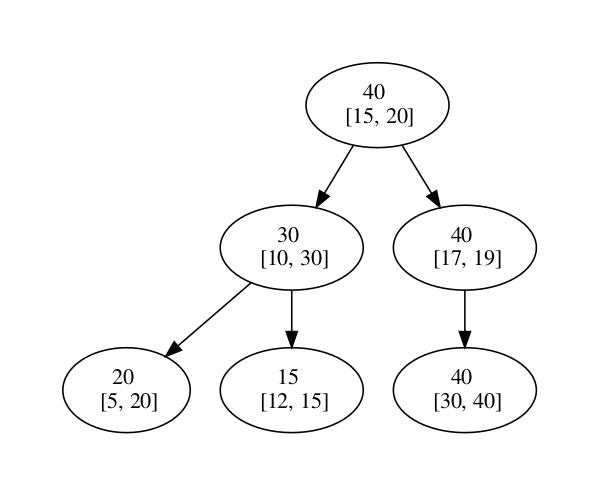
Interval Tree - Search O(log N)
Search, what we will be searching though? The answer is interval overlap. We will have interval and we need to check if there is any node in the tree which overlaps with interval of the query.
- First, we start with the root and check if there is an overlap, if it is then we will return true, if not then go ahead.
- If left child is not empty then check the max in the left child, if is greater then the query's minimum value, re-do these steps starting from left child.
- If above step does not satisfy then re-do these steps for right child.
Lets take an example, considering that we want to find the overlapping interval of (6, 7) exist in the tree.
NOTE: We will alway consider the limits of the interval inclusive.
Starting with the root node, and it does not overlap. So now will check if the min value of the query, which is 6, is greater than the Max value of the left child. Of course, 30 it is greater than 6 so we will follow the left child path.
We will check if (6, 7) overlap with the (10, 30), and it not actually so we will go for its left child and check if the max value is greater than 6. 20 is greater than 6 so we will check if there is interval overlap between the (5, 20) and (6, 7). Yay! its an overlap. The process here will return true or something positive.
Now you know how to search through the tree and find the overlap.
Deleting tree node in Interval Tree O(log N)
Earlier we saw how to insert interval node in the tree and search overlapping interval. We will discuss how to delete an overlapping interval. Start with searching for the overlap which is same as the search operation discussed above. When you find the overlapping node, check if this node has child. If no child, then simply erase the connection with its parent. But if this node has left child, then replace this node with left child with. Else, if it has only right child then replace it with it's right child.
Complication may arise if the the deleting node has both the child and they also have their own subtree. In this situation, replace the deleting node with the left child and re-insert the right child's subtree into the existing tree.
Lets start with an example, lets delete the node which intersect with [9, 11] on our old tree.
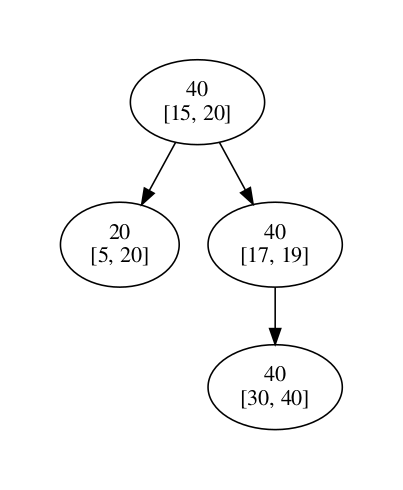
If we search our tree for the intersection, node [10, 30] will be deleted and it's place will be taken by left node, which is [5, 20].
Now we will reinsert the node [12, 15] in the tree, and our tree would look like this
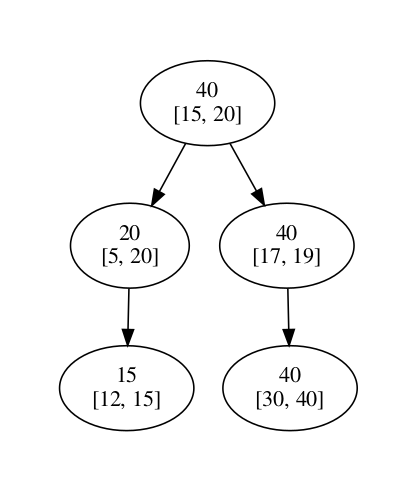
This is how you delete the node!
Python Implementation
Below is the python implementation of interval Trees from population to search.
from graphviz import Digraph # Print the tree in PDF
class Node(object):
def __init__(self, interval):
self.interval = interval
self.left_child = None
self.right_child = None
self.Max = None
def hasChild(self):
if self.left_child or self.right_child:
return True
return False
def maxOfChild(self):
child_interval = list()
if(self.left_child):
child_interval.append(self.left_child.interval)
if(self.right_child):
child_interval.append(self.right_child.interval)
return max(child_interval)
class IntervalTree(object):
def __init__(self, root):
self.root = root
def addNode(self, new_node):
node = self.root
while(node != None):
if(new_node.interval[0] <= node.interval[0]):
if(node.left_child is None):
node.left_child = new_node
return
node = node.left_child
else:
if(node.right_child is None):
node.right_child = new_node
return
node = node.right_child
def searchIntervalOverlap(self, query_node):
p_node = None
c_node = self.root
while(c_node):
if(self.isOverlapping(c_node.interval, query_node)):
print("Overlapping with ", c_node.interval)
return p_node, c_node, True
else:
p_node = c_node
if(c_node.Max >= query_node[0]):
c_node = c_node.left_child
else:
c_node = c_node.right_child
return None, None, False
def isOverlapping(self, interval_left, interval_right):
if((interval_left[0] <= interval_right[1]) and (interval_right[0] <= interval_left[1])):
return True
return False
def maxOfSubtree(self, root_node):
if((not root_node.Max) and (root_node.hasChild())):
max_array = []
if(root_node.left_child):
self.maxOfSubtree(root_node.left_child)
max_array.append(root_node.left_child.Max)
if(root_node.right_child):
self.maxOfSubtree(root_node.right_child)
max_array.append(root_node.right_child.Max)
max_array.append(root_node.interval[1])
root_node.Max = max(max_array)
return
else:
root_node.Max = root_node.interval[1]
return
def constructMax(self):
node = self.root
self.maxOfSubtree(node)
def printTree(self):
node_list = [self.root]
while(len(node_list) != 0):
current_node = node_list[0]
node_list.pop(0)
print(current_node.interval, current_node.Max)
if(current_node.left_child is not None):
node_list.append(current_node.left_child)
if(current_node.right_child is not None):
node_list.append(current_node.right_child)
return
def printTreeInPdf(self, filename):
g = Digraph('G', filename=filename)
node_list = [self.root]
while(len(node_list) != 0):
current_node = node_list[0]
node_list.pop(0)
if(current_node.left_child):
g.edge(str(current_node.Max)+"\n"+str(current_node.interval), str(current_node.left_child.Max)+"\n"+str(current_node.left_child.interval))
node_list.append(current_node.left_child)
if(current_node.right_child is not None):
g.edge(str(current_node.Max)+"\n"+str(current_node.interval), str(current_node.right_child.Max)+"\n"+str(current_node.right_child.interval))
node_list.append(current_node.right_child)
g.view()
return
def delete_node(self, node_):
parent_node, node_to_delete, _ = self.searchIntervalOverlap(node_)
# If no overlap
if not node_to_delete:
return false
if node_to_delete.hasChild():
if node_to_delete.left_child:
if self.whichChild(parent_node, node_to_delete) == "left":
parent_node.left_child = node_to_delete.left_child
else:
parent_node.right_child = node_to_delete.left_child
self.reloadTree(node_to_delete.right_child)
else:
if self.whichChild(parent_node, node_to_delete) == "left":
parent_node.left_child = node_to_delete.right_child
else:
parent_node.right_child = node_to_delete.right_child
else:
if parent_node.left_child == node_to_delete:
parent_node.left_child = None
if parent_node.right_child == node_to_delete:
parent_node.right_child = None
return True
def whichChild(self, p_node, c_node):
if p_node.left_child == c_node:
return "left"
if p_node.right_child == c_node:
return "right"
def reloadTree(self, node_):
if node_.hasChild():
if node_.left_child:
reloadTree(node_.left_child)
if node_.right_child:
reloadTree(node_.left_child)
else:
self.addNode(node_)
if __name__ == '__main__':
It = IntervalTree(Node([15, 20]))
It.addNode(Node([10, 30]))
It.addNode(Node([17, 19]))
It.addNode(Node([5, 20]))
It.addNode(Node([12, 15]))
It.addNode(Node([30, 40]))
It.constructMax()
It.printTree()
print(It.searchIntervalOverlap([6, 7])[2])
It.delete_node([9, 11])
It.printTreeInPdf("interval_tree.gv")
Complexity
Time complexity of the different operations are:
- Insertion O(log N)
- Search P(log N)
- Delete O(log N)
- Initial creation: O(N * log N) as there will be N nodes
Applications of Interval Tree
Interval trees are mostly used when dealing with geometry.
For e.g. if you want to find a point or line which is overlapping or enclosed in the rectangle, then the interval tree makes it easy to find.
Putting it more formally, Enclosing Interval Searching Problem:
Given a set S of n intervals and a query point, q, report all those intervals containing q; and Overlapping Interval Searching Problem: Given a set S of n intervals and a query interval Q, report all those intervals in S overlapping Q.
Conclusion
The good thing about the interval trees is that they have retain the search complexity, which is O(logn), from normal binary tree.
I would say the idea behind the interval tree is to maintain the self-balancing tree structure so that the search or other operation can be done in O(logn).
