
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Backtracking is one of the algorithmic techniques available for solving various constraint satisfaction problem. In this article, we will be exploring the idea of backtracking with the help of iteration (Iterative Backtracking) along with example as well. The Time and Space Complexity will be discussed at the end of the article.
Table of contents:
- Introduction to Iteration
- Advantages of Iteration
- Introduction to Backtracking
- Iterative Backtracking vs Recursive Backtracking
- Time and Space Complexity
Introduction to Iteration
Iteration is the process of repeatedly executing a set of instructions until the condition controlling the loop becomes false. It consists of initialization, comparison, statement execution within the iteration, and updating the control variable. It is crucial to have the correct controlling condition during iteration; otherwise, the program may go into an infinite loop. For example, we can use a for and while loops that runs a sequence of instructions repeatedly.
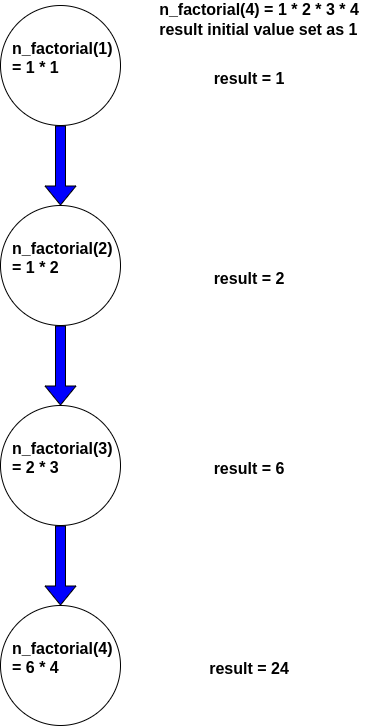
Let us look at an example which compute the n! using iteration. For example, if we set n=4 The n_factorial function will go over a for loop for the range 1 to 4.
def n_factorial(n):
result = 1
for i in range(1, n+1):
result = result * i
return result
At each iteration, the function will perform a computation by multiplying two numbers together and pass the result to the next iteration. In our example below, n = 4, at the first iteration, the result computed is 1 and this is passed to the next iteration. At the next iteration, the result computed is 2 and similarly, this result is passed to the next iteration. Next we get a result of 6. At the final iteration, the n_factorial function returned a result of 24.
Advantages of Iteration
Iteration is faster and more efficient compared to recursion. This is because iteration can be used to execute a group of statements repeatedly without the overhead of function calls or the utilization of stack memory. Infinite recursion can cause a system crash, whereas infinite repetition of Iteration just uses CPU cycles. Compared with recursion, iteration doesn't require as much memory or processing power. Iterative codes are easier to optimize and have polynomial time complexity.
Introduction to Backtracking
Backtracking is a general algorithm that does a systematic search for a solution to a specific problem among all of the potential solutions.
In backtracking, we normally start with one potential choice out of several accessible possibilities and then try to solve the problem progressively. If we are able to solve the problem with the chosen choice/move, we may simply return the solution. Otherwise, we can backtrack and pick another alternative before attempting to solve the problem. In this regard, we can consider the following:
- Find the solution to the problem, and then just return the result.
- If we exhaust all possibilities without finding a solution, we can conclude that there is no solution to the given problem.
Backtracking provides us with a lot of possibilities from which to pick. After choosing a choice, we are presented with a fresh set of possibilities. The process is repeated until we find a solution to the problem. If a solution cannot be discovered with a specific set of options/movements, we can backtrack and attempt an alternative set of options or moves. This procedure is repeated until we solve the constraint-satisfaction problems.
Let us look at the no equal adjacent substring problem and how backtracking can help us find a solution. In the example below the current string of numbers is now 01020, what number can one fill in next using 0, 1, 2 so that are no equal adjacent substring.
if X = 0, it will be in conflict with scenario A
If X = 1, it will not be in conflict with any of the scenario from A to C.
We will set X as 1 and the new string is now 010201.
A. 0102 0 X
B. 201 02 0X
C. 010 20X
As we continue to fill in the values, we come to the below scenario.
If X = 0, it will be in conflict with scenario A.
If X = 1, it will be in conflict with scenario B.
If X = 2, it will be in conflict with scenario D.
A. 010201 0 X
B. 0102 01 0X
C. 01 020 10X
D. 0102 010X
In this case, we have max out all the values that we can assign to X. We will now backtrack and try to assign a new value to X. We will start from 1 as the 0 is the previous value.
If X = 1, it will be in conflict with scenario A.
If X = 2, it will not be in conflict with any of the scenario from A to C.
We will set X as 2 and the new string is now 0102012.
A. 010201 X
B. 010 20 1X
C. 0 102 01X
If X = 0, it will not be in conflict with any of the scenario below. The string will now become 01020120
A. 010201 2 X
B. 0102 01 2X
C. 01 020 12X
D. 0102 012X
Let's take a closer look at the algorithm.
Pseudocode
def backtrack(largest_value, is_safe_function, total_slots_available):
def backtrack_from(position):
while True:
if is_safe_function(solution, position):
if position >= num_slots:
return solution
position += 1
solution[position] = 0
else:
# Backtrack
while (solution[position] == max_val):
solution[position] = None
position -= 1
if position < 0:
break
solution[position] += 1
return None if no solution
Return the solution as a list of values.
Implementation
Let us look at how we would implement the solution to our problem.
max_val- The values that we will assign to the slots will be from0tomax_val- is_safe - this refer to the
no_adjacentfunction. It will accept two arguments, solution and position. - num_slots - the total number of “slots” we want to assign values to.
- solution - the function will return the solution as a list of values.
def backtrack(max_val, is_safe, num_slots):
solution = [None] * num_slots
def backtrack_from(position):
while True:
if is_safe(solution, position):
If the values are assigned to all available slots, the function will return the solution.
if position >= num_slots-1:
return solution
position += 1
solution[position] = 0
else:
If no possible values can be assigned, we will backtrack here.
while (solution[position] == max_val-1):
solution[position] = None
position -= 1
if position < 0:
break
solution[position] += 1
If the function backtracked beyond the starting position, this meant that we could not find a valid solution.
return None
solution[0] = 0
return backtrack_from(0)
Here the function no_adjacent() check if the number satisfy the constraint, i.e. it is free of any adjacent substrings. The length of substring to test for the constraint start from 1 till half the length of the entire string. The function will return False once it found an equal adjacent pair.
def no_adjacent(string, up_to_index):
length = up_to_index+1
for j in range(1, length//2+1):
if (string[length-2*j:length-j] == string[length-j:length]):
return False
return True
Below is the driver code to print out the output of our solution.
print(''.join(str(v) for v in backtrack(3, no_adjacent, 10)))
Once u run the program, you should see the following output.
0102012021
The entire code is copied below for your reference
def backtrack(max_val, is_safe, num_slots):
solution = [None] * num_slots
def backtrack_from(position):
while True:
if is_safe(solution, position):
if position >= num_slots-1:
return solution
position += 1
solution[position] = 0
else:
while (solution[position] == max_val-1):
solution[position] = None
position -= 1
if position < 0:
break
solution[position] += 1
return None
solution[0] = 0
return backtrack_from(0)
def no_adjacent(string, up_to_index):
length = up_to_index+1
for j in range(1, length//2+1):
if (string[length-2*j:length-j] == string[length-j:length]):
return False
return True
print(''.join(str(v) for v in backtrack(3, no_adjacent, 10)))
Iterative Backtracking vs Recursive Backtracking
In iterative backtracking, we use for or while loop to solve the constraint satisfaction problem. For recursive backtracking, it use recursion to solve the problem. It may run into the insufficient memory problem due to how recursion works. Whereby it keep calling the function recursively without performing any computation. Nonetheless, recursion can yield stunningly simple answers to complicated problems.
Time and Space Complexity
Time complexity: O(N²)
There are k nested loops, the time complexity is O (N^k). In our backtrack function, k=2 as there is a loop nested within the first loop.
Space complexity: O(N).
With this article at OpenGenus, you must have the complete idea of how Iterative Backtracking help us to solve constraint satisfaction problem.
