L-Attributed and S-Attributed definitions and grammar

We have discussed two classes of definitions that can efficiently be implemented in connection to top-down or bottom-up parsing in compilers and corresponding attribute grammars that result from serious restrictions.

Table of contents.

1. Introduction.
2. S-Attributed Definitions.
3. L-Attributed Definitions.
4. L-attribute grammars.
5. S-attribute grammars.
6. Equivalence of L-attribute and S-attribute grammars.
7. Summary.
8. References.

Prerequisites.

1. Attribute Dependence Graph and Evaluation in Semantic Analysis

Introduction.

Given an SDD, it is difficult to tell whether there are any parse trees whose dependency graphs have cycles.

Here we discuss two classes of definitions that can efficiently be implemented in connection to top-down or bottom-up parsing.
We also look at attribute grammars that result from serious restrictions.
The first is the L-attribute grammar whereby an inherited attribute of a child of a non-terminal N may depend on synthesized attributes of children to the left of it in the production rule for N and on the inherited attributes of N itself.
The second is the S-attribute grammar that cannot have inherited attributes at all.

S-Attributed Definitions.

An SDD is S-attributed if every attribute is synthesized.
If an SDD is S-attributed, we evaluate its attributes in any bottom-up ordering of the parse tree nodes.
It is simpler to perform a post-order tree traversal and evaluate the attributes at a node N when the traversal leaves N for the last time.

We apply the following postorder function to the root of the tree;

postorder(N){
    for(each child C of N, from the left)
        postorder(C):
    evaluate attribute associated with node N;
}

These definitions are implemented during bottom-up parsing because a bottom-up parse corresponds to a post-order traversal, in other words, a postorder traversal corresponds to the order that an LR parser reduces the production body to its head.

L-Attributed Definitions.

The idea is that between attributes associated with a production body, the edges of a dependency graph can go from right to left but not the other way round(left to right), hence the name 'L-attributed'.

In other words, each attribute must either be;

1. Synthesized, or,
2. Inherited but with limited rules, i.e Suppose there is a production A → ${\mathrm{X}}_1$${\mathrm{X}}_2$...${\mathrm{X}}_{\mathrm{n}}$ and an inherited attribute ${\mathrm{X}}_{\mathrm{i}}$.a computed by a rule associated with this production, then the rule only uses;
   ** inherited attributes that are associated with head A.
   ** Either inherited attribute or synthesized attributes associated with the occurrences of symbols ${\mathrm{X}}_1$,${\mathrm{X}}_2$, ..., ${\mathrm{X}}_{\mathrm{i-1}}$ located to the left of ${\mathrm{X}}_{\mathrm{i}}$.
   ** Inherited or synthesized attributes that are associated with such an occurrence of ${\mathrm{X}}_{\mathrm{i}}$ itself, only in such a way that no cycles exist in the dependency graph formed by ${\mathrm{X}}_{\mathrm{i}}$ attributes.

An example:
An SDD with the following production and rules is not L-Attributed.

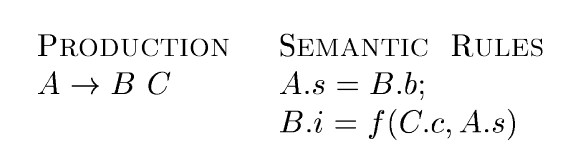
Looking at the first rule, A.s = B.b is legitimate in either an S-attributed or L-attributed SDD since it defines a synthesized attribute A.s in terms of an attribute at a child.
Looking at the second rule, it defines an inherited attribute B.i therefore, the entire SDD cannot be S-attributed since attribute C.c helps to define B.i and C is to the right of B in the body of the production.
While attributes at siblings in a parse tree may be used in L-attributed SDDs, keep in mind that they must be to the left of the symbol whose attribute is being defined.

L-attribute grammars.

During parsing, nodes are constructed from left to right, first the parent node, then the children in top-down parsing, and in bottom-up parsing, we start with the children then the parent nodes.

An L-attribute grammar allows the evaluation of attributes in one left to right traversal of the syntax tree. It is characterized by no dependency graph of any of its production rules having a data-flow edge pointing from a child to that child or to a child to its left.

Most programming language grammars are L-attributed, this is because the left to right flow of data assists programmers in reading and understanding the resulting programs.

The L-attributed property has an important consequence for processing a syntax tree in that once work starts, no part of the compiler needs to return to one of the node's siblings on the left to perform processing there.
The parser will have finished with them and their attributes already computed, only data that the nodes contain in the form of synthesized attributes remain important.

An example of data flow in part of a parse tree for an L-attributed grammar.

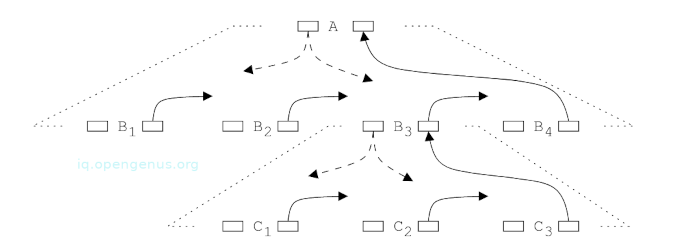
Assume an attribute evaluator is currently working on node C2 - the second child of node B3 - the third child of node A, whether A is the top or a child of another node is immaterial.
The upward arrow represents the data flow of synthesized attributes of children that all point to the right or to the synthesized attributes of the parent.

Inherited attributes are available when work on a node starts and therefore can be passed to any child that needs them. From the image, they are the ones with arrows pointing downwards.

We also see that when an evaluator is working on a node C2, two sets of attributes play a role,
The first are all attributes of the nodes lying on the path from the top to the node currently being processed: C2, B3, A.
The second are the synthesized attributes of the left siblings of those nodes: C1, B1, B2 and any left siblings of A(these are not shown).

In other words, no role is played by the children of the left siblings of C2, B3, A because all computations in them have already been performed and results summarized in their synthesized attributes, furthermore, the right siblings of C2, B3, A don't play a role since their synthesized attributes have no influence yet.

Attributes of C2, B3, A live in the corresponding nodes, work on such nodes is started but not completed. Conversely, work on their left siblings is completed.
Now, all that is left of them are their synthesized attributes

If we found a place to store data synthesized by the left siblings, we would discard each node in the left to right order after the parser has created it and the attribute evaluator has computed its attributes, meaning, we don't need to build the entire syntax tree but will always restrict ourselves to the nodes lying on the path from the top to the node being processed.

Everything remaining on the path has been processed except for synthesized attributes of the left siblings which have been discarded, everything to the right has not yet been touched.
We store the synthesized attributes in the parent node while the inherited ones remain in the nodes they belong to while their values are transported down along the path from the top to the node being processed.

S-attribute grammars.

If inherited attributes pose a problem we get rid of them and the result is an S-attribute grammar that is characterized as having no inherited attributes.
Anything that can be done with an L-attribute grammar is still possible with this grammar.

For the bottom-up parser, the complexity reduces since each node stacks its synthesized attributes, and the code at the end of an alternative of the parent scopes them all up, processes them, and replaces them with the resulting synthesized attributes of the parent.

Equivalence of L-attribute and S-attribute grammars.

It is easy to convert an L-attribute into an S-attribute grammar although this doesn't improve the looks.
The idea is to delay any computation that cannot be done now to a later occasion when it can be done.
In particular, any computation that needs inherited attributes is replaced by the creation of a data structure that specifies the computation and all its synthesized attributes up to the level where the missing inherited attributes are available as constants or as synthesized attributes of nodes at the current level, after which we perform the computation.

Transforming an L-attribute into an S-attribute grammar is attractive as it allows better bottom-up parsing methods to be implemented for more convenient attribute L-attribute grammars.
Unfortunately, this transformation is only feasible for small problems.

Summary.

In an L-attributed SDD attributes may be inherited or synthesized, this is referred to as an L-attribute definition.
In an S-attributed SDD, attributes all attributes are synthesized - S-attribute definition.

An L-attributed grammar is a grammar that node dependency graph of any of its production rules has data-flow arrow pointing from an attribute to an attribute to its left. Such grammars allow attributes to be evaluated in a left-to-right traversal.

An S-attribute grammars don't have inherited attributes at all, here attributes need to be retained only for non-terminal nodes that haven't yet been reduced to other non-terminals.
Everything that is possible with the former is possible with the latter.

References.

1. Compilers Principles, Techniques, & Tools. Chapter 5.
2. Modern Compiler Design Dick Grune, Kees van Reeuwijk, Henri E. Bal. Part II.