Leftist Heap

Reading time: 40 minutes

A node of a leftist tree contains following elements:

1. Pointer to left node
2. S-value : It is a distance to the nearest leaf
3. Data : also known as key
4. Pointer to right node

A leftist heap is a binary tree have following properties:

1. Mean Heap Property : key(parent(i)) <= key(i), i.e. the root contains the minimum key.
2. Heavy on left side : dist(right(i)) <= dist(left(i)). Here dist(i) is the number of edges on the shortest path from node i to a leaf node.

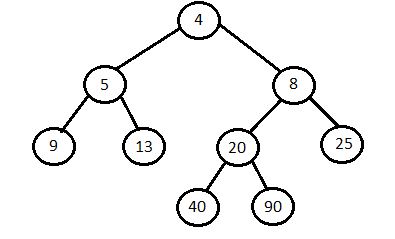
Leftist heap or Leftist tree:

Note:

• Every subtree would also be a leftist tree.
• And regarding the dist(i), it would be dist(i) = 1 + dist(right(i)).
• The path from root to the rightmost leaf would be the shortest path.

Basic Operations

1. Merge : Merge two leftist trees.
2. Insertion : Insert an element
3. Delete Minimum : Delete or extract the minimum element

Merge: O(log N)

Merge functions takes two leftist tree as input, A and B, and returns a leftist tree that contains all elements of A and B.

Pseudocode

In this pseudocode we are considering that root(A).key < root(B).key

Merge(A,B)
{
    if A = NULL
        return B;
    if B = NULL
        return A;
        
    if key(A) > key(B)
        swap A, B
    right(A) = Merge(right(A),B)
    if dist(right(A)) > dist(left(A))
        swap right(A), left(A)
    if right(A) = NULL
        dist(A) = 0
    else
        dist(A) = 1 + dist(right(A))
    return A
}

Example:

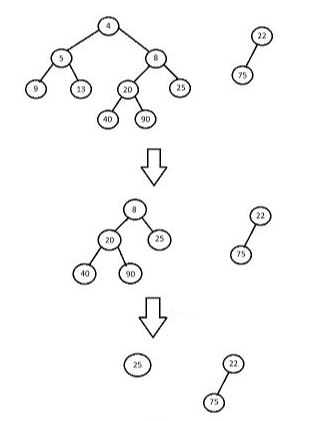
1. In this first root nodes are being compared, i.e. 4 < 22. And so 4 will be the root node of the merged leftist tree and right subtree of smallest root is used for further steps.
2. Now recursively roots are compared, so here 8 < 22. And so right subtree of root valued 8 will be considered for further steps.

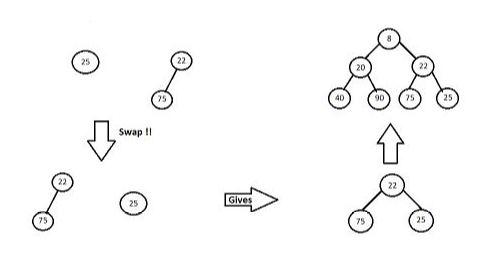
3. Here as 25 > 22. So both trees would be swapped. And after that all nodes will be merged giving 22 as root of that subtree.
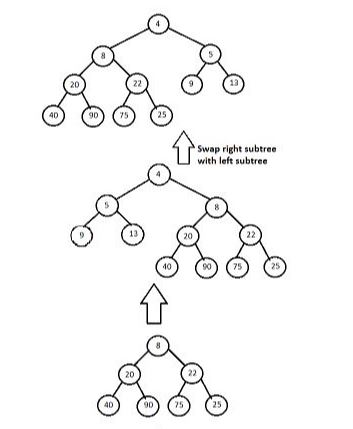
4. After that this subtree will be merged with it's previous root i.e. 8.

5. And then this subtree with root 8 will be merged with tree with root 4. But here, the obtained tree is heavier on right side.
6. So in next step right subtree and left subtree are swapped to fulfill the conditions of leftist heap.

Implementation

Implementation of merge function.

LeftistNode merge(LeftistNode * h1, LeftistNode * h2) { 
    if (h1 == NULL) 
        return h2; 
    if (h2 == NULL) 
        return h1; 
    if (h1->data < h2->data) 
        return merge1(h1, h2); 
    else
        return merge2(h2, h1); 
}

// merge1 assumes that h1's root contains smallest data.
LeftistNode merge1(LeftistNode * h1, LeftistNode * h2) { 
    if (h1->left == NULL) 
        h1->left = h2; 
    else { 
        h1->right = merge(h1->right, h2); 
        if (h1->left->dist < h1->right->dist) 
            swapChildren(h1); 
        h1->dist = h1->right->dist + 1;
    } 
    return h1; 
}

// merge2 assumes that h2's root contains smallest data.
LeftistNode merge2(LeftistNode * h2, LeftistNode * h1) { 
    if (h2->left == NULL) 
        h2->left = h1; 
    else { 
        h2->right = merge(h2->right, h1); 
        if (h2->left->dist < h2->right->dist) 
            swapChildren(h2); 
        h2->dist = h2->right->dist + 1;
    } 
    return h2; 
}

Insertion: O(log N)

Insert function will insert an element in the existing tree.
Merge Operation will be used for insertion operation.

Pseudocode

Insert(x,A){
    B <- makeATree(x)
    A <- Merge(A,B)
}

It was as simple as that.

• Just make a tree of single element x and name it B.
• And then merge it with original tree.
• As merge operation is used, this will make sure that properties of Leftist heap won't get violated during insertion.

Implementation of insert operation

Impelementation of Insert() function.

void Insert(int &x) { 
    root = Merge(new LeftistNode(x), root);      // Here "new LeftistNode()" will make a new tree of that element   
} 

Delete Minimum: O(log N)

Delete Minimum function would delete the minimum element from the tree, and that would be root. As in leftist heap the smallest element is the root of that tree.

Pseudocode

DeleteMin(A){
    x <- root.data(A)
    A <- merge(left(A),right(A))
}

• DeleteMin() can be perfmored by calling data of root.
• And then merging the left subtree and right subtree.

Implementation

Implementation of deleteMin() function

int findMin() { 
    return root->element; 
} 
  
void deleteMin() { 
    LeftistNode *oldRoot = root; 
    root = Merge(root->left, root->right); 
    delete oldRoot; 
}

Implementation

Complete Implementation including all basic operations.

#include <iostream> 
#include <cstdlib> 
using namespace std; 
  

class LeftistNode { 

    int element; 
    LeftistNode *left; 
    LeftistNode *right; 
    int dist; 
    LeftistNode(int & element, LeftistNode *lt = NULL, LeftistNode *rt = NULL, int np = 0) { 
        this->element = element; 
        right = rt; 
        left = lt, 
        dist = np; 
    } 
};
  
class LeftistHeap { 

    LeftistHeap(); 
    LeftistHeap(LeftistHeap &rhs);
    void Insert(int &x); 
    void deleteMin(); 
    void Merge(LeftistHeap &rhs); 
 
    LeftistNode *root; 
    LeftistNode *Merge(LeftistNode *h1, 
                       LeftistNode *h2); 
    LeftistNode *Merge1(LeftistNode *h1, 
                        LeftistNode *h2); 
    void swapChildren(LeftistNode * t);
}; 
  

LeftistHeap() { 
    root = NULL; 
} 
  

LeftistHeap(LeftistHeap &rhs) { 
    root = NULL; 
    *this = rhs; 
} 

void Merge(LeftistHeap &rhs) 
{ 
    if (this == &rhs) 
        return; 
    root = Merge(root, rhs.root); 
    rhs.root = NULL; 
} 
  

LeftistNode Merge(LeftistNode * h1, LeftistNode * h2) { 
    if (h1 == NULL) 
        return h2; 
    if (h2 == NULL) 
        return h1; 
    if (h1->element < h2->element) 
        return Merge1(h1, h2); 
    else
        return Merge1(h2, h1); 
} 
  

LeftistNode Merge1(LeftistNode * h1, LeftistNode * h2) { 
    if (h1->left == NULL) 
        h1->left = h2; 
    else { 
        h1->right = Merge(h1->right, h2); 
        if (h1->left->dist < h1->right->dist) 
            swapChildren(h1); 
        h1->dist = h1->right->dist + 1; 
    } 
    return h1; 
} 
  
void swapChildren(LeftistNode * t) 
{ 
    LeftistNode *tmp = t->left; 
    t->left = t->right; 
    t->right = tmp; 
} 
  
void Insert(int &x) { 
    root = Merge(new LeftistNode(x), root); 
} 
  
int findMin() { 
    return root->element; 
} 
  
void deleteMin() { 
    LeftistNode *oldRoot = root; 
    root = Merge(root->left, root->right); 
    delete oldRoot; 
} 
  
bool isEmpty() { 
    return root == NULL; 
} 
  
bool isFull() { 
    return false; 
} 
  
  
int main() { 
    LeftistHeap h; 
    LeftistHeap h1; 
    LeftistHeap h2; 
    int x; 
    int arr[]= {5, 8, 10, 15, 18}; 
    int arr1[]= {6, 12}; 
  
    h.Insert(arr[0]); 
    h.Insert(arr[1]); 
    h.Insert(arr[2]); 
    h.Insert(arr[3]); 
    h.Insert(arr[4]); 
    h1.Insert(arr1[0]); 
    h1.Insert(arr1[1]); 
  
    h.deleteMin(x); 
    cout<< x << "\n"; 
  
    h1.deleteMin(x); 
    cout<< x << "\n"; 
  
    h.Merge(h1); 
    h2 = h; 
  
    h2.deleteMin(x); 
    cout<< x << "\n"; 
  
    return 0; 
} 

Complexity

1. Merge : O(log N)
2. Insert : O(log N)
3. deleteMin : O(log N)
4. getMin : O(1), beacuse fetching of root can be done in O(1).

Applications

• Solving problems like find min/max element in efficient time.
• Solving problems like find kth min/max element in efficient time.