
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have disccussed two approaches (recursive + iterative) to solve the problem "Letter Combinations of a Phone Number" in C++ language with explanation of Time and Space complexity.
Table of contents:
1.Explanation of the problem
2.Recursive approach discussion
- Approach discussion
- Algorithm walkthrough
- Implementation of recursive code
- Time and space complexity
3.Iterative approach discussion
- Approach discussion
- Algorithm walkthrough
- Implementation of Iterative code
- Time and space complexity
Prerequisite: Recursion
This is similar to Leetcode problem 17. Letter Combinations of a Phone Number.
Explanation of the problem
Given an string containing digits from [0, 9], the task is to print all possible letter combinations that the number could represent.
we know in dial-pad we don't have any letters associated with 0 and 1 so ignore them and Map all other digit to letters (just like dial-pad) in given image below.
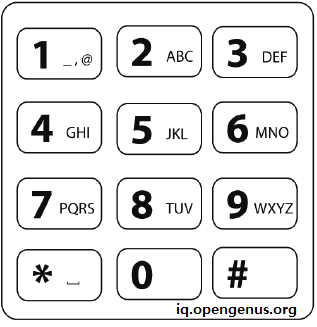
Input number: 347
Output:
dgp dgq dgr dgs dhp dhq dhr dhs dip diq dir dis
egp egq egr egs ehp ehq ehr ehs eip eiq eir eis
fgp fgq fgr fgs fhp fhq fhr fhs fip fiq fir fis
Explanation: look at the number
given as input which starts with "3" where we know in
phone dial-pad button digit 3 offers us three choices d e and f and digit 4 offers us g h and i and 7 offers us p, q, r, and s.so we try to print all the possible formation of a word by choosing each button once in alphabetical order.
Input number: 6
Output: m n o
Explanation: In this example, if we look closely for each word formation
we are only allowed to press it ones so we will be getting all the letters of 6
in alphabetical order.
Recursive approach discussion
APPROACH DISCUSSION
- It is observed that each digit represents either 3 tor 4 different alphabets leaving 0 and 1.
- Now we see that we are given just the string as input, and the expected output is the formation of words with the letters corresponding to the given string indices. so, how about we map all the number(string indices) with the corresponding letters offered by those numbers on the dial-pad.
- Now the idea is to try recursion where the recursive function will try all the alphabets, mapped to the current digit in alphabetic order, and again call the recursive function for the next digit and will pass on the current output string.
ALGORITHM
- Map the numbers with a string of probable alphabets.
- Create a helper recursive function with parameters passed as input string, empty string to store output string, index which is initially 0, and length of the string.
- Now we know if recursion is there then there has to be a base case so in this case if the current_index is equal to the length of the string then print the output string, because we get to choose only one letter at a time from a given digit.
- Extract each letter of the input string one by one.
- Run a loop to traverse the string from start to end
- and now for every index again call the recursive function with the output string concatenated with the ith character of the string and the current_index + 1.
IMPLEMENTATION
class Solution {
public:
vector<char> keypad[10] =
{
{}, {}, // 0 and 1 digit don't have any characters associated
{ 'a', 'b', 'c' },
{ 'd', 'e', 'f' },
{ 'g', 'h', 'i' },
{ 'j', 'k', 'l' },
{ 'm', 'n', 'o' },
{ 'p', 'q', 'r', 's'},
{ 't', 'u', 'v' },
{ 'w', 'x', 'y', 'z'}
};
vector<string> ans;
void helper(string digits, string res, int index, int n)
{
// base case
if(index==n)
{
ans.push_back(res);
return;
}
// getting digit one by one
int curr_digit = int(digits[index]-'0');
// no of alphabets present in the corresponding curr_digit
int len = keypad[curr_digit].size();
for(int i=0;i<len;i++)
{
helper(digits,res+keypad[curr_digit][i],index+1,n);
}
}
vector<string> letterCombinations(string digits) {
// base case
// if the string is empty
int n =digits.size();
if(n==0)
return ans;
// input string , curr_string which is empty , index from which we start
// and length of the string
helper(digits,"",0,n);
return ans;
}
};
OUTPUT
INPUT -"234"
OUTPUT -["adg","adh","adi","aeg","aeh","aei","afg","afh","afi","bdg","bdh","bdi","beg","beh","bei","bfg","bfh","bfi","cdg","cdh","cdi","ceg","ceh","cei","cfg","cfh","cfi"]
TIME COMPLEXITY
O(4N), where N is a length of the input string.
Each digit of corresponds to 3 or 4 letter, hence can be said that each digit might have 4 choices. If the length of string is n digits and in worst case all the digits of the string have 4 alpahabets to offer than for the first digit and for each alphabet of the first digit there are 4 options in the second digit, i.e for every recursion 4 more recursions are called till it hits the base case. So the time complexity is O(4N).
SPACE COMPLEXITY
we are not using any extra space so it is O(1).
Iterative approach discussion
APPROACH DISCUSSION
- whenever we talk about switching from recursive to iterative one thing is observed that it reduces time complexity and increases space complexity.
- So as mentioned in the above point increase in space complexity, means additional data structure.
- In terms of logic it would be the same as recursive but instead of recursion call we would be storing it in data structure and returning it at the end.
- We can choose DFS as well as BFS traversal to form all the words but what DFS does is forms a string one by one whereas in the case of BFS it starts forming all the strings together like after n passes(n-> length of the string) it will have
all the possible string formation. - Here, we would choose BFS traversal specifically because we do need all the strings but in a lexicographical order which can be possible with data structure queue used in BFS traversal.
ALGORITHM
- Map the numbers with a string of probable alphabets.
- Maintain a queue.
- Push an empty string in it.
- Now check for a condition if the queue is empty or not. get the first string pushed
- Base case here would also be the length of the input string
- Now get the currdigit as the index of the string
- Try all possible letters for the current digit on the keypad and push it into the queue.
IMPLEMENTATION
class Solution {
public:
vector<char> keypad[10] =
{
{}, {}, // 0 and 1 digit don't have any characters associated
{ 'a', 'b', 'c' },
{ 'd', 'e', 'f' },
{ 'g', 'h', 'i' },
{ 'j', 'k', 'l' },
{ 'm', 'n', 'o' },
{ 'p', 'q', 'r', 's'},
{ 't', 'u', 'v' },
{ 'w', 'x', 'y', 'z'}
};
vector<string> ans;
void helper(string digits, int n)
{
queue<string> q; // mainatin a queue
q.push(""); // empty string is pushed
while(q.empty()==false)
{
auto x =q.front();
q.pop();
// base case
if(x.size()==n)
{
ans.push_back(x);
}
else
{
int digit = int(digits[x.size()]-'0'); // current index of string
// Trying all possible letters for current digit in keypad
for(auto letter: keypad[digit])
{
q.push(x+letter);
}
}
}
}
vector<string> letterCombinations(string digits) {
// base case
// if the string is empty
int n =digits.size();
if(n==0)
return ans;
// input string , curr_string which is empty , index from which we start
// and length of the string
helper(digits,n);
return ans;
}
};
};
OUTPUT
INPUT -"234"
OUTPUT -["adg","adh","adi","aeg","aeh","aei","afg","afh","afi","bdg","bdh","bdi","beg","beh","bei","bfg","bfh","bfi","cdg","cdh","cdi","ceg","ceh","cei","cfg","cfh","cfi"]
TIME COMPLEXITY
O(4N)
The iterative approach is same as the recursive version. The only difference is that in the iterative approach, we are using maintaining an explicit queue instead of using System Stack. The iterative approach is preferred as you have more memory control and prevents Stack Overflow errors of Recursive approach.
SPACE COMPLEXITY
We are using extra space of a queue O(N) (where N is the length of the string).
With this article at OpenGenus, you must have the complete idea of solving the problem Letter Combinations of a Phone Number.
