Given a string, we are required to find the longest palindromic substring.A substring is a contiguous sequence of characters within a string. For example, in the string "minor", "in", "ino", "min",...etc are substrings, but not "mr". Whereas palindrome is a word that reads the same backwards as forwards. Examples include abba, aaaa, hannah.

Consider a string "babad", the longest palindromic substring is "bab". However, "aba" is also a valid answer.
Similarly
aabac --> aba
gogogh--> gogog

Note in the above example ogo is also a palindrome but gogog is the longest one.

There are many approaches to solve this problem like dynamic programing, palindromic tree, Manacher's algorithm and so on. In this article we will see how to solve this program in two ways:

1. Brute Force
2. Dynamic Programming

Brute Force

When given a string, and asked to find the longest palindromic substring, a nested approach that considers every substring and individually checks if it is a palindrome is an idea that would definitely strike. It is a time consuming O(n^3) approach.

The implementation is given below.

Brute force Implementation

#include<bits/stdc++.h>
using namespace std;

bool isPalindrome(string s){
int low=0, high=s.size()-1;
while(low<=high){
if(s[low] != s[high]) 
  return false;
low++;
high--;
}
return true;

}

int main(){
string s = "babad";
int maxCount = INT_MIN;
string res;
for(int i = 0; i < s.size(); i++) {
    for(int j = i; j < s.size(); j++) {
        string temp = s.substr(i, j-i+1);
            if(isPalindrome(temp) && temp.size() > maxCount) {
                maxCount = temp.size();
                res=temp;
            }
    }
  }
 cout<<res;
 return 0;
}

Output

bab

Why the algorithm works and it's drawbacks

The algorithm might seem very simple, we run two loops i, from 0 to the size of the string, and j that starts from i. This is because we are not counting the substrings from backwards. The string function substr() is used to extract the substring starting from i, and j-i+1 characters. We check if this string is a palindrome or not, the isPalindrome is a very basic function. We also have a maxCount that stores the length of the longest substring. If a given string is palindrome and this length is greater than maxCount we update the values of maxCount and make res, which is the longest palindromic substring, to temp.

O(n^3) is a bad time complexity. We can make this better. There are some observations we can make here

1. Every individual character of a string is a palindrome
   Therefore, there is no need of calling the isPalindrome() method every time for this.
2. We don't need a isPalindrome() for a string with two characters
   For example consider str = "ab", we don't require a loop for this, when we can simply find out if str[0] and str[1] are equal or not.
3. Strings with size greater than 2
   For string size 3 we can check if str[0] and str[2] are equal that's it.
   For strings greater than this size, we need information regarding the strings of lesser sizes. This suggests an optimal substructure where an optimal solution can be constructed from optimal solutions of sub-problems.

We can store these results in an array. This suggests the use of dynamic programming.

Dynamic Programing

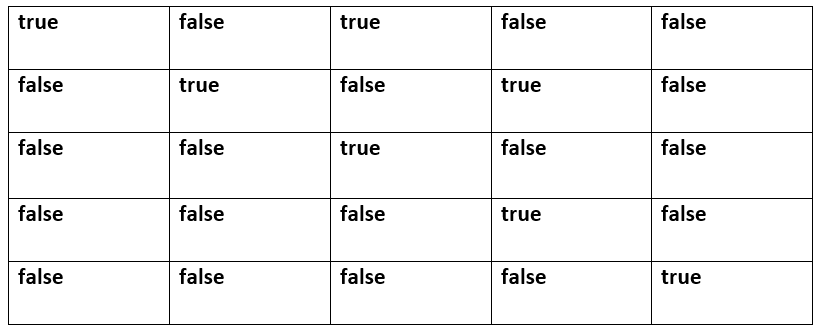
From the information above, we need a memoisation table. Therefore we use a 2D boolean array where the rows represent i, and columns represent j. Let's call this array dp[][], and dp[i][j] will store whether the substring from ith position to jth is a palindrome or not. The table will be initialized to false.

dp[i][j] = whether the substring from index i to j is a palindrome or not

For example consider string "babad" dp[2][4] is false because the substring(2,4) "bad" is not a palindrome.

We will completely remove the isPalindrome(), instead we write simple logic to fill the table. The same nested loop will be here, but the logic is changed the logic can be explained as:

Case 1:

i==j
Every single character of a string is a palindrome. Therefore dp[i][j] is true.

Case 2:

j-i=1
We're checking two characters at a time, if s[i]==s[j], then dp[i][j] is true.

Case 3:

j-i>=2
Consider "aba" s[0]=s[2], therefore dp[i][j] will be true. If s[i]==s[j], but j-i>=2, dp[i][j] = dp[i+1][j-1]. Now the i+1,j-1 coordinates are literally eliminating the first and last character, since they are already the same, we want to know if the string without them is still a palindrome or no? This result will in turn be any of the above cases or this case, nevertheless, the result has already been calculated.

Dynamic Programming Implementation

#include<bits/stdc++.h>
using namespace std;

int main(){
string s = "babad";
int n = s.size();
     
bool dp[n][n];
memset(dp, false, sizeof(dp));
int x,y,max=INT_MIN;
        
for(int i=n-1; i>=0; i--){
     for(int j=i; j<=n-1; j++){
          if(i==j)
               dp[i][j] = true;
          else if(s[i] == s[j]){
             if(j-i == 1) dp[i][j]=true;
              else
                dp[i][j] = dp[i+1][j-1];
            }
          if(dp[i][j] && j-i>=max){
               max=j-i;
                x=i;
                y=j;
            }
        }
    }
    
    cout<<s.substr(x,y-x+1);
    return 0;
}

Output

bab

In addition to the above cases, we have included the max variable that stores the length of the longest palindromic substring, we also have x and y that stores pointers to the first and the last characters of the longest palindromic substring. Other than the core logic, we've also changed the loop, though it traverses backwards, we are counting the substrings forward only. The memoisation table would look like.

The dynamic programing approach gives us a time complexity and auxiliary space complexity of O(n^2). The time is better than the previous one, but, the space isn't.

Applications

1. The approach explained here can be applicable to many dynamic programming questions directly like longest common subsequence(LCS) etc.

2. The dynamic programming approach is very useful when it comes to optimization problems like the graph algorithms(All pair shortest path algorithm) that are extensively applied in real-life systems.

With this article at OpenGenus, you will have the complete idea of using Dynamic Programming for finding the longest palindromic substring. Enjoy.