Find path with maximum average value in a 2D matrix

Given a square matrix of size N * N, where each cell is associated with a specific cost. Find the path with maximum average value in the 2D matrix. The path should start from top left point and end at bottom right point with possible movements being right and down only. Average is computed as total cost divided by the number of cells visited in the path.

We have explored 3 approaches to solve this and Dynamic Programming is one of the efficient approaches.

Example:

Input : matrix = [9, 8, 7
                  6, 5, 4
                  3, 2, 1]
Output : 5.8
Explanation : Path with maximum average is, 9 -> 8 -> 7 -> 4 -> 1

Intuition

• As the only allowed moves are down and right, we need N-1 down moves and N-1 right moves to reach the destination (bottom rightmost).
• So any path from top left corner to bottom right corner requires 2N – 1 cells.
• In average value, the denominator is fixed and we need to just maximize numerator.
• Therefore we basically need to find the maximum sum path.

Approach 1 : Brute Force

• The Brute Force algorithm is a simple recursive algorithm.
• From each cell first print all paths by going down and then print all paths by going right.
• Do this recursively for each cell encountered.
• Count the path sum of each of the path.
• Return the max value out of all the path sums.
• Find the avetage value by dividing it with (2 * n) - 1.

/* mat:  the input matrix 
   i, j: Current position (For the first call use 0,0) 
   n: Dimentions of given the matrix 
   pi:   Next index to be filed in path array 
   path[0..pi-1]: The path traversed till now (Array to hold the 
                  path need to have space for at least 2n elements)
   sums: Array containing the whole path length sum for each path
 */
void sumAllPathsHelper(vector<vector<int>> &mat, int i, int j, int n, vector<int> &path, int pi,vector<int> &sums) 
{ 
    // Reached the bottom of the matrix so we are left with 
    // only option to move right 
    if (i == n - 1) 
    { 
        for (int k = j; k < n; k++) 
            path[pi + k - j] = mat[i][k];
        int cur_path_sum;
        for (int l = 0; l < pi + n - j; l++) 
            {
                cur_path_sum+=path[l]; 
            }
        sums.push_back(cur_path_sum);
        return; 
    } 
  
    // Reached the right corner of the matrix we are left with 
    // only the downward movement. 
    if (j == n - 1) 
    { 
        for (int k = i; k < n; k++) 
            path[pi + k - i] = mat[k][j]; 
        int cur_path_sum;
        for (int l = 0; l < pi + n - j; l++) 
            {
                cur_path_sum+=path[l]; 
            }
        sums.push_back(cur_path_sum);
        return; 
    } 
  
    // Add the current cell to the path being generated 
    path[pi] = mat[i][j]; 
  
    // sum all the paths that are possible after moving down 
    sumAllPathsHelper(mat, i+1, j, n, path, pi + 1, sums); 
  
    // sum all the paths that are possible after moving right 
    sumAllPathsHelper(mat, i, j+1, n, path, pi + 1, sums); 
    
} 
// The main function that prints all paths from top left to bottom right 
// in a matrix 'mat' of size n x n 
int max_path_avg (vector<vector<int>> &mat,int n) 
{ 
    vector<int> path (2*n);
    vector<int> sums;
    sumAllPathsHelper(mat, 0, 0, n, path, 0, sums);
    double path_sum_max_val= *max_element(sums.begin(), sums.end());
    return (path_sum_max_val)/(2*n-1);
}

• The time complexity of above solution is exponential.

Approach 2 : Recursion

For each element, we consider two paths, rightwards and downwards and find the maximum sum out of those two. It specifies whether we need to take a right step or downward step to maximize the sum.

cost(i,j)=matrix[i][j] + max(cost(i+1,j),cost(i,j+1))

where cost(i,j) represents maximum sum of the path from the index (i, j) to the bottom rightmost element.

vector<int> calculate(vector<vector<int>> matrix, int i, int j) {
        if (i == matrix.size() || j == matrix[0].size()) 
                return INT_MIN;
        if (i == matrix.size() - 1 && j == matrix[0].size() - 1) 
                return matrix[i][j];
        return matrix[i][j] + max(calculate(matrix, i + 1, j), calculate(matrix, i, j + 1));
}
    double max_Average(vector<vector<int>> matrix) {
        int max_path_sum= calculate(matrix, 0, 0);
        int n= matrix.size();
        double avg_val= (double)max_path_sum/(2n-1);
        return avg_val;
    }

Time complexity : O(2^(2n)). For every move, we have atmost 2 options.
Space complexity : O(2n). Recursion of depth 2n.

To reduce the time complexity from exponential value, we can use Dynamic Programming approach to solve this problem. It is more efficient than both brute force approach and the recursive one.

Approach 3 : Dynamic Programming

• We use an extra matrix dp of the same size as the original matrix.
• In this matrix, dp(i, j) represents the maximum sum of the path from the index (i, j) to the top leftmost element.
• We start by initializing the top leftmost element of dp as the first element of the given matrix.
• Then for each element starting from the top left, we traverse forwards and fill in the matrix with the required maximum sums.
• Now, we need to note that at every element, we can move either rightwards or downwards.
• Therefore, for filling in the maximum sum, we use the equation:

dp(i, j) = matrix(i,j) + max(dp(i-1,j),dp(i,j-1))

while taking care of the boundary conditions (3 in this case).

Here, for each element in the input matrix, we compute the maximum sum of the path from the index (i, j) to the top leftmost element in form of dp(i,j) by adding the current element value with maximum of the 2 path sums i.e. maximum sum of the path till it's upper element dp((i-1),j) and its left element dp((i-1),j).

Algorithm

Algorithm ( array matrix[][] , number of elements in a single row/column in array or n )
{
    create dp array of size [n+1][n+1] 
    
    set the top leftmost element of dp array dp[0][0] with the same of matrix array matrix[0][0] 
    (1st boundary condition)
    
    for all j, 1 <= j <= N     (2nd boundary condition)
       set dp[0][j] = dp[0][j-1] + matrix[0][j]; 
       
       
    for all i, 1 <= i <= N     (3rd boundary condition)
       set dp[i][0] = dp[i-1][0] + matrix[i][0];  
    
    otherwise for all other elements of dp array    
       set dp[i][j] = matrix[i][j] + max(dp[i-1][j], dp[i][j-1]); 
    
    divide maximum sum by constant path length : (2N - 1) for getting average 
    i.e. (double)dp[n-1][n-1] / (2*n-1)
    
    return the above average
}

Execution :

Starting from the below array input.

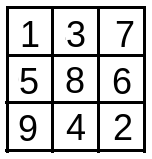
dp array is formed of size (n,n) i.e. dp[3][3].

The 1st row 1st element of dp is dp[0][1] is formed as below :

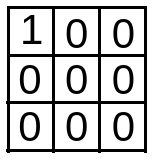
The 1st row 2nd element of dp is formed as below :

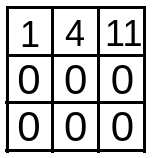
The 1st column 2nd element of dp is formed as below :

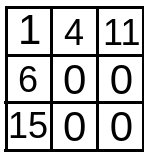
Iteration starts from 2nd index onwards i.e. i = 1 till i < n or i < 3. In each iteration, subsequent rows of dp array are filled.

In the 1st iteration (i = 1),

Then for j = 1 till n-1 (here 1 till 2), dp[i][j] is updated.

• when j = 1 , dp[i][j] = max(dp[i-1][j],dp[i][j-1]) + matrix[i][j] i.e. max(dp[0][1],dp[1][0]) + matrix[1][1] = max(4,6) + 8 . So, dp[i][j] i.e. dp[1][1] = 6 + 8 = 14 .
• when j = 2 , dp[i][j] = max(dp[i-1][j],dp[i][j-1]) + matrix[i][j] i.e. max(dp[0][2],dp[1][1]) + matrix[1][2] = max(11,14) + 6 . So, dp[i][j] i.e. dp[1][2] = 14 + 6 = 20 .

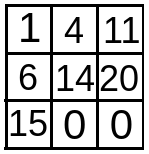
In the 2nd iteration (i = 2),

Then for j = 1 till n-1 (here 1 till 2), dp[i][j] is updated.

• when j = 1 , dp[i][j] = max(dp[i-1][j],dp[i][j-1]) + matrix[i][j] i.e. max(dp[1][1],dp[2][0]) + matrix[2][1] = max(14,15) + 4 . So, dp[i][j] i.e. dp[2][1] = 15 + 4 = 19 .
• when j = 2 , dp[i][j] = max(dp[i-1][j],dp[i][j-1]) + matrix[i][j] i.e. max(dp[1][2],dp[2][1]) + matrix[2][2] = max(20,19) + 2 . So, dp[i][j] i.e. dp[2][2] = 20 + 2 = 22 .

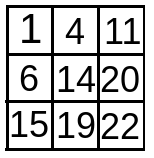
• With i=3, outer iteration ends.

For finding the maximum average value ,the maximum value of dp array found at dp[n-1][n-1] i.e. dp[2][2] is divided with constant path length : (2n - 1) or 5.

So, the output is 22/5 = 4.4.
Path with maximum average is, 1 -> 5 -> 8 -> 6 -> 2

Implementation Code :

#include <bits/stdc++.h> 
using namespace std; 

// method returns maximum average of all path of cost matrix 
double max_Average(vector<vector<int>> matrix, int n) 
{ 

	int dp[n][n]; 
	dp[0][0] = matrix[0][0]; 

	/* Initialize first row of dp array */
	for (int j = 1; j < n; j++) 
		dp[0][j] = dp[0][j-1] + matrix[0][j]; 

	/* Initialize first column of dp array which calculates total cost*/
	for (int i = 1; i < n; i++) 
		dp[i][0] = dp[i-1][0] + matrix[i][0]; 
       
    /* Construct rest of the dp array */
	for (int i = 1; i < n; i++) 
		for (int j = 1; j < n; j++) 
			dp[i][j] = matrix[i][j] + max(dp[i-1][j], 
						dp[i][j-1]); 

	// divide maximum sum by constant path length : (2N - 1) for getting average 
    double g = (double)dp[n-1][n-1] / (2*n-1);
	return g; 
    
} 

/* Driver program  */

int main() 
{ 
	vector<vector<int> > matrix;
    cout<<"Enter the size of the matrix"<<endl;
    int n,a;
    cin>>n;
    matrix.resize(n);
    for(int i=0;i<n;i++){
        matrix[i].resize(n);
        for(int j=0;j<n;j++){
            cin>>a;
            matrix[i][j]=a;
        }   
    }
    double b=max_Average(matrix, n);
	cout<<b; 
	return 0; 
} 

Input :

[ 1, 3, 7
  5, 8, 6
  9, 4, 2 ]

Output :

4.4

Time & Space Complexity

Time complexity for the above approach is O(N * N) where N is the number of elements in a single row/column of the 2D matrix.

Space complexity for the above approach is O(N * N) where N is the number of elements in a single row/column of the 2D matrix, for the max_Average function which makes the dp array.