Reading time: 35 minutes | Coding time: 15 minutes

The problem statement is similar to the "Rod Cutting problem", unlike finding the maximum revenue by adding up the prices of different lengths, we find the maximum product of length of individual pieces of the rod, of given length 'n'. Just like the previous one, we have are given a rod of length 'n' we are required to cut the rod in such a way that their product (of the length) is maximum. We can assume that the rod of length 'i' has price 'i' associated with it.

The problem statement emphasizes on the term "maximum" that takes us through the path of any optimization problem, to "Dynamic Programming". Let's see the detailed explanation of the problem statement with example, followed by the approaches to solve the problem.

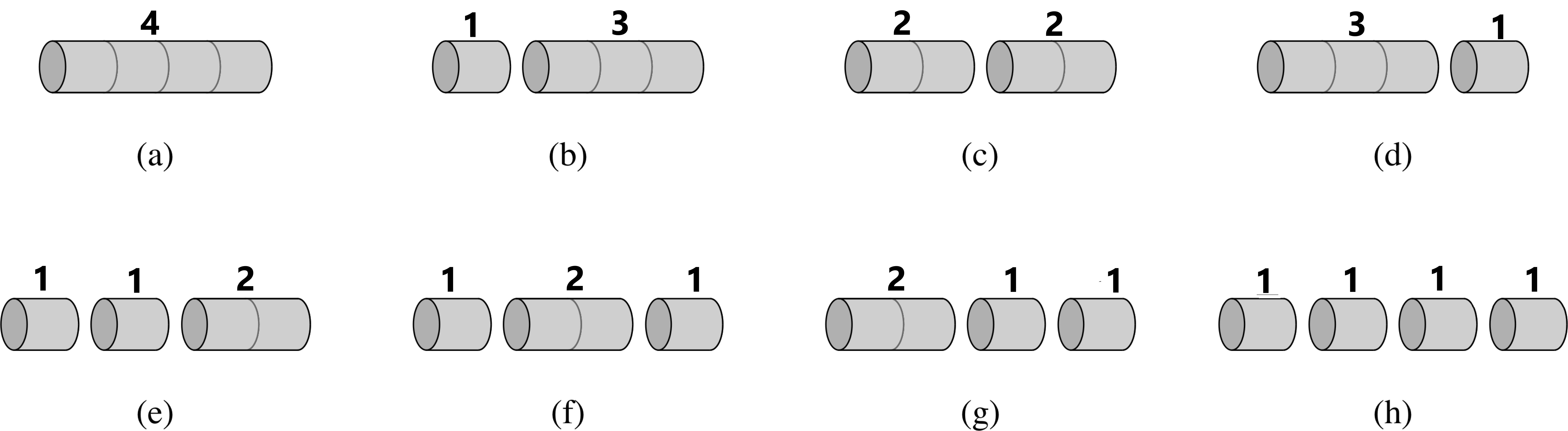
The above figure depicts 8 possible ways of cutting up rod of length 4. Above each piece is given the price of that piece according to the table. The optimal way of cutting the rod is c since it gives maximum revenue(4).

For n=5
The number of ways to cut the rod are 2^(n-1) ways to cut it, since we make n-1 cuts for any rod of length 'n'. For rod size 5, we have 2^(4) ways i.e 16 ways to cut it.

Cut	Profit
5	5
1,4	4
1,1,3	3
1,3,1	3
3,1,1	3
1,1,1,2	2
1,1,2,1	2
1,2,1,1	2
2,1,1,1	2
1,1,1,1,1	1
2,1,2	4
2,2,1	4
1,2,2	2
2,3	6
3,2	6
4,1	4

We have taken two approaches to solve this problem

1. Brute Force
2. Dynamic Programming

Brute Force approach

As we've seen for a rod of length 'n' there are 2^(n-1) ways to cut it. And since the price of size i is i itself, to get optimal result we need to consider three calculations and determine the maximum among them.

max_val = max(max_val, (n-i)*i, maxProd(n-i)*i)

For rod length of 5, we started calculating from (1,4), the max_val makes a comparison among the previous max_val, (1*4), maxProd(4)*1.
The maxProd(4) gives the optimal result i.e maximum product for the rod length 4, and by doing this we can understand if calling that method gives an optimal result or not.

The code for the above approach is given below

#include<iostream>
using namespace std;

int max(int a, int b){
  return (a>b)? a:b;
}
int max(int a, int b, int c){
  return max( max(a,b), c);
}
 
int maxProd(int n){
    if(n==0 || n==1) 
        return 0;
    int max_val=0;
    for(int i=1; i<n; i++){
        max_val = max(max_val ,(n-i)*i ,maxProd(n-i)*i);
    }
    return max_val;
}
 
int main(){
  cout<<"Maximum Product for rod length 5 is "<<maxProd(5);
return 0;
}

Output:

Maximum Product for rod length 5 is 6

What the algorithm does?

We've written basic code to find the maximum value among three numbers. In the function maxProd, we've taken max_val as our maximum product that we are returning. Unlike our previous problem i.e rod cutting problem, we've initialized max_val to be 0, as we know that the price of the rod being its length itself, we can't have a rod with negative price, hence the initialization.
For every iteration we consider two options whether to make a cut or no, either ways we calculate the result and find the maximum product.

max_val = max(max_val ,(n-i)*i ,maxProd(n-i)*i);

We've basically partitioned the rod of length 'n' into i and (n-i) for all i in {1,2.....n-1} and call the function for (n-i) as this would give us the optimal result of cutting the rod of length (n-i). We multiply this recursive result with the current i to get an overall optimal result. Therefore we pick up the maximum from these two values and the previous max_val. And just like below figure illustrates, our algorithm is a top down one, we run the loop till the rod length and return the max_val.

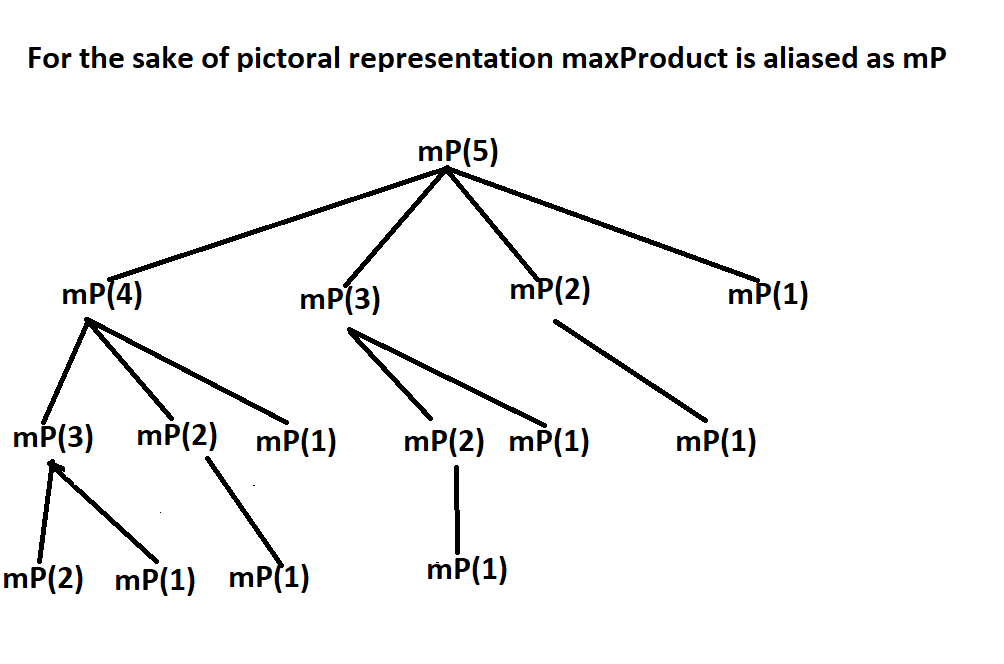
For the calculation of max_val, the function follows a top down approach and calls itself several times, most of it being redundant. We can see that mP(1) has been computed 7 times.

Although in hindsight the algorithm looks pretty linear, when we run it, due to excessively calling itself again and again, it forms a tree kind of structure, metaphorically.

Therefore the time complexity is O(2^n)

Here's where Dynamic Programming steps in

Dynamic Programing approach

1) Optimal Substructure

To solve a optimization problem using dynamic programming, we must first characterize the structure of an optimal solution. Specifically, we must prove that we can create an optimal solution to a problem using optimal solutions to subproblems. We can’t really use dynamic programming if the optimal solution to a problem might not require subproblem solutions to be optimal. This often happens when the subproblems are not independent of each other.
For cutting the rod of length 4, we considered cutting it into 2,2 would be optimal. Even for the 2 we choose, there are optimal ways to cut that as well. (We can store all these intermediate results)

2) Overlapping Subproblems

For dynamic programming to be useful, the recursive algorithm should require us to compute optimal solutions to the same subproblems over and over again, because in this case, we benefit from just computing them once and then using the results later. In total, there should be a small number of distinct subproblems (i.e. polynomial in the input size), even if there is an exponential number of total subproblems.

An array is used to store the intermediate results. However the idea of solving the problem remains the same.
We use the same logic of the brute force solution, but we are solving the problem using dynamic programming by adding an array thereby storing the intermediate results without having to recursively call the function again and again.

max_val = max(max_val ,(n-i)*i ,maxProd(n-i)*i);

The above logic can be modified as

max_val = max(max_val, j*val[i-j], j*(i-j));

The entire code is given below

#include<iostream>
using namespace std;

int max(int a, int b){
  return (a>b)? a:b;
 }
int max(int a, int b, int c){
  return max( max(a,b), c);
  }
 
int maxProd(int n){
int val[n+1];
val[1]=1;
for(int i=2; i<n+1; i++){
  int max_val = INT_MIN;
  for(int j=1; j<i; j++){
   max_val = max(max_val, val[i-j]*j, (i-j)*j);
   }
 val[i]=max_val;
}
return val[n];
}
 
int main(){
  cout<<"Maximum Product for rod length 5 is "<<maxProd(5);
return 0;
}

Output:

Maximum Product for rod length 5 is 6

What the algorithm does?

When applying dynamic programming, we calculate or fill the array in a bottom-up fashion and one of the table value (the last value, mostly) will be the result.
In our case we took val[] as the memoisation table and val[n] being the answer.

In the beginning of our code, we wrote the basic logic to calculate maximum when given three values. And of course this function called another maximum function(same name, but different number of parameters(Function Overloading)) that calculates maximum of two numbers. Indeed, we can skip both the functions and write our code as

max_val = max(max_val , max((i-j)*j, val[i-j]*j));

The max() here is a pre-defined function that is present in the <algorithm> header of the C++ library. All we need to do is simply include it.

The crucial function here is maxProd() that calculates the maximum product obtained after the cutting the rope. We take val[] as our table, with it's size being n+1. Now you may doubt why n+1. We took it in order to avoid any array out of bound situations. val[1] is initialized to 1 as that's the base case.

For maxProd(5) the memoisation table would look like

i	val[i]
1	1
2	1
3	2
4	4
5	6

To ensure optimal substructure, the i loop calculates the optimal product for rod of ith value. And the j loop assists this process by considering all the values i.e partitioning for a given rod of length 'i', which is 1,2....i-1. And for the overlapping subproblems we store the values in val[].

For this purpose, we start our i loop from 2, take a temporary variable max_val and set to the least integer possible, and calculate the optimal result in the j loop and assign this max_val to val[i].

At the end we return val[n].

For maxProd(5)
val[1]=1
base condition, for rod length that's the maximum product we can get.
val[2]=1
we consider (1,1)
val[3]=2
we consider maximum of (1,1,1), (1,2). Hence the answer.
val[4]=4
we consider maximum of (1,1,1,1), (2,2), (1,2,1) , (1,3).
val[5]=6
all the possibilities of cutting the rod of length 5 has been given above.

This algorithm yields a computational complexity of O(n^2). The complexity has evidently improved since the last brute force one, due to dynamic programing.

Applications

1. The approach explained here can be applicable to many dynamic programming questions directly like the fibonacci series, and indirectly be used to understand other questions like coin change problem, longest common subsequence(LCS) etc.
2. The dynamic programming approach is very useful when it comes to optimization problems like the graph algorithms(All pair shortest path algorithm) that are extensively applied in real-life systems.
3. The others include 0/1 knapsack problem, Mathematical optimization problem, Reliability design problem, Flight control and robotics control, Time sharing: It schedules the job to maximize CPU usage.

Although this problem and the rod cutting one seems similar in a way where we are required to cut the rod of given length in different sizes and find an optimal value, there are some notable differences such as:

Rod Cutting Problem

• The prices of various rod lengths when cut are given
• The problem requires to find maximum revenue by adding up the prices of such a rod when cut.
• The time complexity of brute force solution is O(2^(n-1))

Maximum product cutting problem

• We are not given any prices, we assume our prices to be i
• We are required to find maximum product by multiplying the prices of such a rod
• Time complexity of the brute force solution is O(2^n)